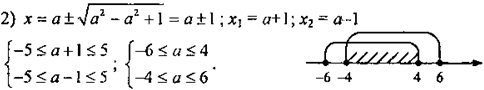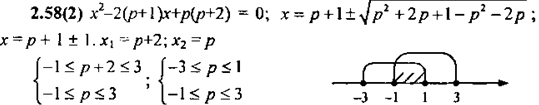Разделы: Математика
Цель:
- формировать умение распознавать положение квадратной параболы на плоскости в зависимости от параметра,
- развивать логическое мышление,
- умение работать в проблемной ситуации.
Ход урока
Проверка домашнего задания.
Объяснение нового материала.
Решение многих задач с параметрами, предлагаемых на экзаменах, в частности, на ЕГЭ по математике, требует умения правильно формулировать необходимые и достаточные условия, соответствующие различным случаям расположения корней квадратного трёхчлена на числовой оси.
Пусть квадратный трёхчлен f(x) = ax 2 + bx + с имеет корни x1 и x2, 
— абсцисса вершины параболы y = ax 2 + bx + с, d — заданное число. Рассмотрим ряд утверждений, связанных с взаимным расположением x1 , x2 и числа d.
Теорема 1. Для того чтобы оба корня квадратного трёхчлена были больше числа d, (рис.1) необходимо и достаточно выполнение условий.
Пример:
При каких значениях параметра а корни уравнения ax 2 —(2а + 1)х + 3а — 1 = 0 больше единицы?
Решение: 1. При а = 0 х = -1 — не удовлетворяет требованию задачи.
2. При а 
Ответ: 
Теорема 2. Для того чтобы оба корня квадратного трёхчлена были меньше числа d, (рис.2) необходимо и достаточно выполнение условий
Рассмотрим задачи на применение этих теорем, обращая внимание на алгоритм получения необходимых и достаточных условий, соответствующих данному случаю расположения корней квадратного трёхчлена на числовой оси. Учащиеся должны научиться составлять эти условия, а не пытаться механически их запомнить.
Задачи для самостоятельного решения.
Найдите значение параметра m, при которых уравнение 
имеет два отрицательных решения.
Ответ: при 
уравнение имеет два отрицательных решения.
Найти все значения параметра 
, при которых уравнение 
имеет два положительных различных решения.
Ответ: при 
уравнение имеет два положительных различных решения
При каких значениях параметра а корни уравнения 
больше 1?
Ответ: при 
корни уравнения больше 1.
При каких значениях параметра а оба корня уравнения 
меньше 1?
Ответ: при 
оба корня уравнения меньше 1.
При каких значениях параметра p оба корня квадратного трехчлена 
отрицательны?
Ответ: при 
оба корня квадратного трехчлена отрицательны.
Найдите все значения параметра а, при которых оба корня уравнения 
больше 1?
Ответ: не существует таких значений параметра а, при которых оба корня уравнения больше 1.
Теорема 3. Для того чтобы число d было расположено между корнями квадратного трёхчлена, (рис.3) необходимо и достаточно выполнение условий
Задача для самостоятельного решения
Найти все значения параметра 
, при которых только один корень квадратного трехчлена 
больше 2.
Ответ: 
или 
.
При каком значении параметра 
один корень уравнения 
больше 1, а другой — меньше 1?
Ответ: при 
один корень уравнения больше 1, а другой — меньше 1.
При каких значениях параметра 
число 2 находится между корнями квадратного уравнения 
?
Ответ: при 
один корень уравнения больше 2, а другой — меньше .
Найти все значения параметра 
, при которых только один корень уравнения 
удовлетворяет неравенству 
.
Ответ: 
или 
.
Теорема 4. Для того чтобы оба корня квадратного трёхчлена лежали в интервале (d: p), (рис.4) необходимо и достаточно выполнение условий
(4)
Пример. При каких значениях параметра а оба корня уравнения удовлетворяют условию 1 8.08.2010
Видео:Корни уравнения с параметромСкачать
Раздел II. № 2.58. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. При каких значениях р корни уравнения принадлежат промежутку?
1) При каких значениях а корни уравнения
х 2 -2ах + (а + 1)(а — 1) = 0
принадлежат промежутку [-5; 5]?
2) При каких значениях р корни уравнения
х 2 -2(р + 1)х + р(р + 2) = 0
принадлежат промежутку [-1; 3]?
(1) х 2 -2ах+(а+1)(а-1) = 0
1) x 2 -2ах+a 2 -1 = 0
Ответ: при -4 ≤ а ≤ 4 .
Ответ: при -1 ≤ р ≤ 1.
Видео:Нахождение корней уравнения, принадлежащих промежуткуСкачать
Квадратные уравнения с параметром
Уравнение называется квадратным, если имеет вид (ax^2+bx+c=0,) где (a,b,c) — любые числа ((a≠0)). При этом надо быть внимательным, если (a=0), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при (x^2) и рассматривать 2 случая: (a=0) (линейное уравнение); (a≠0) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Исследование квадратного многочлена
Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:
- Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа (γ): (x_1≤x_2 0)); ветки параболы направлены вниз ((a 0). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число (γ) должно по условию лежать вне отрезка ((x_1,x_2)), то (f(γ)>0).
- (a 0). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа (γ).
В итоге получаем:
если (a*f(γ) 0), то (γ∉(x_1,x_2)).
Нам осталось наложить условие, чтобы наши корни были слева от числа (γ). Здесь нужно просто сравнить положение вершины нашей параболы (x_0) относительно (γ). Заметим, что вершина лежит между точками (x_1) и (x_2). Если (x_0 0, \x_0 
При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?
1 случай: Если (a(a+3)=0), то уравнение будет линейным. При (a=0) исходное уравнение превращается в (6x-9=0), корень которого (x=1,5). Таким образом, при (a=0) уравнение имеет один корень.
При (a=-3) получаем (0*x^2+0*x-0=0), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.
2 случай: Если (a≠0; a≠-3), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-frac.$$ С учетом (a≠0;) (a≠-3), получим, что уравнение имеет два корня при (a∈(-frac;0)∪(0;+∞)). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):
Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку ([-2;2]).
1 случай: Если (a=-1), то (0*x^2-x+1-1=0) отсюда (x=0). Это решение принадлежит ([-2;2]).
2 случай: При (a≠-1), получаем квадратное уравнение, с условием, что все корни принадлежат ([-2;2]). Для решения введем функцию (f(x)=(a+1) x^2-(a^2+2a)x-a-1) и запишем систему, которая задает требуемые условия:
Подставляем полученные выражения в систему:
📽️ Видео
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
Отбор корней по окружностиСкачать
При каких значениях параметра уравнение имеет единственный кореньСкачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
найти при каких значениях параметра А уравнение будет иметь только 1 корень.Скачать
Параметр | При каких значениях параметра решение неравенства принадлежит отрезку| Задача 17 ЕГЭ 2022Скачать
Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать
Отбор корней по окружностиСкачать
Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать
✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать
896 Алгебра 8 класс При каких значениях а уравнение Квадратное имеет 2 корня принадлежащиеСкачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
961 Алгебра 8 класс . При каких значениях уравнение имеет два корня принадлежащие интервалуСкачать
5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать
