Найду корень уравнения: (3-p)x2+7x+9-p2=0
Решение
Дано линейное уравнение:
Раскрываем скобочки в левой части ур-ния
Приводим подобные слагаемые в левой части ур-ния:
Переносим свободные слагаемые (без x)
из левой части в правую, получим:
$$- p_ + 7 x + x_ left(3 — pright) = -9$$
Переносим слагаемые с другими переменными
из левой части в правую, получим:
$$7 x + x_ left(3 — pright) = p_ + -9$$
Разделим обе части ур-ния на (7*x + x2*(3 — p))/x
Получим ответ: x = -9/7 — 3*x2/7 + p2/7 + p*x2/7
Видео:При каких значениях параметра уравнение имеет единственный кореньСкачать
Алгебра. 8 класс
Укажите все правильные ответы.
Выберите приведённые квадратные уравнения.
Укажите правильный ответ.
При каких значениях p уравнение 
будет неполным квадратным уравнением?
Впишите верный ответ.
Решите уравнение 
.
Если уравнение имеет более одного корня, то в ответе укажите сумму корней.
Впишите верный ответ.
Решите уравнение 
.
Если уравнение имеет более одного корня, то в ответе укажите произведение корней.
Заполните пропуски в тексте.
1) В уравнении 
первый коэффициент равен ,
второй коэффициент равен , свободный член равен .
2) В уравнении 
первый коэффициент равен ,
второй коэффициент равен , свободный член равен .
3) В уравнении 
первый коэффициент равен ,
второй коэффициент равен , свободный член равен .
Установите соответствие между квадратными уравнениями и их решениями.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
Неполные квадратные уравнения
теория по математике 📈 уравнения
Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax 2 +c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Пример №1. Решить уравнение:
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:
Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax 2 +bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
Обе части уравнения делим на (–14) и получаем х 2 =0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:
Также делим обе части на 23 и получаем х 2 =0. Значит, корень уравнения – нуль.
🎬 Видео
6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать
№5 Неполное квадратное уравнение х^2-3x=0 Как разложить на множители Вынести х за скобку Как решитьСкачать
Уравнения с параметром. Алгебра, 8 классСкачать
Решить квадратное уравнение с параметром - bezbotvyСкачать
Математика | Параметр. Система уравнений с параметромСкачать
ЕГЭ по математике // Задание 5, 7 // Неполное квадратное уравнениеСкачать
Уравнение с параметром | Математика TutorOnlineСкачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Когда алгебраическая дробь равна 0?Скачать
Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать
Сможешь решить уравнение с параметром? Что делать с модулем и при чем тут гипербола?Скачать
СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать
Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезкеСкачать
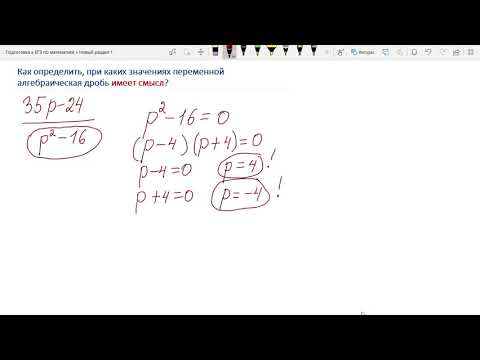
Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать
Собственные значения и функции p-Лапласа (Владимир Бобков)Скачать
Как найти значения переменной, при которых алгебраическая дробь не имеет смысла?Скачать
