При каких значениях m оба корня уравнения равны нулю

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

При каких значениях m оба корня уравнения равны нулю

Раз оба корня равны нули, значит они равные. А равные корни могут быть только при дискриминанте D=0.

D=b^2-4ac a=1,b=-a^2-3a,c=3a-a^2 D=0

Так и оставляем дискиминант.

Теперь проверяем, удолетворяет ли найденные нами a решению уравнения с параметром. Для этого подставим их в уравнение дискриминанта:

Видео:При каких значениях параметра уравнение имеет единственный кореньСкачать

При каких значениях m ровно один из корней уравнения равен нулю : 3x ^ 2 + x + 2m — 3 = 0?

Алгебра | 5 — 9 классы

При каких значениях m ровно один из корней уравнения равен нулю : 3x ^ 2 + x + 2m — 3 = 0.

Подставим вместо «x» ноль и уравнение превратится в линейное :

3 * 0 + 0 + 2m — 3 = 0

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

РЕШИТЕ УРАВНЕНИЕ ПО АЛГЕБРЕ RX + 23 = 0 ЕСЛИ R НЕ РАВЕН НУЛЮ?

РЕШИТЕ УРАВНЕНИЕ ПО АЛГЕБРЕ RX + 23 = 0 ЕСЛИ R НЕ РАВЕН НУЛЮ.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Помогите пожалуйста?

Алгебра 9 класс

У меня в решении корней нет, я думаю тут какой — то подвох.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Алгебра, 9 класс Найти сумму корней уравнения?

Алгебра, 9 класс Найти сумму корней уравнения.

Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

При каких значениях m один из корней уравнения x ^ 2 — 3x + m ^ 2 — 4 = 0 равен нулю?

При каких значениях m один из корней уравнения x ^ 2 — 3x + m ^ 2 — 4 = 0 равен нулю?

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

ПОМОГИТЕ ПОЖАЛУЙСТА АЛГЕБРА 8 КЛАСС КВАДРАТНЫЕ УРАВНЕНИЯ?

ПОМОГИТЕ ПОЖАЛУЙСТА АЛГЕБРА 8 КЛАСС КВАДРАТНЫЕ УРАВНЕНИЯ.

Видео:Когда алгебраическая дробь равна 0?Скачать

При каких значениях переменной равно нулю значение трехчлена — p ^ 4 + p ^ 2 — 0, 25?

При каких значениях переменной равно нулю значение трехчлена — p ^ 4 + p ^ 2 — 0, 25.

Помогите пожалуйста, Алгебра 8 класс.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

8 класс?

1. При каком значении к сумма корней кв.

Уравнения равна 0?

В уравнении() квадрат разности корней равен 16.

При каком значении параметра m сумма квадратов корней уравнения наибольшая?

4 . найти сумму квадратов всех корней уравнения

При каких значениях p и q корни уравнения равны 2p и

помогите, а то не врубаюсь в эту чепуху.

Видео:Как определить, при каких значениях переменной алгебраическая дробь имеет смысл?Скачать

И с этим пожалуйста помогите, просто в алгебре нуль?

И с этим пожалуйста помогите, просто в алгебре нуль.

Видео:Уравнения и задачи с одной неизвестной. Тема№ 3 Теорема Виета и обратная ей теорема.Скачать

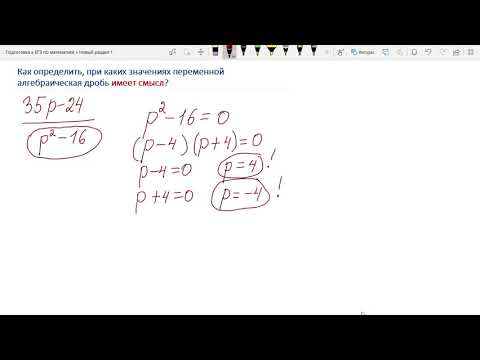
При каком отрицательном значении а уравнение имеет ровно два корня?

При каком отрицательном значении а уравнение имеет ровно два корня?

Тема : применение производной для исследования функций на монотонность и экстремумы, 10 класс.

Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Помогите с алгеброй пожалуйста, СРОЧНО?

Помогите с алгеброй пожалуйста, СРОЧНО!

Найти сумму корней.

На этой странице сайта вы найдете ответы на вопрос При каких значениях m ровно один из корней уравнения равен нулю : 3x ^ 2 + x + 2m — 3 = 0?, относящийся к категории Алгебра. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Пусть I сторона = х, тогда II = 3x, а III = (3x — 1). Зная, что периметр — сумма длин всех сторон, составим и решим уравнение : 3х + х + (3х — 1) = 34 7х = 35 х = 5 3х = 15 3х — 1 = 14.

1) 13а — 2bc + 19bc = 13a + 17bc ; 2) 0, 7b² + 20a + 2b² = 20a + 2, 7b² ; 3) 9, 3c + 4, 5d³ — 5, 1d³ = 9, 3c — 0, 6d³ ; 4) 10nm + 9x — 20nm = — 10nm + 9х ; 5) 5xy — 34xy + 3, 3a = 3, 3a — 29xy ; 6) 0, 8t⁴ + 2, 4c — 2, 1t⁴ = 2, 4c — 1, 3t⁴.

Видео:Неполное квадратное уравнение. Модуль. Параметр.Скачать

Методическая разработка урока на тему «Неполные квадратные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Неполные квадратные уравнения и их решение

Определение. Квадратным уравнением называется уравнение вида

Числа а, b и с называются коэффициентами квадратного уравнения. Число а называют первым коэффициентом, число b – вторым коэффициентом, а число с – свободным членом.

Наиболее простыми для решения являются квадратные уравнения, в которых коэффициенты b или с равны нулю. Такие уравнения называют неполными квадратными уравнениями. К их числу относятся, например, уравнения: 5 х ² + 3 х = 0; -4 х ² + 12 = 0; 2 х ² = 0. В первом из них с = 0 и b ≠ 0,

во втором b = 0и с ≠ 0, в третьем с = 0 и b = 0. Эти уравнения представляют различные виды неполных квадратных уравнений, отличающихся способом решения. Рассмотрим по порядку решения всех этих видов уравнений.

Уравнение примет вид:

А) если коэффициенты а и с – числа одного знака, то выражение – отрицательное и уравнение не имеет решений;

Б) если коэффициенты а и с – числа разных знаков, то выражение – положительное и уравнение имеет два решения

1.Если, то уравнение имеет два корня, равных по модулю, но разных по знаку.

2. Если, то уравнение не имеет корней .

Уравнение примет вид:

Решение: разложим левую часть уравнения на множители

получим х=0 или а х + b = 0

Уравнение имеет два корня, один из которых равен 0, а другой x = —

Уравнение примет вид:

ах² = 0, откуда х² =0, х=0

Уравнение имеет только один корень, равный 0

Задание 1. Расположите данные уравнения и таблицу, в зависимости от количества корней уравнения:

1)5х² + 6х = 0; 2) — х² = 0; 3) -0,3х² + 9 = 0; 4) -0,1х² + 5х = 0;

5) 0,6х² + 12 =0; 6) -4х² = 0; 7) -0,3х² — 6 =0; 8); х² — = 0;

9) х² + 6х = 0 ; 10) 7х² — 49 = 0; 11) 2х² = 0; 12)

Уравнение имеет два корня,

один из которых равен 0.

Пример 1 . Решить уравнение

Пример 2. Решить уравнение

Пример 3. Решить уравнение

Пример 4 . Решить уравнение

А) Решите уравнение 5х² — 10 = 0. Если корней несколько, найдите их произведение.

Б) Укажите уравнение, которое не имеет корней.

В) найдите корни уравнения (х+1)² — 1+2х=0

Г) Какие из уравнений имеют иррациональные корни:

Пример 5 . При каком значении параметра m уравнение является неполным квадратным: а) б)

а) Запишем уравнение в виде . Выпишем коэффициенты данного квадратного уравнения : а = -1, b = 5 m ² — 20, c =1. Коэффициент с не может быть равными нулю, следовательно, уравнение будет неполным квадратным при условии b =0,т.е. если 5 m ² — 20=0. Откуда m = ±4.

Ответ: m = -4, m = 4.

б) Выпишем коэффициенты данного квадратного уравнения: а =, b = -3,

c = m ²+ m . Если коэффициент а=0, то квадратное уравнение обращается в линейное, следовательно коэффициент а ≠0, т. е. m +1≠0, следовательно

m ≠ -1. Данное уравнение будет неполным квадратным при условии с=0, т.е.

откуда m =0 или m = -1. Но выше мы выяснили, что m ≠ -1. Значит нашему условию удовлетворяет только m =0/

Рассмотрим примеры, в которых нужно определить, при каких значениях параметра квадратные уравнения имеют корни :

равные по модулю, но различные по знаку,

только один из корней, равный нулю,

только один корень, равный нулю.

Случай 1) выполняется при условии, что в квадратном уравнении коэффициент b =0

Следует различать задания 2) и 3). В задании 2) уравнение имеет два корня, при этом только один из них равен 0, а в задании 3) уравнение имеет только один корень; при этом он равен 0. Или еще говорят , что уравнение имеет два равных корня, каждый из которых равен нулю.

Пример 6. При каких значениях m ровно один из корней уравнения

2х ² — mx + 2 m ² — 3 m = 0 равен нулю ?

Решение. Следует различать условия, при которых уравнение имеет только один корень, равный нулю ( если b =0 и с = 0) и условия, при которых уравнение имеет один из корней равен нулю ( с=0). В данном уравнении мы будем рассматривать второй случай, т.е. когда с = 0. В данном уравнении

а =2, b = — m , c = 2 m ²-3 m . Итак, запишем условие 2 m ² — 3 m = 0, m (2 m -3) = 0, m = 0 или m =1,5.

Если m = 0, то получим уравнение 2х²=0. А это уравнение имеет только один корень, равный нулю, что не соответствует нашему условию.

Если m =1,5, то получим уравнение 2х² -1,5х+ 21,5² — 31,5 = 0, т.е

2х² — 1,5х=0. Корни этого уравнения х=0, х=0,75. С ледовательно нашему условию удовлетворяет только m =1,5.

Ответ : при m =1,5.

Пример 7. При каких m уравнение 4 x ²+(5| m |-1) x + 3 m ² + m =0 имеет корни, равные по модулю, но разные по знаку?

Решение . Выпишем коэффициенты данного уравнения: а = 4, b = 3| m |-1,

c = 6 m ² + m . Уравнение имеет корни, равные по модулю, но разные по знаку при условии, что коэффициент b = 0, т.е. 3| m |-1=0; 5| m | = 1; | m | = ; m = или m = — .

1) Если m = — , то получим уравнение 4 x ² — = 0. Это уравнение имеет два корня х= х=.

2) Если m = , то получим уравнение 4 x ² + = 0, которое не имеет корней, т.к. коэффициенты а и с – числа одного знака.

Пример 8 . При каких значениях m уравнение 8 x ²-(3 m ²+4 m ) x +9 m ² — 16 = 0 имеет только один корень, равный нулю?

Решение . Выпишем коэффициенты данного уравнения: а = 8, b = 3 m ²+4 m ,

c = 9 m ² -16. Уравнение имеет только один корень, равный нулю при условии, что коэффициенты с = 0 и b = 0 одновременно. С=0, если

9 m ² -16 = 0 ,т.е. если m = ± .

Если m = , то коэффициент b = 3 m ²+4 m ≠ 0, а значит получим уравнение , не удовлетворяющее нашему условию.

Если m = — , то коэффициент b = 3 m ²+4 m = 0, и данное уравнение примет вид 8х² = 0, которое имеет только один корень, равный нулю.

Задание. 1. При каких значениях m ровно один из корней уравнения

Решение . Уравнение имеет один из корней равен нулю, если ____________________, т.е. если m = 3, m =_____.

1)Если m = 3, то уравнение примет вид_______________. А это уравнение имеет ______________________________ , что не соответствует нашему условию.

2)Если m = ____ , то получим уравнение____________________,

Корни этого уравнения_______________________. Следовательно нашему условию удовлетворяет только m = _______.

Выпишем коэффициенты данного уравнения: ___________________________________________.

Уравнение имеет корни, равные по модулю, но разные по знаку при условии, ______________, т.е.____________________________________________;

1) Если m = _______ , то получим уравнение_________________. Это уравнение имеет _______________________________________________

2) Если m = , то получим уравнение 3 x ² +1 = 0, которое ___________________, т.к. коэффициенты а и с – числа_________________.

Следовательно нашему условию удовлетворяет только m = _______.

Выпишем коэффициенты данного уравнения: ___________________________. Уравнение имеет только один корень, равный нулю при условии, что коэффициенты _________________________________________________. С=0, если __________________________________________________________

1)Если m = 1 , то коэффициент b =________, и данное уравнение примет вид_____________, которое имеет только один корень, равный нулю

2)Если m = _____ , то коэффициент b _____________, а значит получим уравнение _______________________, которое имеет _________________.

Ответ: при m = _______.

При каких значениях m ровно один из корней уравнения

При каких m уравнение +имеет корни, равные по модулю, но разные по знаку?

При каких значениях m уравнение 5 x ²- ( m -6) x +36- m ² = 0 имеет только один корень, равный нулю?

🎬 Видео

При каких значениях параметра k 0 находится между корнями уравненияСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать