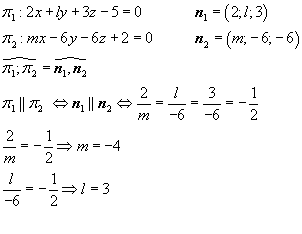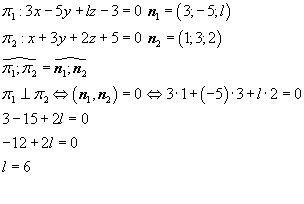При каких значениях и уравнения и будут определять параллельные плоскости

1. Определить, при каких значениях и следующие пары уравнений будут определять параллельные плоскости: 1) 2x+ly+3z-5=0, mx-6y-6z+2=0; 2) 3x-y+lz-9=0, 2x+my+2z-3=0;

(Ответ: )

2. Определить двугранные углы, образованные пересечением следующих пар плоскостей: 1)

2) 3)

(Ответ: 1) и 2) и 3) )

3. Составить уравнение плоскости, которая проходит через точку М₁(3;-2;-7) параллельно плоскости . (Ответ: )

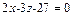
4. Составить уравнение плоскости, которая проходит через две точки М₁(1;-1;-2) и М₂(3;1;1) перпендикулярно к плоскости . (Ответ: )

5. Определить, при каких значениях a и b плоскости 2x-y+3z-1=0, x+2y-z+b=0, x+ay-6z+10=0: 1) имеет одну общую точку; 2) проходят через одну прямую; 3) пересекаются по трем различным параллельным прямым. (Ответ: 1) )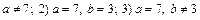

6. Составить уравнение плоскости, которая проходит:

1) через точку М₁(2;-3;3) параллельно плоскости Оху;

7. Вычислить площадь треугольника, который отсекает плоскость 5x-6y+3z+120=0 от координатного угла Оху. (Ответ: 240 кв. ед.)

8. Вычислить объем пирамиды, ограниченной плоскостью 2x-3y+6z-

-12=0 и координатными плоскостями. (Ответ: 8 куб. ед.)

9. Составить уравнение плоскости, которая проходит через точки М₁(-1;4;-1), М₂(-13;2;-10) и отсекает на осях абсцисс и аппликат отличные от нуля отрезки одинаковой длины.

(Ответ: 2x-21y+2z+88=0; 2x-3y-2z+12=0)

10. Вычислить расстояние между параллельными плоскостями:

1) x-2y-2z-12=0, x-2y-2z-6=0; 2) 2x-3y+6z-14=0, 4x-6y+12z+21=0;

3)16x+12y-15z+50=0, 16x+12y-15z+25=0; 4) 2x-y+2z+9=0, 4x-2y+4z-21=0. (Ответ: 1) 2; 2) 3,5; 3) 1; 4) 6,5)

11. На оси Oz найти точку, равноудаленную от точки М(1;-2;0) и от плоскости 3x-2y+6z-9=0. (Ответ: )

12. Составить уравнения плоскостей, параллельных плоскости 2x-2y-z-3=0 и отстоящих от нее на расстояние d=5. (Ответ: 2x-2y-z-18=0; 2x-2y-z+12=0)

13. Составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: 1) 4x-y-2z-3=0, 4x-y-

14. Составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями: 1) x-3y+2z-5=0, 3x-2y-z+3=0; 2) 5x-5y-2z-3=0, x+7y-2z+1=0).

(Ответ: 1) 4x-5y-z-2=0, 2x+y-3z+8=0; 2) x-3y-1=0, 3x+y-2z-1=0)

15. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2x-y+2z-3=0, 3x+2y-6z-1=0, в котором лежит точка М(1;2;-3). (Ответ: 23x-y-4z-24=0)

Прямая в пространстве.

Прямая в пространстве задается несколькими способами.

1. Прямая как линия пересечения двух плоскостей:

(1)

(2)

называется уравнением пучка плоскостей.

2. Канонические уравнения прямой:

, (3)

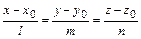
где точка М₀(x₀;y₀;z₀) — точка прямой; — направляющий вектор прямой.

(4)

4. Параметрические уравнения прямой:

(5)

где t — произвольно изменяющийся параметр.

Угол между двумя прямыми

и

равен углу между их направляющими векторами и , т.е. имеет место формула:

(6)

Условие, при котором прямые L₁ и L₂ лежат в одной плоскости:

(7)

Следовательно, прямые скрещиваются, если равенство (7) не имеет место.

Рассмотрим задачи.

Задача. Составить уравнение плоскости , проектирующей прямую на плоскость

Решение. Искомая плоскость проходит через линию пересечения L перпендикулярно к плоскости . Составим уравнение пучка плоскостей:

Обозначим через 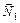и нормали плоскостей и соответственно. Тогда:

Найдем числа 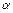и , учитывая, что т.е.

Пусть тогда Подставив эти значения в уравнение пучка, получим:

Задача. Составить канонические и параметрические уравнения прямой

Решение. Чтобы перейти к каноническому и параметрическому заданиям прямой L зафиксируем на ней произвольную точку М₀ и найдем ее направляющий вектор в виде: .

Т.е.

Искомые уравнения: или

Задача. Составить уравнения прямой L₁, которая проходит через точку М₁(-1;2;-3) перпендикулярно к вектору и пересекает прямую .

Решение. Канонические уравнения искомой прямой . Найдем ее направляющий вектор ; для этого решим систему, первое уравнение которой вытекает из перпендикулярности векторов и , а второе — из равенства (7):

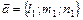
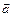
Пусть Тогда

Таким образом,

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные плоскости, признак и условия параллельности плоскостей

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Параллельные плоскости: основные сведения

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .

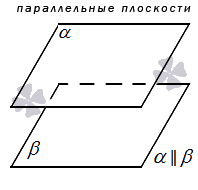
На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Параллельность плоскостей: признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10 — 11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).

Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Заданы две плоскости: 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.

Решение

Запишем систему уравнений из заданных условий:

2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 — 4 равен двум, поскольку минор 2 1 2 3 — 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( — 3 , 1 , 1 ) , C ( — 2 , 2 , — 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.

Решение

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .

Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.

Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( — 3 , 0 , 1 ) и ( — 2 , 2 , — 2 ) . Тогда:

n 1 → = A B → × A C → = i → j → k → — 3 0 1 — 2 1 — 2 = — i → — 8 j → — 3 k → ⇔ n 1 → = ( — 1 , — 8 , — 3 )

Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z — 1 = 0

Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .

Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( — 1 , — 8 , — 3 ) и n 2 → = 1 12 , 2 3 , 1 4

Так как — 1 = t · 1 12 — 8 = t · 2 3 — 3 = t · 1 4 ⇔ t = — 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = — 12 · n 2 → , т.е. являются коллинеарными.

Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.

Видео:Математика это не ИсламСкачать

При каких значениях и уравнения и будут определять параллельные плоскости

№ 1

Найти угол между плоскостями

2x — 4y + 4z — 5 = 0 и -3x +2y + 4z — 5 = 0 .

Решение

Угол между плоскостями определяется углом между соответствующими векторами нормалей к этим плоскостям. Координаты вектора нормали плоскости легко можно определить из общего уравнения плоскости, — это коэффициенты при переменных.

№ 2

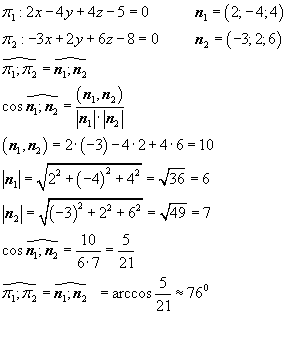
Определить, при каких значениях l и m пара уравненеий

2 x + l y + 3 z — 5 = 0

m x — 6 y — 6 z + 2 = 0

будет определять параллельные плоскости.

Решение

Плоскости параллельны тогда и только тогда, когда векторы нормалей плоскостей коллинеарны:

№ 3

Определить, при каком значении l пара уравненеий

3 x — 5 y + l z — 3 = 0

x + 3 y + 2 z + 5 = 0

будет определять перпендикулярные плоскости.

Решение

Плоскости перпендикулярны тогда и только тогда, когда векторы нормалей плоскостей перпендикулярны, следовательно, их скалярное произведение равно нулю:

Видео:22. Взаимное расположение прямой и плоскости в пространствеСкачать

Определить при каких значениях l и m следущии пары уравнений будут определять параллельные плоскости 3x — y + lz — 9 = 0 ; 2x + my + 2z — 3 = 0?

Алгебра | 10 — 11 классы

Определить при каких значениях l и m следущии пары уравнений будут определять параллельные плоскости 3x — y + lz — 9 = 0 ; 2x + my + 2z — 3 = 0.

3 / 2 = — 1 / m = l / 2 т.

К. условие параллельности плоскосте A1 / A2 = B1 / B2 = C1 / C2

тут это коэфициенты при x, y и z.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Составить уравнение плоскости, которая проходит через точку М (3, 4, — 3) параллельно плоскости x + y + 7z = 0?

Составить уравнение плоскости, которая проходит через точку М (3, 4, — 3) параллельно плоскости x + y + 7z = 0.

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

При каком значении pрешением уравнения — px + 2y + p = 0является пара чисел ( — 1 ; 2)?

При каком значении pрешением уравнения — px + 2y + p = 0является пара чисел ( — 1 ; 2)?

Видео:найти при каких значениях параметра А уравнение будет иметь только 1 корень.Скачать

При каком значении а пара чисел( — 1 ; — 3) является решением уравнения ах — 3у = — 7?

При каком значении а пара чисел( — 1 ; — 3) является решением уравнения ах — 3у = — 7?

Видео:7. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРМЕТРА КОРНЕМ УРАВНЕНИЯ ЯВЛЯЕТСЯ ЛЮБОЕ ЧИСЛОСкачать

Даны две параллельные плоскости альфа и бета?

Даны две параллельные плоскости альфа и бета.

Прямая л лежит в плоскости альфа, опредилите может ли а) прямая л пересекать плоскость бета, б) лежать в плоскости бета, в) быть параллельным.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Если одна прямая параллельна плоскости а другая прямая параллельна этой же плоскости, необходимо ли, чтобы они были параллельны между собой?

Если одна прямая параллельна плоскости а другая прямая параллельна этой же плоскости, необходимо ли, чтобы они были параллельны между собой?

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Вычислите при каком значении а решением уравнения — ах + 4у — а = 0, является пара ( — 2, 3)?

Вычислите при каком значении а решением уравнения — ах + 4у — а = 0, является пара ( — 2, 3).

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

При каком значении коэффициента А плоскость Аx + 3y — 5z + 1 = 0 будет параллельна прямой (х — 1) / 4 = (у + 2) / 3 = z / 1?

При каком значении коэффициента А плоскость Аx + 3y — 5z + 1 = 0 будет параллельна прямой (х — 1) / 4 = (у + 2) / 3 = z / 1.

Видео:15. Взаимное расположение прямых в пространствеСкачать

В каких случаях графики будут параллельны?

В каких случаях графики будут параллельны?

Видео:16. Показать что прямые пересекаются и найти точку их пересечения в пространствеСкачать

Помогите , пожалуйста : Напишите уравнение плоскости, если она проходит через точку B(3, — 2, 2) и : а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox?

Помогите , пожалуйста : Напишите уравнение плоскости, если она проходит через точку B(3, — 2, 2) и : а) параллельна плоскости Oyz ; б) перпендикулярна оси Ox.

Видео:№16 Задачи с параметром. ЕГЭ. Задание 18. При каких значениях параметра А система уравнений...Скачать

1. ) График уравнения у + 12 = 0 на координатной плоскости расположен а) параллельно оси у и проходит через точку х = 12 б) параллельно оси у и проходит через точку х = — 12 в) параллельно оси х и про?

1. ) График уравнения у + 12 = 0 на координатной плоскости расположен а) параллельно оси у и проходит через точку х = 12 б) параллельно оси у и проходит через точку х = — 12 в) параллельно оси х и проходит через точку у = 12 г) параллельно оси х и проходит через точку у = — 12 2.

) Известно, что пара чисел (2 ; — 6) является решением уравнения 7х + ву — 2 = 0.

Если вам необходимо получить ответ на вопрос Определить при каких значениях l и m следущии пары уравнений будут определять параллельные плоскости 3x — y + lz — 9 = 0 ; 2x + my + 2z — 3 = 0?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

💡 Видео

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

5. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ ИМЕЕТ КОРЕНЬ, РАВНЫЙ ЧИСЛУ ... ?Скачать

#67. Сумма квадратов корней в уравнении с параметром!Скачать