Алгебра | 5 — 9 классы
При каких значениях с уравнение 3х ^ 2 — 4х + с = 0 имеет единственный корень?
Единственный корень если дискриминант равен нулю, см.
Вложениеесли можно отметьте как лучший.
- При каких значениях m уравнение имеет единственный корень?
- При каких значениях m уравнение 4x² + 2x — m = 0 имеет один единственный корень?
- При каком значении параметра а уравнение а * х = 3а + х имеет единственный корень?
- При каком значении а уравнение ах = 2а — 3х имеет единственный корень?
- При каких значениях с уравнения x ^ 2 — 8x + c = 0 имеет единственный корень?
- При каких значениях t уравнение имеет единственный корень : tx² — 6x + 1 = 0?
- При каких значения С уравнение имеет x2 — 8x + C = 0 имеет единственный корень?
- При каком значении a имеет единственный корень?
- При каком значении а уравнения 2х ^ 2 + 4х + а = 0 имеет единственный корень?
- Найдите при каком значении «а» уравнение имеет единственный корень?
- При каких значениях c уравнение 3x 2 4x c 0 имеет единственный корень
- Как написать хороший ответ?
- Решение показательных уравнений с параметрами
- 🔍 Видео
Видео:365 Алгебра 9 класс. При каких значениях хСкачать

При каких значениях m уравнение имеет единственный корень?
При каких значениях m уравнение имеет единственный корень?
Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

При каких значениях m уравнение 4x² + 2x — m = 0 имеет один единственный корень?
При каких значениях m уравнение 4x² + 2x — m = 0 имеет один единственный корень?
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

При каком значении параметра а уравнение а * х = 3а + х имеет единственный корень?
При каком значении параметра а уравнение а * х = 3а + х имеет единственный корень?
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

При каком значении а уравнение ах = 2а — 3х имеет единственный корень?
При каком значении а уравнение ах = 2а — 3х имеет единственный корень?
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

При каких значениях с уравнения x ^ 2 — 8x + c = 0 имеет единственный корень?
При каких значениях с уравнения x ^ 2 — 8x + c = 0 имеет единственный корень?
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

При каких значениях t уравнение имеет единственный корень : tx² — 6x + 1 = 0?
При каких значениях t уравнение имеет единственный корень : tx² — 6x + 1 = 0?
Видео:Уравнения с параметром. Алгебра, 8 классСкачать

При каких значения С уравнение имеет x2 — 8x + C = 0 имеет единственный корень?
При каких значения С уравнение имеет x2 — 8x + C = 0 имеет единственный корень.
Видео:Математика При каких значениях параметра а уравнение а٠х^2 + (а^2 + 1)٠х + а = 0 а) имеетСкачать

При каком значении a имеет единственный корень?
При каком значении a имеет единственный корень.
Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

При каком значении а уравнения 2х ^ 2 + 4х + а = 0 имеет единственный корень?
При каком значении а уравнения 2х ^ 2 + 4х + а = 0 имеет единственный корень?
Видео:9кл. При каких значения переменной имеет смысл выражениеСкачать

Найдите при каком значении «а» уравнение имеет единственный корень?
Найдите при каком значении «а» уравнение имеет единственный корень.
Найдите этот корень.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос При каких значениях с уравнение 3х ^ 2 — 4х + с = 0 имеет единственный корень?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
Видео:При каких значениях x ... | ОГЭ 2017 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРАСкачать

При каких значениях c уравнение 3x 2 4x c 0 имеет единственный корень
Вопрос по алгебре:
(1)При каких значениях «с» уравнение 3х^-4x+c=0 имеет единственный корень?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Мы рассматриваем квадратное уравнение. Как известно, один корень квадратное уравнение имеет лишь в том случае, когда дискриминант равен нулю.
Дискриминант находится по формуле D=b^2-4ac, следовательно b^2-4ac должно равняться нулю.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Решение показательных уравнений с параметрами
Разделы: Математика
Цели урока: Учащиеся должны знать способы решений уравнений вида 
Ход урока.
Для первой группы учащихся выдавались следующие задания.
Для каждого значения a решить уравнения:
Задания для второй группы учащихся.
Указать число решений в зависимости от параметра а.
Третья группа решает уравнения, сводящиеся к квадратным.
Задание 1. Решить уравнение p · 4 x – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.
Задание 2. При каких a уравнение 9 x + (2a + 4) · 3 x + 8a + 1 = 0 имеет единственное решение.
Задание 3. Указать число решений уравнения 49 x + 2p · 7 x + p 2 – 1 = 0 в зависимости от параметра p.
Задание 4. При каких значениях p уравнение 4 x – (5p – 3) · 2 x + 4p 2 – 3p = 0 имеет единственное решение.
Выступление первой группы – решение показательных уравнений вида
Докладывает лидер первой группы и привлекает к своему докладу участников этой группы. То есть диалог идёт ученик – ученик.
Решение исходного уравнения сводится к решению линейного уравнения с параметрами kx = b.
Если k = 0, b = 0, то 0 · x = 0, – любое действительное число.
Если k = 0, b ≠ 0, то 0 · x = b – нет решений.
Если k ≠ 0, то 
Задание 1. Решить уравнение 
Докладчик решает у доски с комментариями, остальные записывают в тетрадях.
Значит уравнение (1) можно представить в виде (a – 1)(a + 4)x = (a – 1)(a – 1)(a – 3).
Исследуем полученное уравнение:
Ответ:
На этом выступление первой группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 1.
Выступление второй группы – решение уравнений вида
Докладывает лидер второй группы и привлекает к обсуждению этого вопроса всех учащихся. Исходное уравнение равносильно уравнению ax 2 + bx + c1 = c0, или ax 2 + bx + c = 0.
Далее идёт диалог ученик–ученик.
- Какое уравнение получили? – Это уравнение степени не выше второй.
- При a = 0, bx + c = 0, получили линейное уравнение, которое может иметь одно решение, не иметь корней, или иметь бесконечное множество решений.
- При a ≠ 0, ax 2 + bx + c = 0, квадратное уравнение.
- От чего зависит число решений квадратного уравнения? – Число решений квадратного уравнения зависит от дискриминанта. Если D = 0 то квадратное уравнение имеет одно решение. Если D > 0, то два решения. Если D 2 + 2(a + 3)x + a + 2 = 0.
Ответ:
На этом выступление второй группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 2.
Выступление третьей группы – решение уравнений вида af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Слово предоставляется выступающему от третьей группы. Он докладывает, что их группа решала уравнения вида: (1) af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Исходное уравнение (1) равносильно
Далее докладчик задаёт вопросы, а учащиеся отвечают на них.
При каких условиях уравнение (1) имеет один корень?
- При a = 0 уравнение (2) становится линейным, значит может иметь только один корень, и он должен быть положительным.
- Если D = 0, уравнение (2) имеет один корень, и он должен быть положительным.
- Если D > 0, уравнение (2) имеет два корня, но они должны быть различных знаков.
- Если D > 0, уравнение (2) имеет два корня, но один из низ нуль. А второй положительный.
При каких условиях уравнение (1) имеет два корня?
Исходное уравнение имеет два корня, если уравнение (2) имеет два корня и оба они положительны.
При каких условиях уравнение (1) не имеет корней?
- Если Dx – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.
Ответим на вопрос: При каких значениях p уравнение (1) имеет один корень?
- Если
одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.
Уравнение будет иметь единственное решение при условии. Что дискриминант уравнения (2) есть число положительное, но корни при этом имеют различные знаки. Эти условия достигаются с помощью теоремы Виета. Чтобы корни квадратного трёхчлена были действительными и имели различные знаки, необходимо и достаточно выполнение соотношений.
Итак, уравнение (1) имеет единственное решение при p ≤ 0, p = 4.
Теперь остаётся ответить на вопрос. При каких условиях исходное уравнение (2) имеет два решения? Это возможно, если уравнение (2) имеет два корня и оба они положительны. По теореме Виета для того, чтобы корни квадратного трёхчлена были действительными и при этом оба были положительными, необходимо и достаточно выполнение соотношений.
Исходное уравнение имеет два корня при 0 0, то уравнение (2) имеет корни, но они оба отрицательны.
Итак, D 4. При p > 4 – нет решений. Второе условие равносильно следующим соотношениям.
Значит уравнение (1) не имеет решений при p > 4.
Ответ:
- При p = 4, p ≤ 0 одно решение.
- При 0 4 нет решений.
На этом выступление третьей группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 3.
Домашнее задание.
Задание 1. Найти все значения параметра a, при которых уравнение (a – 3) · 4 x – 8 · 6 x + (a +3) 9 x = 0 не имеет корней.
Задание 2.Указать число решений уравнения p · 2 x + 2 –x – 5 = 0 в зависимости от параметра p.
Задание 3. Выяснить при каких значениях a уравнение 
Задание 4. Найти все значения p при которых уравнение (p – 1) · 4 x – 4 · 2 x + (p + 2) = 0 имеет хотя бы одно решение.
Задание 5. Указать число решений уравнения a · 12 |x| = 2 – 12 –|x| в зависимости от параметра a.
🔍 Видео
Проверь себя, задание 3 - Алгебра 9 класс МерзлякСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

при каких значениях параметра уравнение имеет ровно 3 корняСкачать

Как решить такое уравнение ➜ c³+c²=2 ➜ Решаем на разных множествахСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

Никто не решил ➜ Удобная подстановка ➜ Решите уравнение ➜ x^3-3x+1=0Скачать


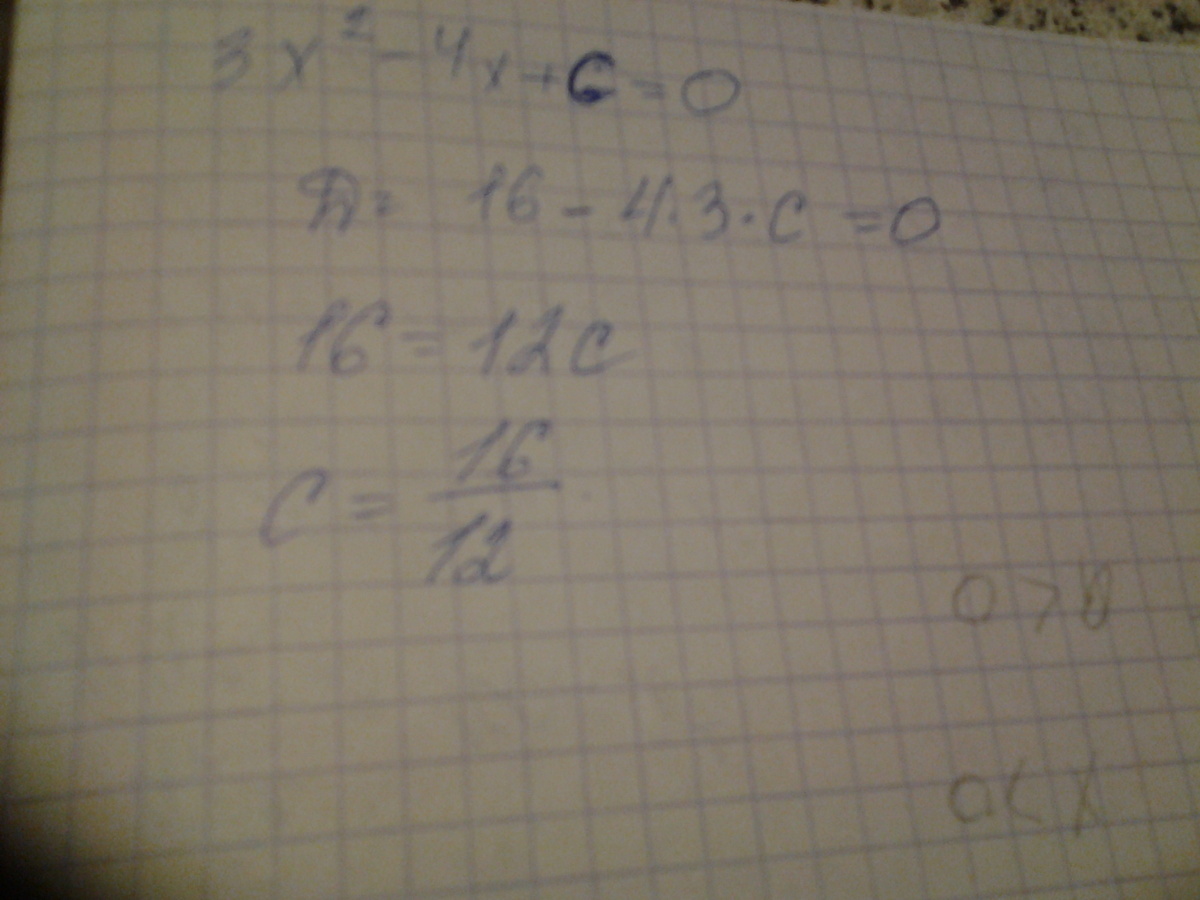
















 одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.
одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.

