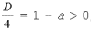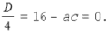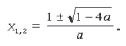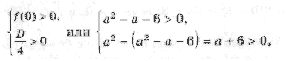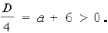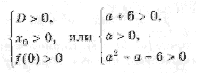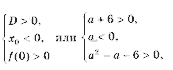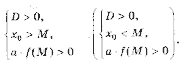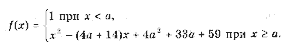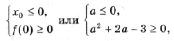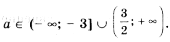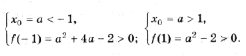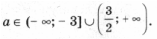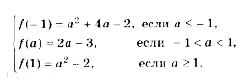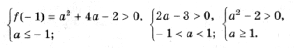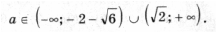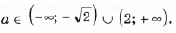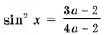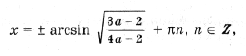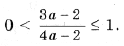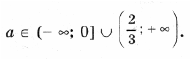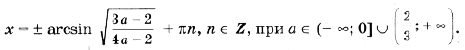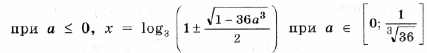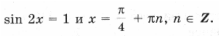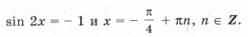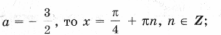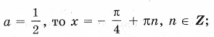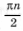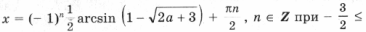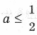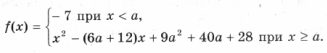Задачи с параметрами относятся к наиболее трудным заданиям, предлагаемым на вступительных экзаменах. Это связано с тем, что они требуют хорошего понимания «глубинных» свойств функций, и их решение носит творческий характер. Однако знание некоторых простых правил и алгоритмов решения необходимо.
Вводные замечания и простейшие примеры
Пример 1. При каких значениях a уравнение ax 2 + 2x + 1 = 0 имеет два различных корня?
Решение.
Данное уравнение является квадратным относительно переменной x при a № 0 и имеет различные корни, когда его дискриминант
т. е. при a
Кроме того, при a = 0 получается уравнение 2x + 1 = 0, имеющее один корень.
Таким образом, a О (– Ґ ; 0) И (0; 1).
Правило 1. Если коэффициент при x 2 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.
Пример 2. Уравнение ax 2 + 8x + c = 0 имеет единственный корень, равный 1. Чему равны a и c?
Решение. Начнем решение задачи с особого случая a = 0, уравнение имеет вид 8x + c = 0. Это линейное уравнение имеет решение x0 = 1 при c = – 8.
При a № 0 квадратное уравнение имеет единственный корень, если
Кроме того, подставив корень x0 = 1 в уравнение, получим a + 8 + c = 0.
Решая систему двух линейных уравнений, найдем a = c = – 4.
Теорема 1.
Для приведенного квадратного трехчлена y = x 2 + px + q (при условии p 2 і 4q)
сумма корней x1 + x2 = – p, произведение корней x1x2 = q, разность корней равна 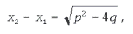
а сумма квадратов корней x1 2 + x2 2 = p 2 – 2q.
Теорема 2.
Для квадратного трехчлена y = ax 2 + bx + c с двумя корнями x1 и x2 имеет место
разложение ax 2 + bx + c = a(x – x1)(x – x2), для трехчлена с одним корнем x0 – разложение
ax 2 + bx + c = a(x – x0) 2 .
Замечание. Часто про квадратные уравнения с дискриминантом, равным нулю и имеющим, соответственно, один корень, говорят, что оно имеет два совпадающих корня (?). Это связано с разложением многочлена на множители, приведенным в теореме 2. (Правильно говорить и понимать в этом случае нужно «один корень кратности два». – Прим. ред.)
Будем обращать внимание на эту тонкость и выделять случай единственного корня кратности 2.
Пример 3. В уравнении x 2 + ax + 12 = 0 определить a таким образом, чтобы разность корней уравнения равнялась единице.
Решение. Разность корней 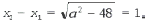
откуда a = ± 7.
Пример 4. При каких a сумма квадратов корней уравнения 2x 2 + 4x + a = 0 равна 6?
Решение. Запишем уравнение в виде 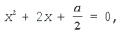
откуда x1 2 + x2 2 = 4 – a = 6 и a = – 2.
Пример 5. При всех a решить уравнение ax 2 – 2x + 4 = 0.
Решение. Если a = 0, то x = 2. Если a № 0, то уравнение становится квадратным. Его дискриминант
равен D = 4 – 16a. Если D 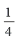
уравнение решений не имеет. Если D = 0, т. е. a = 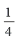
x = 4. Если D > 0, т. е. a
Расположение корней квадратного трехчлена
Графиком квадратного уравнения является парабола, а решениями квадратного уравнения – абсциссы точек пересечения этой параболы с осью Ox. Основой решения всех задач этого параграфа является изучение особенностей расположения парабол с заданными свойствами на координатной плоскости.
Пример 6. При каких a корни уравнения x 2 – 2ax + a 2 – a – 6 = 0 имеют разные знаки?
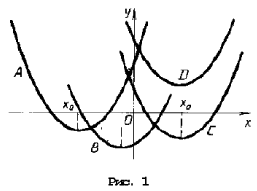
Решение (рис. 1).
Квадратное уравнение либо не имеет решений (график – парабола вида D), либо имеет один или два положительных корня (парабола C), либо имеет один иди два отрицательных корня (парабола A), либо имеет корни разных знаков (парабола B).
Легко сообразить, что последний тип парабол, в отличие от прочих, характеризуется тем, что f(0) 2 – a – 6
Данное решение допускает обобщение, которое мы сформулируем как следующее правило.
Правило 2. Для того чтобы уравнение ax 2 + bx + c = 0
имело два разных корня x1 и x2 таких, что x1
Пример 7. При каких a уравнение x 2 – 2ax + a 2 – a – 6 = 0 имеет два разных корня одного знака?
Решение. Нас интересуют параболы типа A и C (см. рис. 1). Они характеризуются тем, что
откуда a О (– 6; – 2) И (3; + Ґ ).
Пример 8. При каких a уравнение x 2 – 2ax + a 2 – a – 6 = 0 имеет два разных положительных корня?
Решение. Нас интересуют параболы типа C на рис. 1.
Чтобы уравнение имело корни, потребуем
Так как оба корня уравнения по условию должны быть положительными, то и абсцисса вершины параболы, лежащая между корнями, положительна: x0 = a > 0.
Ордината вершины f(x0) 0, то в силу непрерывности исследуемой функции найдется точка x1 О (0; x0) такая, что f(x1) = 0. Очевидно, что это меньший корень уравнения.
Итак, f(0) = a 2 – a – 6 > 0, и, собирая все условия вместе, получим систему
с решением a О (3; + Ґ ).
Пример 9. При каких a уравнение x 2 – 2ax + a 2 – a – 6 имеет два разных отрицательных корня?
Решение. Изучив параболы типа A на рис. 1, получим систему
откуда a О (– 6; – 2).
Обобщим решение предыдущих задач в виде следующего правила.
Правило 3. Для того чтобы уравнение ax 2 + bx + c = 0 имело два разных корня x1 и x2, каждый из которых больше (меньше) M, необходимо и достаточно, чтобы
Пример 10. Функция f(x) задается формулой
Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение.
Решение. Все возможные решения данного уравнения получаются как решения квадратного уравнения
x 2 – (4a + 14)x + 4a 2 + 33a + 59 = 0
с дополнительным условием, что хотя бы один (очевидно, больший) корень x2 і a.
Естественно, чтобы уравнение имело корни, должно быть 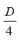
откуда a Ј – 2.
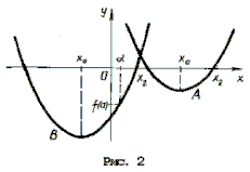
Графиком левой части выделенного уравнения является парабола, абсцисса вершины которой равна x0 = 2a + 7. Решение задачи дают два типа парабол (рис. 2).
A: x0 і a, откуда a і – 7. В этом случае больший корень многочлена x2 і x0 і a.
B: x0 Ј 0, откуда 
В этом случае также больший корень многочлена x2 і a.
Окончательно 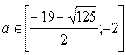
Три решения одного неравенства
Пример 11. Найти все значения параметра a, при которых неравенство x 2 – 2ax + a 2 + 2a – 3 > 0
выполняется:
1) при всех значениях x;
2) при всех положительных значениях x;
3) при всех значениях x О [– 1; 1].
Решение.
Первый способ.
1) Очевидно данное неравенство выполняется при всех x, когда дискриминант отрицателен, т. е.
= a 2 – (a 2 + 2a – 3) = – 2a + 3
откуда a >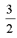
2) Чтобы лучше понять то, что требуется в условии задачи, применим простой прием: на координатной плоскости нарисуем какие-нибудь параболы, а потом возьмем и закроем левую относительно оси Oy полуплоскость. Та часть параболы, которая останется видимой, должна быть выше оси Ox.
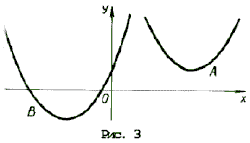
Условие задачи выполняется в двух случаях (см. рис. 3):
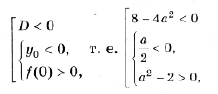
A: график функции y = x 2 – 2ax + a 2 + 2a – 3 лежит выше оси Ox, т. е. D 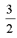
B: оба корня (может быть, один, но двукратный) уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся левее начала координат. По правилу 3 это условие эквивалентно системе неравенств D і 0, x0 Ј 0 и f(0) і 0.
Однако при решении данной системы первое неравенство можно опустить, так как если даже какое-то значение a не удовлетворяет условию D і 0, то оно автоматически попадает в решение пункта A. Таким образом, решаем систему
откуда a Ј – 3.
Объединяя решения пунктов A и B, получим
ответ:
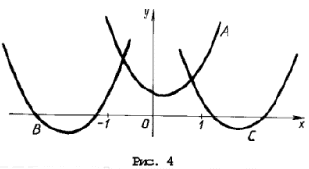
3) Условие задачи выполняется в трех случаях (см. рис. 4):
A: график функции y = x 2 – 2ax + a 2 + 2a – 3 лежит выше оси Ox, т. е. D 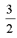
B: оба корня (может быть, один кратности 2) уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся левее – 1. Это условие эквивалентно, как мы знаем из правила 3, системе неравенств D і 0, x0 0;
C: оба корня уравнения x 2 – 2ax + a 2 + 2a – 3 = 0 находятся правее 1.
Это условие эквивалентно D і 0, x0 > 1, f(1) > 0.
Однако в пунктах B и C, также как и в решении предыдущей задачи, неравенство, связанное с дискриминантом, можно опустить.
Соответственно получаем две системы неравенств
Рассмотрев все случаи, получим результат: a >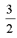
в пункте 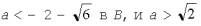
в C.
Ответ задачи – объединение этих трех множеств.
Второй способ. Для того чтобы выполнялось условие каждого из трех пунктов задачи, наименьшее значение функции
y = x 2 – 2ax + a 2 + 2a – 3 на каждом из соответствующих промежутков должно быть положительно.
1) Вершина параболы y = x 2 – 2ax + a 2 + 2a – 3 находится в точке (a; 2a – 3), поэтому наименьшее значение функции на всей числовой прямой равно 2a – 3, и a > 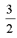
2) на полуоси x і 0 наименьшее значение функции равно f(0) = a 2 + 2a – 3, если a і 0. Разбирая оба случая, получим
3) Наименьшее на отрезке [– 1; 1] значение функции равно
Поскольку наименьшее значение должно быть положительно, получаем системы неравенств
Решение этих трех систем – множество
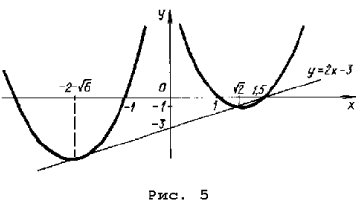
Третий способ. 1) Вершина параболы y = x 2 – 2ax + a 2 + 2a – 3
находится в точке (a; 2a – 3). Нарисуем на координатной плоскости множество, которое образуют вершины всех парабол при различных a (рис. 5).
Это – прямая y = 2x – 3. Напомним, что каждой точке этой прямой соответствует свое значение параметра, и из каждой точки этой прямой «выходит» парабола, соответствующая данному значению параметра. Параболы, целиком находящиеся над осью Ox, характеризуются условием 2a – 3 > 0.
2) Решениями этого пункта являются все решения первого пункта, и, кроме того, параболы, для которых a – отрицательны, и f(0) = a 2 + 2a – 3 і 0.
3) Из рис. 5 видно, что нас интересуют параболы, для которых либо a отрицательно и f(– 1) = a 2 + 4a – 2 > 0,
либо a положительно и f(1) = a 2 – 2 > 0.
Уравнения и неравенства, сводящиеся к квадратным
Пример 12. При каких значениях a уравнение 2x 4 – 2ax 2 + a 2 – 2 = 0 не имеет решений?
Решение. Сделав замену y = x 2 , получим квадратное уравнение f(y) = 2y 2 – 2ay + a 2 – 2 = 0.
Полученное уравнение не имеет решения, когда D
Эти условия могут быть записаны в виде совокупности
откуда
Пример 13. При каждом значении параметра a решить уравнение cos x sin 2x = asin 3x.
Решение. Так как 2cos x sin 2x = sin x + sin 3x и sin 3x = 3sin x – 4sin 3 x,
то уравнение запишется в виде sin x (sin 2 x (4a – 2) – (3a – 2)) = 0.
Отсюда получаем решения x = p n, n О Z при любом a. Уравнение
имеет решения
не совпадающие с решениями первого уравнения, только при условии
Последние ограничения эквивалентны
Ответ: x = p n, n О Z при любом a; кроме того,
Пример 14. Найти все значения параметра a, при каждом из которых неравенство
a 2 + 2a – sin 2 x – 2acos x > 2 выполняется для любого числа x.
Решение. Преобразуем неравенство к виду cos 2 x – 2acos x + a 2 + 2a – 3 > 0
и сделаем замену t = cos x. Важно заметить, что параметр t пробегает значения от – 1 до 1, поэтому задача переформулируется в таком виде: найти все a такие, что
t 2 – 2at + a 2 + 2a – 3 > 0
выполняется при всех t О [– 1; 1]. Эту задачу мы уже решили ранее.
Пример 15. Определить, при каких значениях a уравнение log3 (9 x + 9a 3 ) = x имеет решения, и найти их.
Решение. Преобразуем уравнение к виду 9 x – 3 x + 9a 3 = 0
и, сделав замену y = 3 x , получим y 2 – y + 9a 3 = 0.
В случае, когда дискриминант отрицательный, уравнение решений не имеет. Когда дискриминант
D = 1 – 36a 3 = 0, уравнение имеет единственный корень 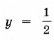
и x = – log3 2. Наконец, когда дискриминант положительный, т. е. 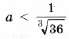
исходное уравнение имеет один корень 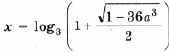
а если, кроме того, выражение 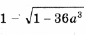
то уравнение имеет еще второй корень 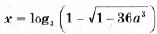
Итак, окончательно получаем 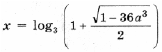
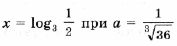
решений нет при остальных a.
Пример 16. Для каждого значения параметра a решить уравнение sin 4 x + cos 4 x + sin 2 x + a = 0.
Решение. Так как 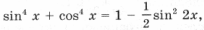
уравнение перепишем в виде sin 2 x – 2sin x – 2a – 2 = 0.
Пусть y = sin 2x, тогда y 2 – 2y – 2a – 2 = 0 (| y | Ј 1).
График функции, стоящей в левой части уравнения, – парабола с вершиной, абсцисса которой y0 = 1; значение функции в точке y = – 1 равно 1 – 2a; дискриминант уравнения равен 8a + 12. Это означает, что больший корень y2 уравнения y 2 – 2y – 2a – 2 = 0, даже если он существует, больше 1, и соответствующее уравнение sin 2x = y2 решений не имеет.
Случай 1. если дискриминант отрицательный, т. е. a
Случай 2. Если дискриминант равен 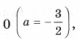
получаем уравнение
Случай 3. Если дискриминант больше 0, т. е. 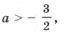
и, кроме того, f(– 1) > 0, то уравнение y 2 – 2y – 2a – 2 = 0 имеет корень 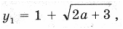
лежащий между – 1 и 1. Соответствующее уравнение 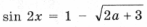
Случай 4. Если f(– 1) = 0, т. е. 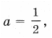
Случай 5. Если дискриминант больше 0, т. е. 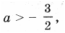
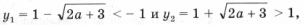
а уравнения 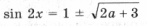
Ответ: если 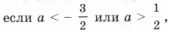
если
если
если 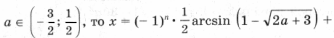
(Случаи 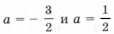
описывает все возможные решения. – Прим. ред.)
Задачи для самостоятельного решения
1. При каких значениях a уравнение ax 2 – 4x + 5 = 0 не имеет корней?
2. При каких значениях a уравнение x 2 – 2ax – 1 = 0 имеет два различных корня?
3. При каких значениях a уравнение 2x 2 + (3a + 1)x + a 2 + a + 2 = 0 имеет хотя бы один корень?
4. Уравнение ax 2 + bx + 5 = 0 имеет единственный корень, равный 1. Чему равны a и b?
5. При каких значениях параметра a корни квадратного уравнения 5x 2 – 7x + a = 0 относятся как 2 к 5?
6. В уравнении ax 2 + 8x + 3 = 0 определить a таким образом, чтобы разность корней уравнения равнялась единице.
7. При каких a сумма квадратов корней уравнения x 2 – 2ax + 2(a + 1) = 0 равна 20?
8. При каких b и c уравнение c + bx – 2x 2 = 0 имеет один положительный и один отрицательный корень?
9. Найти все значения параметра a, при которых один корень уравнения x 2 – (a + 1)x + 2 = 0 больше a, а другой меньше a.
10. Найти все значения параметра a, при которых уравнение x 2 + (a + 1)x + 2 = 0 имеет два разных корня одного знака.
11. При каких значениях a все получающиеся корни уравнения (a – 3)x 2 – 2ax + 6a = 0 положительны?
12. При каких a все получающиеся корни уравнения (1 + a)x 2 – 3ax + 4a = 0 больше 1?
13. Найти все значения параметра a, для которых оба разных корня уравнения x 2 + x + a = 0 будут больше, чем a.
14. При каких значениях a оба корня уравнения 4x 2 – 2x + a = 0 заключены между – 1 и 1?
15. При каких значениях a уравнение x 2 + 2(a – 1)x + a + 5 = 0 имеет хотя бы один положительный корень?
16. Функция f(x) задается формулой
Найдите все значения параметра a, при которых уравнение f(x) = 0 имеет хотя бы одно решение.
17. При каких a неравенство (a 2 – 1)x 2 + 2(a – 1)x + 2 > 0 верно для всех x?
18. При каких значениях параметра a неравенство ax 2 + 2x > 1 – 3a справедливо для всех положительных x?
19. При каких значениях a уравнение x 4 + (1 – 2a)x 2 + a 2 – 1 = 0 не имеет решений?
20. При каких значениях параметра a уравнение 2x 4 – 2ax 2 + a2 – 2 = 0 имеет одно или два решения?
21. При каждом значении a решить уравнение acos x cos 2x = cos 3x.
22. Найти все значения параметра a, при каждом из которых неравенство cos 2 x + 2asin x – 2a 2 – 4 выполняется для любого числа x.
23. При всех a решить уравнение log2 (4 x + a) = x.
24. При каждом значении параметра a решить уравнение sin 2 x + asin 2 2x = sin 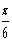
Видео:961 Алгебра 8 класс . При каких значениях уравнение имеет два корня принадлежащие интервалуСкачать

Задача 18 ЕГЭ-2021 по математике. Параметры
Посмотрите на условия задач с параметрами ЕГЭ-2021. Вы заметите, что на вид все они похожи. Однако сходство только внешнее, и решаются они по-разному. В этой статье – обзор задач с параметрами ЕГЭ-2021 по математике.
1. Начнем с задачи, которую лучше всего решить аналитическим способом. Слева в уравнении модуль, справа – произведение модуля и корня квадратного. Лучше всего первым действием сделать возведение обеих частей уравнения в квадрат (при неотрицательности подкоренного выражения).
О том, как решать уравнения, где слева модуль и справа модуль, читайте здесь: Уравнения с модулем.
При каких значениях параметра a уравнение
имеет ровно 2 решения?
Уравнение равносильно системе:
Вынесли общий множитель за скобку
Так как и при всех исходное уравнение имеет корни и при всех Значит, исходное уравнение имеет ровно два корня в следующих случаях:
не имеет решений и
2) совпадение корней
Рассмотрим первый случай.
Неравенство — не имеет решений, если
Рассмотрим второй случай.
1) Корни и совпадают, тогда и
Так как исходное уравнение при имеет один корень
2) Корни и совпадают.
Уравнение имеет корни и
3) Корни и совпадают, исходное уравнение имеет ровно два корня.
Мы применили аналитический способ решения: с помощью равносильных переходов от исходного уравнения перешли к такой форме, где сразу видно, какие корни имеет уравнение при определенных значениях параметра.
На Онлайн-курсе подготовки к ЕГЭ на 100 баллов мы подробно рассказывали об этом методе и решали множество задач. Способ хорош тем, что вы просто действуете по образцу – и быстро приходите к ответу.
2. Второе уравнение очень похоже на первое. И первое действие будет таким же: возведением обеих частей в квадрат. А закончим мы – для разнообразия – построением графиков в системе координат (а; х).
Найти a, при которых имеет ровно 2 решения.
Возведем обе части уравнения в квадрат.
Найдем, каким значениям параметра соответствует ровно два значения
Построим в системе координат графики функций:
Мы находим такие при которых горизонтальная прямая имеет ровно 2 общие точки с совокупностью прямых, являющихся графиком исходного уравнения.
Видим, что в общем случае прямая пересекает каждую из трех прямых, то есть исходное уравнение имеет ровно 3 решения.
Ровно 2 решения будет в случаях, когда прямая проходит через точки пересечения прямых, то есть в случаях совпадения корней.
Данная совокупность имеет ровно два решения в случаях совпадения корней.
О графическом способе решения задач с параметрами читайте здесь: Графический метод решения задач с параметрами.
3. В третьем задании также присутствуют выражения под модулями. Но подход будет другой: мы применим метод интервалов для модулей, о котором можно прочитать здесь: Уравнения с модулем.
С его помощью раскроем модули и получим график функции, заданной описанием: на разных интервалах график этой функции выглядит по-разному, то есть состоит из отдельных кусочков. А дальше – графическое решение.
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Применим метод интервалов для модулей. Уравнение равносильно совокупности систем:
Мы сделали так, потому что при оба модуля раскрываем с противоположным знаком:
Заметим, что если уравнение не выполняется ни при каких
Решим графически полученную совокупность.
Рассмотрим функцию такую, что:
Для функции ось ординат – вертикальная асимптота.
Уравнение имеет ровно два корня при или
Вообще задачи с параметрами, как правило, можно решать многими способами.
4. И наконец, довольно сложное уравнение с тремя модулями. Нам придется раскрывать все эти модули по определению, рассматривая 4 случая. Но ничего страшного здесь нет – просто аккуратность. А потом мы разобьем координатную плоскость (х; а) на области и в каждой из областей построим график уравнения. Кто знаком с методом областей – тот легко с этим справится.
При каких значениях параметра a уравнение имеет ровно три различных решения
Видео:Задача Олимпиады ОММО При каких значениях параметра a уравнение имеет два различных корня суммаСкачать

Задачи с параметром
1. Задача.
При каких значениях параметра a уравнение ( a — 1) x 2 + 2 x + a — 1 = 0 имеет ровно один корень?
1. Решение.
При a = 1 уравнение имеет вид 2 x = 0 и, очевидно, имеет единственный корень x = 0. Если a № 1, то данное уравнение является квадратным и имеет единственный корень при тех значениях параметра, при которых дискриминант квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем уравнение относительно параметра a 4 a 2 — 8 a = 0, откуда a = 0 или a = 2.
1. Ответ: уравнение имеет единственный корень при a О .
2. Задача.
Найти все значения параметра a , при которых имеет два различных корня уравнение x 2 +4 ax +8 a +3 = 0.
2. Решение.
Уравнение x 2 +4 ax +8 a +3 = 0 имеет два различных корня тогда и только тогда, когда D = 16 a 2 -4(8 a +3) > 0. Получаем (после сокращения на общий множитель 4) 4 a 2 -8 a -3 > 0, откуда
| a Ц 7 2 | или a > 1 + | Ц 7 2 |
2. Ответ:
| a О (- Ґ ; 1 – | Ц 7 2 | ) И (1 + | Ц 7 2 | ; Ґ ). |
3. Задача.
Известно, что 
f 2 ( x ) = 6 x — x 2 -6.
а) Постройте график функции f 1 ( x ) при a = 1.
б) При каком значении a графики функций f 1 ( x ) и f 2 ( x ) имеют единственную общую точку?
3. Решение.
3.а. Преобразуем f 1 ( x ) следующим образом


3.б. Сразу отметим, что графики функций y = kx + b и y = ax 2 + bx + c ( a № 0) пересекаются в единственной точке тогда и только тогда, когда квадратное уравнение kx + b = ax 2 + bx + c имеет единственный корень. Используя представление f 1 из 3.а , приравняем дискриминант уравнения a = 6 x — x 2 -6 к нулю. Из уравнения 36-24-4 a = 0 получаем a = 3. Проделав то же самое с уравнением 2 x — a = 6 x — x 2 -6 найдем a = 2. Нетрудно убедиться, что эти значения параметра удовлетворяют условиям задачи. Ответ: a = 2 или a = 3.
4. Задача.
Найти все значения a , при которых множество решений неравенства x 2 -2 ax -3 a і 0 содержит отрезок [3;6].
4. Решение.
Первая координата вершины параболы f ( x ) = x 2 -2 ax -3 a равна x 0 = a . Из свойств квадратичной функции условие f ( x ) і 0 на отрезке [3;6] равносильно совокупности трех систем
| м н о | a Ј 3, f (3) = 9-9 a і 0, | м н о | 3 a D = 4 a 2 +12 a Ј 0, | м н о | a і 6, f (6) = 36-15 a і 0. |
Решением первой системы является множество (- Ґ ,1]. Вторая и третья система решений не имеют.
4. Ответ: a О (- Ґ ,1].
5. Задача (9 кл.)
При каком наименьшем натуральном значении a уравнение
| x 2 +2 ax -3 a +7 = 2 x |
имеет ровно два решения?
5. Решение.
Перепишем это уравнение в виде x 2 + (2 a -2) x — 3 a +7 = 0. Это квадратное уравнение, оно имеет ровно два решения, если его дискриминант строго больше нуля. Вычисляя дискриминант, получаем, что условием наличия ровно двух корней является выполнение неравенства a 2 + a -6 > 0. Решая неравенство, находим a a > 2. Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим натуральным решением второго является число 3.
6. Задача (10 кл.)
Найти все значения a , при которых график функции
| f ( x ) = | x 2 + | ax +2 | a -1 |
6. Решение.
Из условия f (-1) = 1 имеем уравнение
| 1 = | 1+ | — a +2 | a -1 | , |
6. Ответ: a О [2; Ґ ).
7. Задача (10 кл.)
При каких значениях a сумма квадратов корней уравнения
| x 2 -2 ax + a 2 — a = 0 |
7. Решение.
Дискриминант уравнения x 2 -2 ax + a 2 — a = 0 равен 4 a . Поэтому действительные корни этого уравнения существуют, если a і 0. Применяя к данному уравнению теорему Виета получаем x 1 + x 2 = 2 a и x 1 · x 2 = a 2 — a . Отсюда x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 -2 x 1 · x 2 = 2 a 2 +2 a . Решениями неравенства 2 a 2 +2 a > 12, удовлетворяющими условию a і 0, являются числа a > 2.
🌟 Видео
310 Алгебра 9 класс. При каких значениях в Уравнение имеет 2 корня.Скачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

896 Алгебра 8 класс При каких значениях а уравнение Квадратное имеет 2 корня принадлежащиеСкачать

897 Алгебра 8 класс При каких значениях уравнение имеет два отрицательных корня Квадратные уравненияСкачать

5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

РАЗБОР СЛОЖНОГО ЗАДАНИЯ 18, ПАРАМЕТР. ЕГЭ МАТЕМАТИКА с Артуром ШарифовымСкачать

Найдите все значения параметра a, при каждом из которых уравнение имеет ровно два различных корняСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

5. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ ИМЕЕТ КОРЕНЬ, РАВНЫЙ ЧИСЛУ ... ?Скачать

При каких значениях параметра уравнение имеет единственный кореньСкачать

Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать

Параметры 3. Расположение корней квадратного уравнения. ЕГЭ №18Скачать

Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать

Решаем квадратное уравнение с параметромСкачать