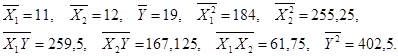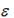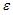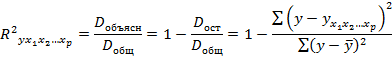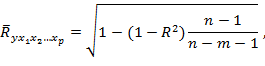МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
2.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Множественная регрессия — уравнение связи с несколькими независимыми переменными
где у— зависимая переменная (результативный признак);

Для построения уравнения множественной регрессии чаще используются следующие функции:
• линейная — 
• степенная –
• экспонента —
• гипербола —
Можно использовать и другие функции, приводимые к линейному виду.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
Для ее решения может быть применён метод определителей:



где 

Другой вид уравнения множественной регрессии — уравнение регрессии в стандартизованном масштабе:

где 


К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:
Связь коэффициентов множественной регрессии 

Параметр a определяется как
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

Для расчета частных коэффициентов эластичности применяется следующая формула:

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:


Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:


Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:


При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:



парных коэффициентов корреляции;

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х1 при неизменном уровне других факторов, можно определить по формуле
или по рекуррентной формуле
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассматривается как квадрат индекса множественной корреляции:

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле
где n — число наблюдений;
m- число факторов.
Значимость уравнения множественной регрессии в целом оценивается с помощью F — критерия Фишера:
Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора xi частный F-критерий определится как
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Съюдента сводится к вычислению значения
где mbi — средняя квадратическая ошибка коэффициента регрессии bi, она может быть определена по формуле:

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности.
Считается, что две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если rxixj≥0,7.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы rxixj (xi≠xj) были бы равны нулю. Так, для включающего три объясняющих переменные уравнения
матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:

так как 
Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:

Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и надежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных Ho: 




Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора xj остатки имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.
При нарушении гомоскедастичности мы имеем неравенства

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта. Основная идея теста Гольдфельда-Квандта состоит в следующем:
1) упорядочение n элементов по мере взрастания переменной x;
2) исключение из рассмотрения С центральных наблюдений; при этом (n—C):2>p, где p-число оцениваемых параметров;
3) разделение совокупности из (n—C) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии;
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию со степенями свободы ((n—C-2p):2) для каждой остаточной суммы квадратов Чем больше величина R превышает табличное значения F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т. д.). Чтобы вест такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т. е. качественные переменные преобразовать в количественные.
Видео:Множественный и частные коэффициенты корреляцииСкачать

Тема: Множественная линейная регрессия
Вопрос: Множественная регрессия— это
*А) регрессия с двумя и более факторными переменными;
Б) с одним фактором;
Вопрос: Факторы эконометрической модели являются коллинеарными, если коэффициент корреляции между ними по модулю больше
Вопрос: Добавление в уравнение множественной регрессии новой объясняющей переменной:
*А) никогда не уменьшает значение коэффициента детерминации;
Б) не оказывает никакого влияние на коэффициент детерминации.
В) увеличивает значение коэффициента детерминации;
Вопрос: Скорректированный коэффициент детерминации:
*А) меньше обычного коэффициента детерминации;
Б) больше обычного коэффициента детерминации;
В) меньше или равен обычному коэффициенту детерминации;
Вопрос: С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
В) не изменяется.
Вопрос: Если коэффициент детерминации, равен нулю то критерий Фишера равен:
В) больше или равен единице.
Вопрос: Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
А) 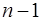
Б) 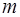
*В) 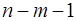
Вопрос: Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
*А) 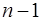
Б) 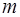
В) 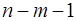
Вопрос: Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
А) 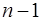
*Б) 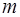
В) 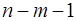
Вопрос: Множественный коэффициент корреляции 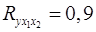

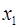
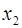
Вопрос: Для построения модели линейной множественной регрессии вида 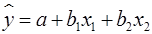
Вопрос: Стандартизованные коэффициенты регрессии 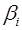
*А) позволяют ранжировать факторы по силе их влияния на результат;
Б) оценивают статистическую значимость факторов;
В) являются коэффициентами эластичности.
Вопрос: Частные коэффициенты корреляции
А) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;
Б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;
*В) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
Вопрос: Частный 
А) оценивает значимость уравнения регрессии в целом;
*Б) служит мерой для оценки включения фактора в модель;
В) ранжирует факторы по силе их влияния на результат.
Вопрос: Состоятельность оценки параметра регрессии, полученной по МНК, означает:
А) что она характеризуется наименьшей дисперсией;
Б) что математическое ожидание остатков равно нулю;
В) увеличение ее точности с увеличением объема выборки.
Вопрос: Укажите истинное утверждение:
А) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;
*Б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;
В) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.
Вопрос: При наличии гетероскедастичности следует применять:
*Б) обобщенный МНК;
В) метод максимального правдоподобия.
Вопрос: Фиктивные переменные – это:
*А) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
Б) экономические переменные, принимающие количественные значения в некотором интервале;
В) значения зависимой переменной за предшествующий период времени.
Вопрос: По 20 наблюдениям построено уравнение регрессии: 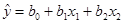
*А) Уравнение значимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
В) Уравнение незначимо при a=0.01.
Вопрос: По 23 наблюдениям построено уравнение регрессии: 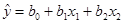
*А) Уравнение значимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
В) Уравнение значимо при a=0.01.
Вопрос: По 24 наблюдениям построено уравнение регрессии: 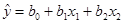
А) Уравнение незначимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
*В) Уравнение незначимо при a=0.01.
Вопрос: По 26 наблюдениям построено уравнение регрессии: 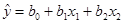
А) Уравнение незначимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
*В) Уравнение значимо при a=0.01.
Вопрос: Построено уравнение множественной регрессии 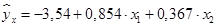
Вопрос: Построено уравнение множественной регрессии 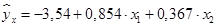
Вопрос: Построено уравнение множественной регрессии 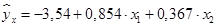
Вопрос: Построено стандартизированное уравнение регрессии 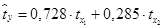
Вопрос: Построено стандартизированное уравнение регрессии 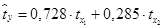
Вопрос: Построено стандартизированное уравнение регрессии 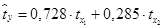
Вопрос: Построено стандартизированное уравнение регрессии 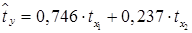
Вопрос: Построено стандартизированное уравнение регрессии 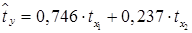
Вопрос: Построено стандартизированное уравнение регрессии 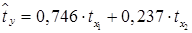
Вопрос: Найдены коэффициенты парной корреляции 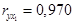
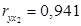
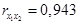
*А) На весьма сильную связь каждого фактора с результатом, а также межфакторную зависимость
Б) Ничего определенного сказать нельзя
В) Связь отсутсвует
Вопрос: В множественном линейном уравнении регрессии строятся доверительные интервалы для коэффициентов регрессии с помощью распределения:
Вопрос: Значение в линейной модели коэффициента детерминации R 2 изменяется:
Вопрос: Множественный коэффициент корреляции равен 0.81. Какой процент дисперсии результативного признака объясняется влиянием всех факторных признаков?
Вопрос: В каких пределах меняется множественный коэффициент корреляции?
А) от — 

Вопрос: При добавлении в уравнение регрессии еще одного объясняющего фактора коэффициент детерминации:
В) сохранит свое значение;
Г) не уменьшится.
Вопрос: Модель в целом статистически значима, если:
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,…,n, где a0 , a1 и a2 – параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a0, полученная методом наименьших квадратов, есть: ………………………………………………………………….
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,…,n, где a0 , a1 и a2 – параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a1, полученная методом наименьших квадратов, есть ………………………………………………………………………..
Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a2, полученная методом наименьших квадратов, есть: ………………………………………………………………………….
Вопрос : . Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Эластичность переменной Y по переменной X1…………………………………………
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Эластичность переменной Y по переменной X2……………………………………………..
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. При увеличении переменной X1 на 1 усл. Ед. переменная Y…………………………………………
*А) увеличится на 0,65 усл.ед.
Б) увеличится на 1 усл.ед.
В) увеличится на 65 усл.ед.
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. При увеличении переменной X2 на 1 усл. Ед. переменная Y………………………………………
*А) уменьшится на 0,14 усл.ед.
Б) увеличится на 0,14 усл.ед
В) уменьшится на 14 усл.ед
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 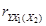
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 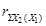
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Коэффициент частной корреляции 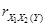
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Множественный коэффициент корреляции 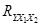
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Скорректированный коэффициент детерминации …………………..
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 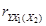
*А) статистически значим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 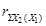
*А) статистически значим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Коэффициент частной корреляции 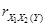
*А) статистически незначим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Остаточная сумма квадратов равна ………………………………………..
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Сумма случайных отклонений равна …………………………………….
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Сумма квадратов отклонений восстановленных значений Y от среднего по выборке равна ……………………………………………………………………………….
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2. n, где a0 , a1 и a2 — параметры, неизвестные статистику и подлежащие оцениванию, а 
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 |
| Y | 0,988 | -0,896 |
| X1 | 0,988 | -0,839 |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Полученное уравнение в целом по F-критерию Фишера ………………..
А) статистически значимо
Б) статистически незначимо
Вопрос: Построено уравнение регрессии 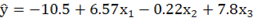
*А) рост переменной x2 на единицу своего измерения приводит к уменьшению среднего значения y на 0,22 единиц своего измерения
Б) рост переменной x2 на 1% приводит к росту среднего значения y на 0,22%
В) рост переменной x2 на единицу своего измерения приводит к росту среднего значения y на 0,22 единиц своего измерения
Вопрос: С увеличением объема выборки:
А) расширяются интервальные оценки
Б) уменьшается ошибка регрессии
*В) увеличивается точность оценок
Г) уменьшается коэффициент детерминации
Вопрос: Число степеней свободы k1 при расчете F-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
*Б) k, где k — количество независимых переменных
Вопрос: Число степеней свободы k2 при расчете F-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
Б) k, где k — количество независимых переменных
Вопрос: Число степеней свободы df при расчете t-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
Б) k, где k — количество независимых переменных
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.5
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.3
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.4
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.25
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.6
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.7
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.7
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.8
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.9
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.65
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:
Вопрос: Величина 
*В) случайной составляющей
Вопрос: В модели вида 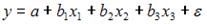
Вопрос: В модели множественной регрессии 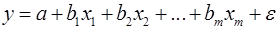
Вопрос: В модели множественной регрессии 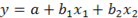
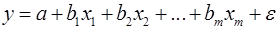
Вопрос: В модели множественной регрессии 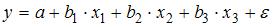
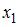
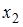
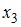
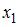
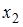
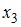
Б) один из них равен нулю
Вопрос: В уравнении линейной множественной регрессии: 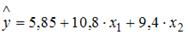
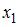
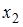
*А) на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
Б) на 1 тыс. руб. … увеличится на 0,108 тыс. руб.
В) на 1 тыс. руб. … увеличится на 10,8 %.
Вопрос: В эконометрической модели линейного уравнения регрессии
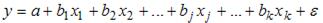
В)
Вопрос: В эконометрической модели линейного уравнения регрессии 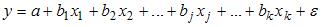
*В)
Вопрос: В модели множественной регрессии 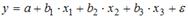
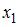
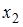
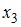
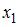
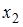
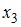
Видео:Математика #1 | Корреляция и регрессияСкачать

Коэффициенты множественной корреляции и детерминации
Общее качество уравнения множественной регрессии оценивается с помощью коэффициента множественной корреляции и его квадрата – коэффициента множественной детерминации.
По аналогии с парной регрессией коэффициент множественной детерминацииможно определить как долю дисперсии результата, объясненную вариацией включенных в модель факторов, в его общей дисперсии:
Значения коэффициента множественной детерминации изменяются от нуля до единицы (0≤R 2 yx1x2…xp≤1). Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение результата.
Коэффициент множественной корреляциихарактеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иными словами, оценивает тесноту связи совместного влияния факторов на результат.
Коэффициент множественной корреляции может быть найден как корень квадратный из коэффициента множественной детерминации:
Значения коэффициентов множественной корреляции изменяются от нуля до единицы (0≤Ryx1x2…xp≤1). Чем ближе коэффициент единице, тем теснее связь между результатом и всеми факторами в совокупности и уравнение регрессии лучше описывает фактические данные. Если множественный коэффициент корреляции Ryx1x2…xp близок к нулю, то уравнение регрессии плохо описывает фактические данные, и факторы оказывают слабое влияние на результат.
Значение коэффициента множественной корреляции больше или равно величине максимального коэффициента парной корреляции:

Если в уравнении регрессии учитывается какой-либо фактор, оказывающий наиболее сильное воздействие на результативный признак, то частный коэффициент корреляции будет достаточно близок к коэффициенту множественной корреляции, но ни в коем случае не больше него.
Иногда для расчета коэффициента множественной корреляции используется еще одна формула (она применима только для линейной множественной регрессии):
где DetІR + І, DetІRІ — определители матриц соответственно парных коэффициентов корреляции и межфакторной корреляции.
Эти определители будут иметь следующий вид для уравнения линейной множественной регрессии с р числом факторов:


т.е. матрица включает все парные коэффициенты корреляции для уравнения регрессии;


т.е. данная матрица получается из предыдущей матрицы путем исключения коэффициентов парной корреляции факторов с результатом (вычеркиваются первая строка и первый столбец).
Для того, чтобы не допустить возможного преувеличения тесноты связи, обычно применяется скорректированный коэффициент множественной корреляции. Он содержит поправку на число степеней свободы. Ocтaточная сумма квадратов отклонений делится на число степеней свободы остаточной вариации (п — т — 1), а общая сумма квадратов отклонений — на число степеней свободы в целом по совокупности (п — 1). Формула скорректированного коэффициента множественной корреляции имеет следующий вид:
где т — число параметров при переменных х (в линейной зависимости оно будет равно числу включаемых в модель факторов = p); п — число наблюдений.
Так как 
а скорректированный коэффициент множественной детерминации
Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.
📸 Видео
Множественный и частные коэффициенты корреляцииСкачать
Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Множественная регрессия в ExcelСкачать

Расчет коэффициента корреляции в ExcelСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Множественная регрессияСкачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Коэффициенты корреляции в ExcelСкачать

Линейная регрессияСкачать

Эконометрика. Линейная парная регрессияСкачать

Коэффициент корреляции. Статистическая значимостьСкачать

РегрессияСкачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

08 06 Корреляция и регрессияСкачать

Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать