Презентация была опубликована 6 лет назад пользователемИнна Шульц
- Похожие презентации
- Презентация 10 класса по предмету «Математика» на тему: «Решение систем линейных уравнений матричными методами Выполнила : Донец Елизавета, ученица 10 В класса. Научный руководитель : Симакова М. Н., учитель.». Скачать бесплатно и без регистрации. — Транскрипт:
- Презентация на тему «Решение систем трех линейных уравнений матричным методом»
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Подарочные сертификаты
- Презентация на тему: Системы линейных алгебраических уравнений (СЛАУ)
- 📹 Видео
Похожие презентации
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Презентация 10 класса по предмету «Математика» на тему: «Решение систем линейных уравнений матричными методами Выполнила : Донец Елизавета, ученица 10 В класса. Научный руководитель : Симакова М. Н., учитель.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Решение систем линейных уравнений матричными методами Выполнила : Донец Елизавета, ученица 10 В класса. Научный руководитель : Симакова М. Н., учитель математики Симаков Е. Е., преподаватель спецкурса по информатике
2 Задачи: Рассмотреть понятие матрицы, области применения, основные действия над матрицами. Изучить способы решения систем линейных уравнений матричными методами. Применить изученные методы на практике для решения систем линейных алгебраических уравнений в программе MathCAD. Цель: Сравнение матричных методов решения с классическими методами, изучаемыми в школьном курсе и реализация решений в программе MathCAD.
3 Матрица – прямоугольная таблица чисел, содержащая n строк одинаковой длины или n столбцов одинаковой длины. A m×n = (а ij ) i= — номер строки,j= — номер столбца Квадратная матрица Единичная матрица Нулевая матрица Треугольная матрица Матрица — вектор
4 Решение систем линейных алгебраических уравнений с помощью матричных вычислений a ij, i = — коэффициенты системы b i – свободные члены А · Х = В Х – вектор-столбец из неизвестных x j, В – вектор-столбец из свободных членов b i.
5 x 1 = с 1, x 2 = с 2 …, x n = с n Решение системы
6 Метод Гаусса k n, a ii 0, i = a ii — главные элементы системы
7 общее решение системы: х 2 = 5 х х 3 – 3; х 1 = 5 х х 3 – 1. Если предположить, например, х 3 = 0, х 4 = 0, то х 1 = -1, х 2 =-3, х 3 = 0, х 4 = 0. Метод Гаусса
Х = А -1 · В матричный способ решения системы. Формула Крамера» title=»А · Х = В | А -1 A -1 · А · Х = В · А -1 А -1 · А = Е и Е · Х = Х => Х = А -1 · В матричный способ решения системы. Формула Крамера» > 8 А · Х = В | А -1 A -1 · А · Х = В · А -1 А -1 · А = Е и Е · Х = Х => Х = А -1 · В матричный способ решения системы. Формула Крамера Х = А -1 · В матричный способ решения системы. Формула Крамера»> Х = А -1 · В матричный способ решения системы. Формула Крамера»> Х = А -1 · В матричный способ решения системы. Формула Крамера» title=»А · Х = В | А -1 A -1 · А · Х = В · А -1 А -1 · А = Е и Е · Х = Х => Х = А -1 · В матричный способ решения системы. Формула Крамера»>
9 A 11 b 1 + A 21 b 2 + … + A n1 b n — разложение определителя Формула Крамера
10 Вывод Плюсы решения в MathCAD: от пользователя не требуется самому проводить преобразования ; программный код является универсальным, требующими только смены условия ; возможность экспортирования результатов в другие программы.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Презентация на тему «Решение систем трех линейных уравнений матричным методом»
Описание презентации по отдельным слайдам:
Решение систем трех линейных уравнений матричным методом. Преподаватель ДППК Трохимюк О.В.
Цели занятия: сформировать: — понятие о матрицах, их видах, действиях над ними; — о матричным методом методе решения системы трех линейных уравнений с тремя переменными; воспитывать стремление к познанию, внимательное отношение к делу, аккуратность, самостоятельность, творческое отношение к учебной деятельности; развивать логическое и аналитическое мышление; прививать интерес к поисковой деятельности.
Математика является универсальным языком, который широко применяется во всех сферах человеческой деятельности. Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц. Актуальность этой темы усиливается в связи с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Матрица, её история и применение Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Термин «матрица» имеет много значений. Матрица — (нем., Matrize, от лат. matrix матка). 1) в литейном производстве: медная форма для отливки букв, а также монет. 2) в типографском деле: бумажная форма для отливки стереотипа. В программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Матрица в фотографии – это интегральная микросхема, которая состоит из фотодиодов (светочувствительных элементов).
План 1. Определение обратной матрицы. 2. Нахождение обратной матрицы. 3. Решение системы трех линейных уравнений с тремя неизвестными методом обратной матрицы.
Ключевые понятия и термины: матрица; определитель матрицы; квадратная матрица; прямоугольная матрица; виды матриц; обратная матрица; алгоритм нахождения обратной матрицы; алгебраические дополнения.
Литература 1. Алгебра и начала математического анализа: учебник для общеобразоват. организаций: базов. и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – М.: Просвещение, 2016. – 463 с. 2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с. 3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001. 4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001. 5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
Вопросы к теме Что такое матрицы и зачем они нужны? Какие виды матриц существуют? Как найти определитель матрицы? Какие операции можно выполнять над матрицами? Какая матрица называется обратной? Как найти обратную матрицу? Как решить систему трех линейных уравнений с тремя переменными методом обратной матрицы?
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка:
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка: 3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка: 3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
4. Проведем короткий анализ домашней работы. 5. Проверить определитель второго порядка из домашнего задания 6. Проверить определитель третьего порядка из домашнего задания
Изложение теоретического материала и его закрепление
1. Матрица – это упорядоченная таблица чисел которая имеет m строк и n столбцов.
Числа это элементы матрицы. Следует помнить, что определитель – это величина, которую изображают в виде квадратной таблицы; матрица – это всегда таблица чисел, никак по-другому не определяема. Если , то матрица прямоугольная, если , то – квадратная. прямоугольная матрица размером квадратная матрица ІІ порядка. диагональная матрица ІІІ порядка.
нулевая матрица размером единичная матрица. матрица — столбец. матрица – строка.
Равенство матриц Две матрицы с одинаковыми размерами равны, если их соответствующие элементы равны: и , то A=B, Так если
Транспонирование матрицы Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной.
Где ещё применяются матрицы? Теперь подробнее остановимся на некоторых областях применения матриц. Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме. С помощью матриц удобно записывать некоторые экономические зависимости.
Ресурсы Отрасли экономики Промышленность Сельское хозяйство Электроэнергия 5,3 4,1 Трудовые ресурсы 2,8 2,1 Водные ресурсы 4,8 5,1
В данной записи, например, матричный элемент показывает, сколько электроэнергии употребляет промышленность, а элемент — сколько трудовых ресурсов потребляет сельское хозяйство. С помощью матриц можно решать системы уравнений, в них удобно представлять какие-либо данные. Таким образом, мы пришли к выводу, что матрицы широко применялись и применяются до сих пор.
Произведением двух матриц АВ является матрица С, элемент которой равен сумме произведений соответствующих элементов i — той строки матрицы А и j — того столбца матрицы В. (Чтобы получить i-тую строку произведения, необходимо умножить i-тую строку матрицы А на каждый столбец матрицы В) Чтобы умножать матрицы, необходимо, чтобы количество столбцов матрицы А было равно количеству строк матрицы В. Размер А: m×n; размер В: n×p, то размер АВ: m×p.
Свойства произведений матриц
Пример 1. Пример 2.
2. Обратная матрица. Матрицей называют обратной к квадратной матрице А, если произведение этих матриц равняется единичной матрицей, то есть Обратная матрица существует для всякой невырожденной квадратной матрицы А, то есть когда определитель матрицы Обратная матрица невырожденной квадратной матрицы А находится по формуле: — определитель матрицы А, — алгебраические дополнения элементов определителя .
— определитель матрицы А, — алгебраические дополнения элементов определителя Запишем алгоритм нахождения обратной матрицы для квадратной матрицы А: 1) вычислить определитель матрицы А. Если , то матрица А имеет обратную, в противном случае обратной матрицы не существует; 2) вычислить алгебраические дополнения элементов матрицы А; 3) Записать обратную матрицу 4) проверить правильность вычислений: Алгебраические дополнения в обратной матрице записываются не по строкам, а по столбцам.
Матрицы можно подвергать элементарным преобразованиям: 1. Можно менять местами строки и столбцы. 2. Можно строку (столбец) умножать на одно и то же число. 3. К некоторой строке или столбцу можно прибавить другую строку (столбец), умноженную на некоторое число. Такие преобразования приводят к замене строк или столбцов строками (столбцами), состоящими из нулей, которые надо удалять из матрицы для рассмотрения матрицы меньшего размера.
Нахождение обратной матрицы Пример1. Определить обратную матрицу для матрицы Решение. Вычислим определитель матрицы А: то для матрицы А существует обратная матрица . Запишем алгебраические дополнения элементов матрицы А:
Нахождение обратной матрицы Пример1. Определить обратную матрицу для матрицы Решение. Вычислим определитель матрицы А: то для матрицы А существует обратная матрица . Запишем алгебраические дополнения элементов матрицы А:
Проверка правильности вычислений: (Сделать вывод. Для матриц А и справедлив переместительный закон умножения). Делаем вывод. Для матриц А и справедлив переместительный закон умножения. Ответ:
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы Решение. Вычислим определитель матрицы А: то для матрицы А существует обратная матрица Запишем алгебраические дополнения элементов матрицы А: Обратная матрица имеет вид:
3. Решение система трех линейных уравнений с тремя неизвестными методом обратной матрицы Пусть задана система трех линейных уравнений с тремя неизвестными Если основная матрица системы линейных уравнений является квадратной и невырожденной, то систему можно решить матричным способом (с помощью обратной матрицы). Записав систему в матричном виде, получим решение X системы уравнений: А- матрица, составленная из коэффициентов при переменных x. y. z . Х- матрица – столбец составленная из переменных величин. В- матрица – столбец составленная из свободных членов.
Пример 1. Решить систему трех линейных уравнений с тремя неизвестными методом обратной матрицы: Решение. Запишем систему в матричном виде , где Решение матричного уравнения будет иметь вид: Найдем обратную матрицу Сначала найдем главный определитель матрицы:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Так как , то умножим обратную матрицу на матрицу столбец :
Так как , то умножим обратную матрицу на матрицу столбец :
Так как , то умножим обратную матрицу на матрицу столбец : Ответ:
Так как , то умножим обратную матрицу на матрицу столбец : Проверка: Ответ:
Подведение итогов занятия. Благодарю за работу на занятии. Подсчитываем поощрительные баллы. Оценки комментируются и выставляются в журнал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 69 регионов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 587 493 материала в базе
Другие материалы
- 15.01.2017
- 526
- 1
- 15.01.2017
- 708
- 0
- 15.01.2017
- 446
- 0
- 15.01.2017
- 2231
- 36
- 15.01.2017
- 374
- 0
- 15.01.2017
- 441
- 0
- 15.01.2017
- 17403
- 498
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.01.2017 2852
- PPTX 1.1 мбайт
- 66 скачиваний
- Рейтинг: 3 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Трохимюк Ольга Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 50298
- Всего материалов: 20
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей
Время чтения: 1 минута
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Только 23 февраля!
Получите новую
специальность
по низкой цене
Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
Видео:Матричный метод решения систем уравненийСкачать

Презентация на тему: Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ)
Здесь — неизвестные; Здесь — неизвестные; — коэффициенты при неизвестных, где — номер уравнения, — номер неизвестного; — свободные члены (правые части).
Система наз. неоднородной, если не все равны нулю. Система наз. неоднородной, если не все равны нулю. Система наз. однородной, если все равны нулю.
Матрица системы Матрица системы
Решением системы будем называть Решением системы будем называть упорядоченный набор чисел обращающий каждое уравнение системы в верное равенство.
Решить систему — значит найти Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система, имеющая хотя бы одно решение, называется совместной. Если система имеет только одно решение, то она называется определенной.
Если система не имеет решений, то Если система не имеет решений, то она называется несовместной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной). Если число уравнений системы совпадает с числом неизвестных , то система называется квадратной.
Две системы, множества решений Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.
Рассмотрим квадратную систему: Рассмотрим квадратную систему:
Исходную систему можно представить в виде таблицы: Исходную систему можно представить в виде таблицы:
Полученная матрица соответствует системе: Полученная матрица соответствует системе:
С помощью этого метода можно решать квадратные системы линейных уравнений С помощью этого метода можно решать квадратные системы линейных уравнений
Систему можно записать в виде Систему можно записать в виде где
Если матрица невырожденная, то Если матрица невырожденная, то можно выполнить преобразования
Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуле Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуле
📹 Видео
Решение системы уравнений методом ГауссаСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение системы уравнений методом Крамера.Скачать

Матричный метод решения систем линейных уравнений (метод обратной матрицы)Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

6 способов в одном видеоСкачать

Решить систему линейных уравнений по формулам Крамера и матричным методом.Скачать

Крамера. Гаусса. Матричный метод. Система линейных уравнений. 3 способа решенияСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение систем линейных уравнений с помощью матрицСкачать

Видеоурок "Матричный метод"Скачать

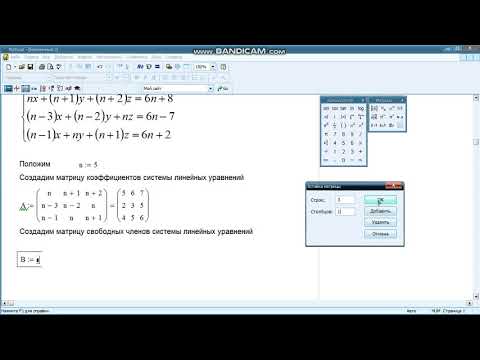
MathCAD Решение системы линейных уравнений матричным методомСкачать