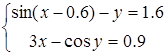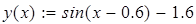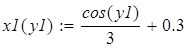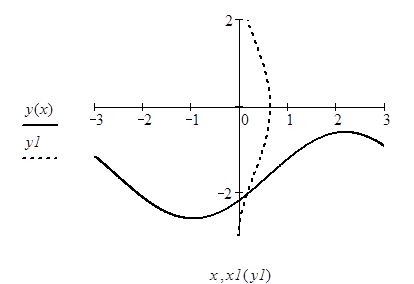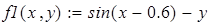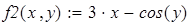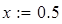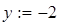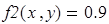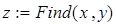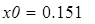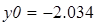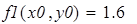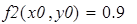Дата добавления: 2015-07-23 ; просмотров: 1622 ; Нарушение авторских прав
MathCAD дает также возможность численно решать также и системы нелинейных уравнений с помощью функции Find(z1, z2, . . .,zn),которая возвращает приближенное решение системы уравнений с числом уравнений равным числу неизвестных..[5] Это число должно быть равно числу аргументов функции Find.
Решение проводится в следующем порядке:
Ø Задать начальное приближение для всех неизвестных, входящих в систему уравнений.
Ø Напечатать ключевое слово Given. Оно указывает MathCAD, что далее следует система уравнений.
Ø Ввести уравнения и неравенства в любом порядке с использованием знаков логических операций между их левыми и правыми частями знаков =, , ³, £ палитры Boolean (Логический) Для печати символа = [6] можно использовать сочетание клавиш Ctrl+”=”
Ø Ввести выражение, которое включает функцию Find, например:
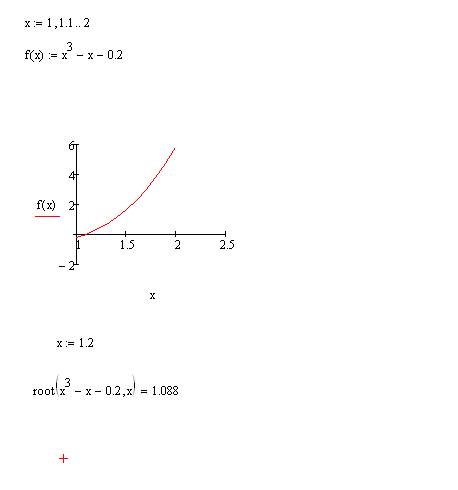
Пример на рис. 20 иллюстрирует решение системы уравнений
Для нахождения начального приближения преобразуем уравнения системы к виду f 1(x) = y и f 2 (y)= x
В документе MathCAD построим графики функций f 1(x) = y и f 2 (y)= x и найдем окрестность точки пересечения.
Рис. 20. Определение начального приближения для решения системы уравнений
В качестве начального приближения можно взять произвольную точку из этой окрестности. Затем записывается вычислительный блок Given — Find, находится решение и делается проверка (рис. 21).
Начальное приближение 
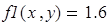
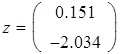
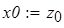
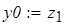
Проверка 
Рис. 21. Решение системы нелинейных уравнений
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое–либо выражение, содержащее функцию Find, называют блоком решения уравнений.
В блоке решения недопустимо использовать следующие выражения:
Ø Ограничения со знаком ¹.
Ø Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
- Системы с нелинейными уравнениями
- Нелинейные уравнения с двумя неизвестными
- Системы из двух уравнений, одно из которых линейное
- Однородные уравнения второй степени с двумя неизвестными
- Системы из двух уравнений, одно из которых однородное
- Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
- Примеры решения систем уравнений других видов
- Лабораторная работа 2. Решение уравнений средствами Mathcad
- 📽️ Видео
Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
Системы с нелинейными уравнениями
 Нелинейные уравнения с двумя неизвестными |
| Системы из двух уравнений, одно из которых линейное |
| Однородные уравнения второй степени с двумя неизвестными |
| Системы из двух уравнений, одно из которых однородное |
| Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное |
| Примеры решения систем уравнений других видов |
Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать
Нелинейные уравнения с двумя неизвестными
Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
| z = f (x , y) , | (1) |
причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .
Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
| f (x , y) = 0 , | (2) |
где f (x , y) – любая функция, отличная от функции
где a , b , c – заданные числа.
Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1 . Решить уравнение
| x 2 – 4xy + 6y 2 – – 12 y +18 = 0 . | (3) |
Решение . Преобразуем левую часть уравнения (3):
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y) 2 + 2(y – 3) 2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
решением которой служит пара чисел (6 ; 3) .
Пример 2 . Решить уравнение
| sin (xy) = 2 . | (5) |
вытекает, что уравнение (5) решений не имеет.
Ответ : Решений нет.
Пример 3 . Решить уравнение
| ln (x – y) = 0 . | (6) |
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
где y – любое число.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Системы из двух уравнений, одно из которых линейное
Определение 4 . Решением системы уравнений
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4 . Решить систему уравнений
 | (7) |
Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
Таким образом, решениями системы (7) являются две пары чисел
и 
Ответ : (– 1 ; 9) , (9 ; – 1)
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать
Однородные уравнения второй степени с двумя неизвестными
Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
где a , b , c – заданные числа.
Пример 5 . Решить уравнение
| 3x 2 – 8xy + 5y 2 = 0 . | (8) |
Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
Ответ . Решениями уравнения (8) являются все пары чисел вида
( y ; y) или 
где y – любое число.
Следствие . Левую часть уравнения (8) можно разложить на множители
Видео:Решение систем уравнений методом подстановкиСкачать
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6 . Решить систему уравнений
 | (9) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .
,
из второго уравнения системы (9) получаем уравнение
которое корней не имеет.
Ответ : (– 2 ; 2) , (2 ; – 2)
Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7 . Решить систему уравнений
 | (10) |
Решение . Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
 | (11) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
которое корней не имеет.
,
из второго уравнения системы (11) получаем уравнение
,
корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ : (– 2 ; 3) , (2 ; – 3)
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Примеры решения систем уравнений других видов
Пример 8 . Решить систему уравнений (МФТИ)
Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
из которой находим
 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что 
, поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9 . Решить систему из двух уравнений с тремя неизвестными
 | (17) |
Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Ответ : (4 ; 4 ; – 4)
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать
Лабораторная работа 2. Решение уравнений средствами Mathcad
Решение уравнений средствами Mathcad
Упражнение 2.
| x 4 + 9x 3 + 31x 2 + 59x+ 60 |
Упражнение 3.Решить систему линейных уравнений (Таблица 3):
1) используя функцию Find;
2) матричным способом и используя функцию lsolve.
Упражнение 4. Преобразовать нелинейные уравнения системы из Таблицы 4 к виду f 1(x) = y и f 2 (y)= x. Построить их графики и определить начальное приближение решения. Решить систему нелинейных уравнений с помощью функции Minerr.
Упражнение 5. Символьно решить системы уравнений:
Не нашли, что искали? Воспользуйтесь поиском:
📽️ Видео
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Нелинейные уравнения. Практическая часть. 9 класс.Скачать
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
СИСТЕМА УРАВНЕНИЙ нелинейных 9 класс алгебраСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Линейное уравнение с двумя переменными. 7 класс.Скачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Решение системы неравенств с двумя переменными. 9 класс.Скачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Нелинейные уравнения. Практическая часть. 9 класс.Скачать
Решение нелинейных уравнений.Скачать
Системы нелинейных уравнений с двумя переменными. Способ подстановки. Алгебра 9 классСкачать
