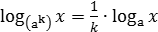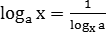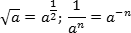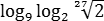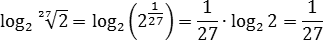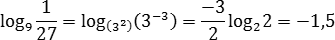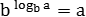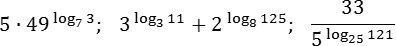Преобразование показательных и логарифмических выражений решение уравнений

В задаче B7 дается некоторое выражение, которое нужно упростить. В результате должно получиться обычное число, которое можно записать в бланке ответов. Все выражения условно делятся на три типа:

1. Логарифмические,
2. Показательные,
3. Комбинированные.

Показательные и логарифмические выражения в чистом виде практически не встречаются. Однако знать, как они вычисляются, совершенно необходимо.

В целом, задача B7 решается достаточно просто и вполне под силу среднему выпускнику. Отсутствие четких алгоритмов компенсируется в ней стандартностью и однообразностью. Научиться решать такие задачи можно просто за счет большого количества тренировок.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Логарифмические выражения

Подавляющее большинство задач B7 содержат логарифмы в том или ином виде. Эта тема традиционно считается сложной, поскольку ее изучение приходится, как правило, на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате многие выпускники имеют весьма смутное представление о логарифмах.

Но в этой задаче никто и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые простые выражения, которые требуют незамысловатых рассуждений и вполне могут быть освоены самостоятельно. Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:

1. log _a x + log _a y = log _a ( x · y )
2. log _a x − log _a y = log _a ( x : y )
3. log _a x n = n · log _a x
4. 
5. 

Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:

Первые два выражения преобразуются как разность логарифмов:
log₆ 270 − log₆ 7,5 = log₆ (270 : 7,5) = log₆ 36 = 2;
log₅ 775 − log₅ 6,2 = log₅ (775 : 6,2) = log₅ 125 = 3.

Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:

Конструкции вида log _a log _b x многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. log _a (log _b x ). Сначала вычисляется внутренний логарифм (положим log _b x = c ), а затем внешний: log _a c .

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Показательные выражения

Будем называть показательным выражением любую конструкцию вида a k , где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.

Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.

1. a n · a m = a n + m ;
2. a n / a m = a n − m ;
3. ( a n ) m = a n · m ;
4. ( a · b ) n = a n · b n ;
5. ( a : b ) n = a n : b n .

Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.

Задача. Найти значения выражений: 7 9 · 3 11 : 21 8 , 24 7 : 3 6 : 16 5 , 30 6 : 6 5 : 25 2 .

Решение. Разложим все основания степеней на простые множители:
7 9 · 3 11 : 21 8 = 7 9 · 3 11 : (7 · 3) 8 = 7 9 · 3 11 : (7 8 · 3 8 ) = 7 9 · 3 11 : 7 8 : 3 8 = 7 · 3 3 = 189.
24 7 : 3 6 : 16 5 = (3 · 2 3 ) 7 : 3 6 : (2 4 ) 5 = 3 7 · 2 21 : 3 6 : 2 20 = 3 · 2 = 6.
30 6 : 6 5 : 25 2 = (5 · 3 · 2) 6 : (3 · 2) 5 : (5 2 ) 2 = 5 6 · 3 6 · 2 6 : 3 5 : 2 5 : 5 4 = 5 2 · 3 · 2 = 150.

Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Комбинированные задачи

Если знать формулы, то все показательные и логарифмические выражения решаются буквально в одну строчку. Однако в задаче B7 степени и логарифмы могут объединяться, образуя довольно неслабые комбинации.

Из определения логарифма вытекают две формулы, которые постоянно встречаются в реальных задачах. Эти формулы позволяют заменить знак логарифма нормальными числами:

1. log _a a n = n
2. 

В чистом виде они, как правило, не встречаются, поэтому общая схема решения комбинированных задач выглядит так:

1. Записать там, где это возможно, числа в виде степеней. Например, 25 = 5 2 , 16 = 2 4 , 27 = 3 3 . дальше сами. Корни и дроби тоже надо заменить степенями по уже известным формулам:
   
2. Избавиться от степеней в основаниях логарифмов, если они там есть. Затем все множители, стоящие перед знаком логарифма, нужно внести в аргумент. Например, 5 · log₇ 2 = log₇ 2 5 = log₇ 32.
3. Воспользоваться формулами замены логарифмов, которые приведены выше. Как правило, этого будет достаточно.

На первый взгляд эта схема кажется громоздкой и далеко не оптимальной. Но стоит немного потренироваться — и комбинированные задачи будут решаться за несколько секунд. Особо продвинутые решают их устно.

Задача. Найти значения выражений:

Будем действовать по схеме. Для первого выражения все очевидно:

Видео:БАЗА. Преобразование и решение показательных и логарифмических уравненийСкачать

Презентация на тему: Практическая работа: «Тождественные преобразования показательных и логарифмических выражений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Практическая работа: «Тождественные преобразования показательных и логарифмических выражений.»

Цель работы: * Закрепить знания , умения и навыки решения простейших показательных и логарифмических уравнений и неравенств. * обобщить и систематизировать изученные методы решения показательных и логарифмических уравнений * Дать определение логарифма * показать почему возникли логарифмы * показать полезность применения логарифмов * развивать интерес к истории математики

Разбить уравнения на группы по методу их решения: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.

Разбить уравнения на группы по методу их решения: По определению 2. 4. Метод замены переменной 10. 5. 3. Метод потенцирования 7. 11. 1. Метод логарифмирования 6. 8. 12.

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=3

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=0,01

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=0,09

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=2

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=31

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=125

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=1

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=2

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=8

Блиц-турнир Ответ: х =

Блиц-турнир Ответ: х = 1,2

Блиц-турнир Ответ: х=

Блиц-турнир Ответ: х=76

Для чего нужны логарифмы? Для чего вообще нужны логарифмы? Какая от них практическая польза? Пожалуй, лучше всего ответил на эти вопросы знаменитый математик, физик и астроном Пьер-Симон Лаплас (1749-1827). По его мнению, изобретение такого показателя, как логарифм, словно удваивает жизнь астрономов, сокращая вычисления нескольких месяцев в труд нескольких дней. Некоторые на это могут ответить: мол, любителей тайн звездного неба сравнительно немного, а остальным-то людям что дают логарифмы? Говоря про астрономов, Лаплас имел в виду, прежде всего, тех, кто занимается сложными вычислениями. А изобретение логарифмов очень облегчило эту работу

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 952 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Преобразование логарифмических выраженийСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 565 316 материалов в базе

Другие материалы

• 02.06.2017
• 286
• 0

• 02.06.2017
• 408
• 0

• 02.06.2017
• 1834
• 1

• 02.06.2017
• 645
• 0

• 02.06.2017
• 372
• 0

• 02.06.2017
• 2522
• 29

• 02.06.2017
• 338
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 02.06.2017 1648
• PPTX 3.4 мбайт
• 67 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Рыгалова Надежда Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 10 месяцев
• Подписчики: 1
• Всего просмотров: 50846
• Всего материалов: 22

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Логарифмические уравнения. 11 класс.Скачать

Преобразование выражений с использованием свойств логарифмов: примеры, решения

Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.

В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.

Видео:Показательные уравнения. 11 класс.Скачать

Свойства логарифмов

Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: a log a b = b , a > 0 , a ≠ 1 , b > 0 . Также нужно помнить следующие свойства:

1. log a 1 = 0 при любом a > 0 , a ≠ 1 .
2. log a a = 1 , если a > 0 , a ≠ 1 .
3. log_aa=1 log a a = 1 при любом a > 0 , a ≠ 1 .
4. log a a = 1 , если a > 0 , a ≠ 1 .
5. log a a p = p , при этом a > 0 , a ≠ 1 и p может быть любым действительным числом.
6. log a ( x · y ) = log a x + log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . В обобщенном виде это свойство можно представить как log a ( x 1 · x 2 · … · x n ) = log a x 1 + log a x 2 + … + log a x n , a > 0 , a ≠ 1 , x 1 > 0 , x 2 > 0 , … , x n > 0
7. ) log a x y = log a x — log a y .
8. log a x y = log a x — log a y , при этом a > 0 , a ≠ 1 , x > 0 , y > 0 .
9. log a x y = log a x — log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 .
10. log a b p = p · log a b , при этом a > 0 , a ≠ 1 , b > 0 , а p может быть любым действительным числом.
11. это свойство является следствием предыдущего: log a b n = 1 n · log a b , a > 0 , a ≠ 1 , n может быть любым натуральным числом больше 1 , b > 0 .
12. log a b = log c b log c a , при этом a > 0 , a ≠ 1 , b > 0 , c > 0 , c ≠ 1 .
13. свойство, также являющееся следствием: log a b = 1 log b a , где a > 0 , a ≠ 1 , b > 0 , b ≠ 1 .
14. log a q b p = p q · log a b , a > 0 , a ≠ 1 , b > 0 , p и q могут быть любыми действительными числами, q ≠ 0
15. log a q b p = p q , a > 0 , a ≠ 1 , p и q – любые действительные числа, q ≠ 0 .
16. log a q a p = p q , b log a c = c log a b , при этом a > 0 , a ≠ 1 , b > 0 , c > 0 .

Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что b n = b 1 n , если b ≥ 0 . Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия log a q b p = p q · log a b и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:

log a q b p = log a b p log a a q = p · log a b q = p q · log a b

То же относится и к последнему свойству из списка, выраженному формулой b log a c = C log a c = c log a b : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.

Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Как преобразовать числовое выражение с логарифмом

После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.

Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Как выбрать свойство логарифма для преобразования

Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.

Для начала преобразуем выражение, используя определение логарифма, выраженное формулой a log a b = b , a > 0 , a ≠ 1 , b > 0 .

Условие: преобразуйте и вычислите значение следующих выражений: 1 ) 5 log 5 4 ; 2 ) 10 lg ( 1 + 2 · π ) , 3 ) 2 + 3 log 2 + 3 ln 15 ; 4 ) 2 log 2 ( − 7 ) ; 5 ) ( — 5 ) log — 5 e 3

Решение

В первом примере прослеживается формула a log a b . У нас есть a = 5 , b = 4 , что соответствует необходимому условию a > 0 , a ≠ 1 , b > 0 . Используем нужное равенство a log a b = b и получим 5 log 5 4 = 4 .

Во втором случае a будет равно 10 , b – 1 + 2 · π . Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10 l g ( 1 + 2 · π ) = 1 + 2 · π .

В третьем выражении у нас есть степень вида a log a b , причем a = 2 + 3 и b = ln 15 . Запишем: 2 + 3 log 2 + 3 ln 15 = ln 15 . Хотя равенство также соответствует формуле a log a b , где a равно 2 , а b = — 7 , мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, — 7 не соответствует условию b > 0 , что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2 log 2 ( − 7 ) = − 7 будет ошибочна.

То же самое относится и к четвертому примеру. Мы не можем записать, что — 5 log — 5 · e 3 = e 3 , поскольку такое выражение смысла не имеет.

Ответ: 1 ) 5 log 5 4 = 4 ; 2 ) 10 l g ( 1 + 2 · π ) = 1 + 2 · π ; 3 ) 2 + 3 log 2 + 3 ln 15 = ln 15 ; 4 и 5 — не имеют смысла.

Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1 , имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма a log a b = b , a > 0 , a ≠ 1 , b > 0 , но в перевернутом виде, т.е. прочитанное справа налево, например, 3 = e ln 3 или 5 = 5 log 5 5 .

Далее возьмем примеры с другими свойствами логарифмов.

Условие: вычислите, если возможно: 1 ) log − 2 1 , 2 ) log 1 1 , 3 ) log 0 1 , 4 ) log 7 1 , 5 ) ln 1 , 6 ) l g 1 , 7 ) log 3 , 75 1 , 8 ) log 5 · π 71 .

Решение

В первых трех примерах мы видим не имеющие смысла выражения log − 2 1 , log 1 1 , log 0 1 . Основанием логарифма не может быть число меньше 1 , в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.

В других случаях логарифмы имеют подходящие основания: 7 , e , 10 , 3 , 75 и 5 · π 7 , а под знаками логарифма везде 1 . Зная соответствующее свойство логарифма ( log a 1 = 0 при любом a > 0 , a ≠ 1 ., мы можем сделать вывод, что значения этих выражений равны 0 .

Ответ: 1 , 2 , 3 смысла не имеют; 4 ) log 7 1 = 0 , 5 ) ln 1 = 0 , 6 ) l g 1 = 0 , 7 ) log 3 , 75 1 = 0 , 8 ) log 5 · e 7 1 = 0 .

Условие: вычислите значения: 1 ) log 1 3 1 3 , 2 ) ln e , 3 ) l g 10 , 4 ) log 5 · π 3 − 2 ( 5 · π 3 − 2 ) , 5 ) log − 3 ( − 3 ) , 6 ) log 1 1 .

Решение

Нам потребуется свойство логарифма, выраженное формулой log a a = 1 при a > 0 , a ≠ 1 . Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1 , 2 , 3 , 4 действительно ответом будет 1 , а вот в 5 и 6 исходные выражения смысла не имеют.

Ответ: 1 ) log 1 3 = 1 3 = 1 , 2 ) ln e = 1 , 3 ) l g 10 = 1 , 4 ) log 5 · π 3 − 2 ( 5 · π 3 − 2 ) = 1 ; 5 , 6 не имеют смысла.

Условие: вычислите: 1 ) log 3 3 11 , 2 ) log 1 + 2 2 ( 1 + 2 2 ) 7 2 3 , 3 ) log π 5 ( π 5 ) — 2 , 4 ) log − 10 ( − 10 ) 6 .

Решение

Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство log a a p = p , где a > 0 , a ≠ 1 и p будет любым действительным числом. С учетом этого можно записать следующее:

1. log 3 3 11 = 11
2. log 1 + 2 2 ( 1 + 2 · 2 ) 7 2 3 = 7 2 3
3. log π 5 ( π 5 ) — 2 = — 2
4. для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log − 10 ( − 10 ) 6 = 6 не имеет смысла.

Ответ: 1 ) log 3 3 11 = 11 , 2 ) log 1 + 2 2 ( 1 + 2 · 2 ) 7 2 3 = 7 2 3 , 3 ) log π 5 ( π 5 ) — 2 = — 2 , 4 ) не имеет смысла.

Условие: даны выражения log 2 , 6 4 · 1 2 7 , ln 2 + 1 π и l g ( ( − 5 ) · ( − 12 ) ) . Нужно представить их как суммы или разности логарифмов по тому же основанию.

Решение

Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: log a ( x · y ) = log a x + log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:

log 2 , 6 4 · 1 2 7 = log 2 , 6 4 + log 2 , 6 1 2 7

Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: log a x y = log a x — log a y , a > 0 , a ≠ 1 , x > 0 , y > 0 . Здесь в основании стоит положительное число e , также у нас есть положительный числитель 2 + 1 и знаменатель π , т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln 2 + 1 π = ln 2 + 1 — ln π .

Разберем третий пример. Начнем с того, что выражение l g ( ( − 5 ) · ( − 12 ) ) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа — 5 и — 12 отрицательны. Значит, преобразование l g ( ( − 5 ) · ( − 12 ) ) = l g ( − 5 ) + l g ( − 12 ) не подходит. Какое же свойство тогда использовать?

Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: l g ( ( − 5 ) · ( − 12 ) ) = l g ( 5 · 12 ) = l g 5 + l g 12 .

Ответ: 1 ) log 2 , 6 4 · 1 2 7 = log 2 , 6 4 + log 2 , 6 1 2 7 , 2 ) ln 2 + 1 π = ln 2 + 1 — ln π , 3 ) l g ( ( − 5 ) · ( − 12 ) ) = l g 5 + l g 12 .

Условие: упростите выражения log 3 0 , 25 + log 3 16 + log 3 0 , 5 и ln 2 3 — ln 1 3 .

Решение

Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log 30 , 25 + log 3 16 + log 3 0 , 5 = log 3 ( 0 , 25 · 16 · 0 , 5 ) = log 3 2 , а во втором ln 2 3 — ln 1 3 = ln 2 3 : 1 3 = ln 2 .

Ответ: 1 ) log 30 , 25 + log 3 16 + log 3 0 , 5 = log 3 ( 0 , 25 · 16 · 0 , 5 ) = log 3 2 , 2 ) ln 2 3 — ln 1 3 = ln 2 .

Условие: есть выражения log 0 , 7 5 11 , log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 и log 3 ( − 5 ) 6 . Нужно избавиться от степени в выражении под знаком логарифма.

Решение

Очевидно, что у нас здесь есть выражения вида log a b p . Берем свойство, которое выражается формулой вида

log a b p = p · log a b , где a > 0 , a ≠ 1 , b > 0 , p — любое действительное число. Поскольку условия a > 0 , a ≠ 1 , b > 0 выполнены, то мы можем преобразовать log a b p в произведение p · log a b .

1. в случае с первым выражением a равно 7 , b – пяти и p – 11 . Тогда log 0 , 7 5 11 = 11 · log 0 , 7 5 .
2. тут a = 3 — 1 , b = 3 — 2 + 5 · 67 3 , p = 5 + 1 . Нужные условия выполнены, значит, мы можем записать, что:
   log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 = = 5 + 1 · log 3 — 1 ( 3 — 2 + 5 · 67 3 )
3. у нас есть выражение той же структуры: log a b p , a = 3 , b = − 5 , p = 6 , однако одно из условий не выполняется, а именно b у нас меньше 0 . Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log 3 ( − 5 ) 6 = log 3 5 6 = 6 · log 3 5 .

Ответ: 1 ) log 0 , 7 5 11 = 11 · log 0 , 7 5 , 2 ) log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 5 + 1 = = 5 + 1 · log 3 — 1 ( 3 — 2 + 5 · 67 3 ) 3 ) log 3 ( − 5 ) 6 = 6 · log 3 5 .

Применение формулы в обратном порядке в виде p · log a b = log a b p требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3 · ln 5 = ln 5 3 и l g 2 · log 2 3 = log 2 3 l g 2 .

Условие: согласно таблице логарифмов, l g 2 ≈ 0 , 3010 и l g 5 ≈ 0 , 6990 . Вычислите, сколько будет log 2 5 . Здесь же: запишите ln 11 ln 3 в виде логарифма, основание которого равно 3 .

Решение

Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.

log 2 5 = l g 5 l g 2

Вычисляем и находим ответ: l g 5 l g 2 ≈ 0 , 6990 0 , 3010 ≈ 2 , 3223 .

Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. log c b log c a = log a b .

Считаем: ln 11 ln 3 = log 3 11

Ответ: 1 ) log 2 5 ≈ 2 , 3223 , 2 ) ln 11 ln 3 = log 3 11 .

Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.

Условие: 1 ) дан логарифм ln 1 + π 7 . Необходимо избавиться от корня под знаком логарифма; 2 ) выполните преобразование дроби 1 log 2 5 в логарифм с основанием 4 ; 3 ) преобразуйте логарифм log e 2 3 4 5 так, чтобы избавиться от степени в основании; 4 ) вычислите, сколько будет log 2 — 1 3 2 1 6 ; 5 ) осуществите замену 2 , 3 log 7 3 на степень с основанием 3 .

Решение

1. Вспоминаем следствие из свойства логарифма степени, которое выражается формулой log a b n = 1 n · log a b .В первом случае можем сразу же подсчитать: ln 1 + π 7 = 1 7 · ln ( 1 + π ) .
2. во втором случае нам понадобится формула log a b = 1 log b a , примененная в обратном порядке. Получим 1 log 2 5 = log 5 2 .
3. здесь нам потребуется свойство log a q b p = p q · log a b . Применяем его и получаем log e 2 3 4 5 = 4 5 2 · ln 3 = 2 5 · ln 3 .
4. в этом случае нам нужно будет следствие, выраженное формулой log a q a p = p q : log ( 2 ) — 1 3 2 1 6 = 1 6 — 1 3 = — 1 2
5. используем формулу свойства b log a c = c log a b и вычисляем ответ:

2 , 3 log 7 · 3 = 3 log 7 2 , 3

Ответ: 1 ) ln 1 + π 7 = 1 7 · ln ( 1 + π ) ; 2 ) 1 log 2 5 = log 5 2 ; 3 ) log e 2 3 4 5 = 2 5 · ln 3 ; 4 ) log ( 2 ) — 1 3 2 1 6 = — 1 2 . 5 ) 2 , 3 log 7 · 3 = 3 log 7 2 , 3 .

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Задачи с применением нескольких свойств логарифмов

В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.

Условие: вычислите, сколько будет ( log 3 15 − log 3 5 ) · 7 log 7 5 .

Решение

Мы можем заменить выражение в скобках логарифмом log 3 ( 15 : 5 ) , используя свойство частного. Вычисляем его значение и получаем log 3 ( 15 : 5 ) = log 3 3 = 1 .

Согласно основному определению логарифма, значением 7 log 7 5 будет 5 . Подставим в исходное выражение получившиеся результаты и найдем, что ( log 3 15 − log 3 5 ) · 7 log 7 5 = 1 · 5 = 5 .

Вот все решение без комментариев:

( log 3 15 − log 3 5 ) · 7 log 7 5 = log 3 ( 15 : 5 ) · 5 = = log 3 3 · 5 = 1 · 5 = 5

Ответ: ( log 3 15 − log 3 5 ) · 7 log 7 5 = 5 .

Условие: вычислите, чему равен log 3 log 2 2 3 − 1 .

Решение

Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log 2 2 3 = 3 . Получим, что log 3 log 2 2 3 = log 3 3 , а дальше log 3 3 = 1 . Следовательно, log 3 log 2 2 3 − 1 = 1 − 1 = 0 .

Ответ: log 3 log 2 2 3 − 1 = 0 .

Условие: выполните упрощение выражения 3 ln 5 ln 3 log 5 2 .

Решение

Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5 ln 3 как log 3 5 . У нас получилось 3 log 3 5 log 5 2 . Теперь применяем формулу основного определения логарифма 3 log 3 5 = 5 и получаем, что 3 log 3 5 log 5 2 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2 .

Ответ: 3 ln 5 ln 3 log 5 2 = 2 .

Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log 3 3 4 , 5 2 + log 5 3 , lg 0 , 01 . Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 5 2 + log 5 3 = 5 2 · 5 log 5 3 = 25 · 3 = 75 , log 3 3 4 = log 3 1 2 3 4 = 4 1 2 = 8 и l g 0 , 01 = l g 10 − 2 = − 2 . Разберем подробнее, как именно это делается.

Видео:10 класс. Алгебра. Преобразование логарифмических выражений.Скачать

Предварительное преобразование перед применением основных свойств логарифмов

На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.

В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.

Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.

1. Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln 2 5 3 2 3 32 , log 3 81 .
2. Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2 log 2 2 3 , 3 2 · log 35 , 7 1 + log 74 , 25 ( log 3 5 ) — 3 и др.
3. Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log 1 5 ( 0 , 2 ) 7
4. Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде l g ( − 3 ) − 4 , log 6 ( ( − 9 ) · ( − 4 ) ) и др.

Разберем подробно каждый вид преобразования.

Видео:ЕГЭ-2022.Профиль. Задание-4. Логарифмические выраженияСкачать

Как выделить степень в основании логарифма и под его знаком

Сразу возьмем конкретный пример. У нас есть выражение log 1 9 81 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 1 9 . Их легко представить в виде степени с основанием 3 : 81 = 3 4 и 1 9 = 3 − 2 . Значит, все выражение можно переписать как log 3 — 2 3 4 , а здесь уже видна возможность использования свойства log a q b p = p q · log a b . Таким образом, log 1 9 81 = log 3 — 2 = 4 — 2 = — 2 .

Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.

В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3 , которые легко узнать с первого взгляда: 243 = 3 5 , 81 = 3 4 , 8 = 2 3 , 64 = 2 6 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10 , чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10 , 100 и др.

Условие: вычислите или упростите выражения log 6 216 , log 343 1 243 , log 0 , 000001 0 , 001 .

Решение

1. В первом случае мы сразу видим, что 216 можно представить в виде 6 3 . Значит, log 6 216 = log 6 6 3 = 3 .
2. у нас есть числа 343 и 1 243 . Обратимся к таблице степеней и увидим, что их можно представить в виде 7 3 и 3 − 4 . Выполняем дальнейшие преобразования и получаем:
   log 343 1 243 = log 7 3 3 — 4 = = — 4 3 · log 7 3 = — 1 1 3 · log 7 3
3. Поскольку 0 , 000001 = 10 − 6 и 0 , 001 = 10 − 3 , тогда log 0 , 000001 0 , 001 = log 10 − 6 10 − 3 = — 3 — 6 = 1 2

Ответ: 1 ) log 6 216 = 3 , 2 ) log 343 1 243 = — 1 1 3 · log 7 3 ; 3 ) log 0 , 000001 0 , 001 = 1 2 .

Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.

Условие: упростите выражение log 3 648 · log 2 3 .

Решение

Выполняем разложение 648 на простые множители.

648 324 162 81 9 3 1 2 2 2 3 3 3

Значит, это число можно представить в виде 648 = 2 3 · 3 4 . Следовательно, log 3 648 · log 2 3 = log 3 ( 2 3 · 3 4 ) · log 2 3

Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.

log 3 ( 2 3 · 3 4 ) · log 2 3 = ( log 3 2 3 + log 3 3 4 ) · log 2 3 = = ( 3 · log 3 2 + 4 ) · log 2 3 .

Упрощаем выражение через раскрытие скобок:

( 3 · log 3 2 + 4 ) · log 2 3 = 3 · log 3 2 · log 2 3 + 4 · log 2 3 .

В полученном выражении log 3 2 · log 2 3 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3 · log 3 2 · log 2 3 + 4 · log 2 3 = 3 · 1 + 4 · log 2 3 = 3 + 4 · log 2 3 .

Ответ: log 3 648 · log 2 3 = 3 + 4 · log 2 3 .

Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 3 2 3 · 3 — 2 , 2 · 2 2 7 3 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.

Условие: найдите значение выражений log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 и log 3 729 1 9 .

Решение

В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 5 2 · 5 − 0 , 5 · 5 − 1 = 5 2 − 0 , 5 − 1 = 5 0 , 5 . Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:

5 3 4 5 4 = 5 3 4 4 = 5 3 4 — 4 = 5 — 3 1 4

Полученное выражение подставим в исходный логарифм, применив формулу log a q a q = p q , и получим ответ:

log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 = log 5 0 . 5 5 — 3 1 4 = — 3 1 4 0 . 5 = = — 13 4 1 2 = — 13 2 = — 6 1 2

Во втором случае представим число 729 как 3 6 , а 1 9 как 3 − 2 . Исходный логарифм приобретет вид log 3 3 6 3 — 2 . Используя свойство корня из степени, преобразуем основание логарифма и получим:

3 3 6 = 3 3 3 = 3 1 — 3 = 3 — 2

Заканчиваем преобразование: log 3 3 6 3 — 2 = log 3 — 2 3 — 2 = 1 .

Ответ: 1 ) log 5 2 · 5 — 0 . 5 · 5 — 1 5 3 4 5 4 = — 6 1 2 ; 2 ) log 3 729 1 9 = 1

Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.

Условие: вычислите значения log 1 3 — 1 1 32 · 3 + 1 — 5 и log 2 · cos 1 ( 1 + cos 2 ) 3 .

Решение

Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:

1 3 — 1 = 3 + 1 3 — 1 · 3 + 1 = 3 + 1 3 2 — 1 2 = 3 + 1 2

Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:

1 32 · 3 + 1 — 5 = 3 + 1 5 32 = 3 + 1 5 2 5 = 3 + 1 2 5

В результате преобразований у нас получился логарифм степени основания log 3 + 1 2 3 + 1 3 5 . Значение данного выражения будет равно 5 .

Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos 2 a = 1 + cos 2 a 2 :

log 2 · cos 1 ( 1 + cos 2 ) 3 = log 2 · cos 1 ( 2 · cos 2 1 ) 3

Преобразуем второй логарифм, записав его как степень 2 · cos 2 1 1 2 или же 2 · cos 1 2 3 = 2 · cos 1 6 . Оба выражения будут иметь одно и то же значение, равное шести.

Ответ: 1 ) log 1 3 — 1 1 32 · 3 + 1 — 5 = 5 ; 2 ) log 2 · cos 1 ( 1 + cos 2 ) 3 = 6 .

Видео:БАЗА. Показательные и логарифмические выражения и уравненияСкачать

Как применять свойства степени при преобразовании выражений с логарифмами

Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.

Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями a p · a q = a p + q . Чаще всего его применяют в обратном порядке, т.е. справа налево.

Условие: вычислите значения 3 − 2 + log 3 7 и 0 , 7 2 − log 0 , 7 0 , 1 .

Решение

В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3 − 2 + log 3 7 = 3 − 2 · 3 log 3 7 . Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:

3 − 2 · 3 log 3 7 = ( 1 9 ) · 7 = 7 9

Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0 , 7 2 − log 0 , 7 0 , 1 = 0 , 7 2 · 0 , 7 − log 0 , 7 0 , 1 . После этого нам нужно представить показатель − log 0 , 7 0 , 1 в виде l log 0 , 7 ( 0 , 1 ) − 1 = log 0 , 7 10 . Теперь все, что нам осталось, – это закончить вычисления:

0 , 7 2 · 0 , 7 − log 0 , 7 0 , 1 = 0 , 49 · 0 , 7 log 0 , 7 10 = 0 , 49 · 10 = 4 , 9

Ответ: 1 ) 3 − 2 + log 3 7 = 7 9 ; 2 ) 0 , 7 2 − log 0 , 7 0 , 1 = 4 , 9 .

Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой ( a p ) q = a p · q , например, если у нас есть выражение ( e ln 2 ) 3 , то мы можем заключить, что значение части в скобках будет равно 2 . Значит, ( e ln 2 ) 3 = 2 3 = 8 . А если в условии указано ( e 3 ) ln 2 или ( e 3 ) ln 2 , то мы сначала приводим их к виду ( e ln 2 ) 3 :

e 3 · ln 2 = e ln 2 · 3 = ( e ln 2 ) 3 и ( e 3 ) ln 2 = e 3 · ln 2 = e ln 2 · 3 = ( e ln 2 ) 3 .

Посмотрим пример решения такой задачи.

Условие: выполните упрощение выражений 2 log 2 2 3 − 3 log 2 3 и 5 ( log 8 5 ) − 1 .

Решение

Отметим, что выражения 2 log 2 2 3 и 2 log 2 2 3 не являются равными друг другу. Мы можем представить 2 log 2 2 3 как 2 log 2 3 · log 2 3 . Используя свойство степени, представим его как ( 2 log 2 3 ) log 2 3 , что будет тождественно равным 3 log 2 3 . В итоге мы имеем, что 2 log 2 2 3 − 3 log 2 3 = 3 log 2 3 − 3 log 2 3 = 0 .

Вот запись всего решения:

2 log 2 2 3 − 3 log 2 3 = 2 log 2 3 · log 2 3 − 3 log 2 3 = = ( 2 log 2 3 ) log 2 3 − 3 log 2 3 = 3 log 2 3 − 3 log 2 3 = 0

Перейдем ко второму примеру. Запись 25 ( log 8 5 ) — 1 не будет равна ( 25 log 8 5 ) − 1 . Мы можем представить степень ( log 8 5 ) − 1 как дробь 1 log 8 5 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле log a b = 1 log b a , чтобы получить log 5 8 .

Так, 25 ( log 8 5 ) — 1 = 25 log 5 8 . Поскольку 25 – это 5 2 , имеем 5 log 5 8 = ( 5 2 ) log 5 8 . То, что у нас получилось, представляем в виде ( 5 log 5 8 ) . Нам осталось только вычислить значение: ( 5 log 5 8 ) 2 = 8 2 = 64 .

Ответ: 1 ) 2 log 2 2 3 − 3 log 2 3 = 0 , 2 ) 25 ( log 8 5 ) − 1 = 64 .

Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,

4 − 0 , 5 + 2 · log 4 3 = 4 − 0 , 5 · 4 2 · log 4 3 = = 1 2 · ( 4 log 4 3 ) 2 = 1 2 · 3 2 = 1 2 · 9 = 4 , 5

Видео:Показательные и логарифмические уравнения №12, 14 | Профильная математика ЕГЭ 2022 | УмскулСкачать

Преобразование логарифмов с десятичными дробями

Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log 0 , 4 2 5 3 ? Отметим, что 2 5 и 0 , 4 равны между собой 0 , 4 = 4 10 = 2 5 , то есть это разные формы записи для одного и то же числа.

В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.

Разберем подобную задачу.

Условие: вычислите значение выражения log 0 , 4 6 , 25 .

Решение

Начнем с перехода от десятичных дробей к обыкновенным.

log 0 , 4 6 , 25 = log 4 10 625 100 = log 2 5 25 4

Теперь видно, что мы можем преобразовать 25 4 в виде ( 2 5 ) − 2 и воспользоваться формулой логарифма степени. Вычисляем значение:

log 2 5 25 4 = log 2 5 2 5 — 2 = — 2

Ответ: — 2 .

Видео:Преобразование логарифмических выражений.Скачать

Преобразование выражений с отрицательными числами под знаком логарифма

Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log 3 — 9 3 — 27 или log 3 ( ( − 2 ) · ( − 5 ) ) .

Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log 3 ( ( − 2 ) · ( − 5 ) ) к log 3 ( − 2 ) + log 3 ( − 5 ) , применить свойство логарифма степени к log 2 ( − 2 ) 6 или логарифма частного к log 3 — 9 3 — 27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.

Что это значит на практике? Вернемся к нашему примеру log 3 ( ( − 2 ) · ( − 5 ) ) . Структура выражения соответствует формуле log a ( x · y ) , где a равно 3 , x — 3 и y — 5 . Поскольку условия a > 0 , a ≠ 1 , x > 0 , y > 0 не выполнены, формулу log a ( x · y ) = log a x + log a y мы применить не можем, и равенство log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 ( − 2 ) + log 3 ( − 5 ) записать нельзя. Преобразования вида log 3 — 9 3 — 27 = log 3 — 9 3 — log 3 ( — 27 ) также будут неправильными.

Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0 .

Вернемся опять к нашему примеру. Согласно правилам умножения, ( − 2 ) · ( − 5 ) = 2 · 5 , значит, log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 ( 2 · 5 ) . К выражению в таком виде мы уже можем применить формулу log 3 ( 2 · 5 ) = log 3 2 + log 3 5 . А вот для примера log 2 ( − 2 ) 6 нужно будет выполнить следующие действия:

( − 2 ) 6 = ( ( − 1 ) · 2 ) 6 = ( − 1 ) 6 · 2 6 = 1 · 2 6 = 2 6

Значит, log 2 ( − 2 ) 6 = log 2 2 6 = 6 .

Условие: найдите значение выражения log 2 — 16 3 — 2 — 2 3 .

Решение

Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.

Определив корень нечетной степени из отрицательного числа, выполним переход от — 16 3 — 2 — 2 3 к — 16 3 — 2 — 2 3 . Согласно правилам деления, получим — 16 3 — 2 — 2 3 = 16 3 2 — 2 3 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.

16 3 2 — 2 3 = 2 4 3 2 — 2 3 = 2 4 3 2 — 2 3 = 2 4 3 — — 2 3 = 2 2 log 2 — 16 3 — 2 — 2 3 = log 2 2 2 = 2

Ответ: log 2 — 16 3 — 2 — 2 3 = 2 .

Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как log a ( x · y ) = log a | x | + log a | y | , где a > 0 , a ≠ 1 , x ≠ 0 , y ≠ 0 , то после преобразования мы получим log 3 ( ( − 2 ) · ( − 5 ) ) = log 3 | − 2 | + log 3 | − 5 | = log 3 2 + log 3 5 .

Видео:10 класс. Алгебра. Преобразование логарифмических выражений.Скачать

Как преобразовать логарифмическое выражение с переменными

В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.

Видео:10 класс. Алгебра. Преобразование логарифмических выражений.Скачать

Особенности преобразований выражений с переменными

Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.

У нас есть логарифмическое выражение log 2 ( x + 1 ) 4 . При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством ( x + 1 ) 4 > 0 , значение которого является числовым множеством ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Решить его можно с помощью метода интервалов.

Исходное выражение соответствует формуле log A B p , где A равно 2 , B – x + 1 , а p – четырем.

Мы видим, что заданное выражение соответствует виду log A B p , где A = 2 , B = x + 1 и p = 4 . Такие выражения преобразовываются по свойству логарифма степени log a b p = p · log a b . Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x = − 2 . В итоге: log 2 ( − 2 + 1 ) 4 = log 2 1 = 0 , а 4 · log 2 ( − 2 + 1 ) = 4 · log 2 ( − 1 ) –выражение, не имеющее смысла. Значит, мы ошиблись.

Причина ошибки в том, что мы взяли формулу log a b p = p · log a b , но это допустимо лишь при условии a > 0 , a ≠ 1 , b > 0 , p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x + 1 > 0 , что аналогично x > − 1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x > − 1 , но и из промежутка x − 1 . Но для x − 1 мы не имели права осуществлять преобразование по выбранной формуле.

Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Почему надо учитывать область допустимых значений

Продолжая работу с выражением log 2 ( x + 1 ) 4 , проанализируем, как изменится область значений, когда мы выполним переход к виду 4 · log 2 ( x + 1 ) . Ранее мы уже определили эту область как множество ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Теперь вычислим, какова будет область допустимых значений для 4 · log 2 ( x + 1 ) . Она определяется условием x + 1 > 0 , а ему, в свою очередь, будет отвечать множество ( − 1 , + ∞ ) . Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.

Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.

Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.

Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:

1. когда мы переходим от логарифма произведения к сумме, например, ln ( x · ( x + 3 ) ) = ln x + ln ( x + 3 ) сузит нужную область.
2. Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log 2 x sin x на log 2 x − log 2 sin x .
3. Когда мы выносим четный показатель степени, используя формулу логарифма степени log a b p = p · log a b и формулу log a b p = p q · log a b . Примеры таких преобразований – log x 3 ( x — 8 ) 2 = 2 3 · log x ( x — 8 ) , ln ( x + 3 ) − 4 = − 4 · ln ( x + 3 ) .

Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4 · log 2 ( x + 1 ) к log 2 ( x + 1 ) 4 . В этом случае область расширяется от ( − 1 , + ∞ ) до ( − ∞ , − 1 ) ∪ ( − 1 , + ∞ ) . Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4 · log 2 ( x + 1 ) = log 2 ( x + 1 ) 4 имеет место на области значений переменной x для исходного выражения 4 · log 2 ( x + 1 ) , то есть, при x + 1 > 0 , что аналогично ( − 1 , + ∞ ) .

Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.

Видео:4 Задание | Преобразование логарифмических выраженийСкачать

Правила проведения преобразований

Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.

Условие: упростите 3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 .

Решение

На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.

Чтобы перейти от l g ( x + 2 ) 7 к 7 · l g ( x + 2 ) и от l g ( x + 2 ) 4 к 4 · l g ( x + 2 ) , нам нужно, чтобы x + 2 > 0 . Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств ( x + 2 ) 7 > 0 , x + 2 > 0 , ( x + 2 ) 4 > 0 , которая будет равносильной условию x + 2 > 0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:

3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 = = 3 · 7 · l g ( x + 2 ) − l g ( x + 2 ) − 5 · 4 · l g ( x + 2 ) = = 21 · l g ( x + 2 ) − l g ( x + 2 ) − 20 · l g ( x + 2 ) = = ( 21 − 1 − 20 ) · l g ( x + 2 ) = 0

Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:

3 · l g ( x + 2 ) 7 — l g ( x + 2 ) — 5 · l g ( x + 2 ) 4 = = l g ( ( x + 2 ) 7 ) 3 — l g ( x + 2 ) — l g ( ( x + 2 ) 4 ) 5 = = l g ( x + 2 ) 21 — l g ( x + 2 ) — l g ( x + 2 ) 20 = = l g ( x + 2 ) 21 ( x + 2 ) · ( x + 2 ) 20 = l g 1 = 0

Ответ: 3 · l g ( x + 2 ) 7 − l g ( x + 2 ) − 5 · l g ( x + 2 ) 4 = 0 .

А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.

Условие: выполнить упрощение выражения l g ( x + 2 ) 4 − l g ( x + 2 ) 2 .

Решение

Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x > − 2 и x − 2 . Если x > − 2 , то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: l g ( x + 2 ) 4 − l g ( x + 2 ) 2 = 4 · l g ( x + 2 ) − 2 · l g ( x + 2 ) = 2 · l g ( x + 2 ) . Однако в области значений есть и промежуток x + 2 0 , и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?

Применим знаки модуля. Вспомним определение данного понятия и представим x + 2 при x + 2 0 как − | x + 2 | . В таком случае мы можем выполнить переход от l g ( x + 2 ) 4 − l g ( x + 2 ) 2 к l g ( − | x + 2 | ) 4 − l g ( − | x + 2 | ) 2 , и далее к l g | x + 2 | 4 − l g | x + 2 | 2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь | x + 2 | > 0 при любом x .

Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при | x + 2 | 0 , имеем 2 · l g | x + 2 | = 2 · l g ( − ( x + 2 ) ) . Это и будет ответом на поставленный вопрос.

Ответ: l g ( x + 2 ) 4 — l g ( x + 2 ) 2 = 2 · l g ( x + 2 ) , x + 2 > 0 2 · l g ( — ( x + 2 ) ) , x + 2 0 . Можно записать ответ компактнее, используя знаки модуля: l g ( x + 2 ) 4 — l g ( x + 2 ) 2 = 2 · l g x + 2 .

Возьмем еще один пример, чтобы закрепить навыки работы с модулями.

Условие: представьте выражение ln x — 1 · x — 2 x — 3 как сумму и разность логарифмов линейных двучленов x − 1 , x − 2 и x − 3 .

Решение

Вычисляем область допустимых значений данного выражения:

x — 1 · x — 2 x — 2 > 0 , ( 1 , 2 ) ∪ 3 , + ∞

Поскольку значения x − 1 , x − 2 и x − 3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:

ln x — 1 · x — 2 x — 3 = = ln ( x — 1 ) + ln ( x — 2 ) — ln ( x — 3 )

А на интервале от одного до двух значение x − 1 будет положительным, а x − 2 и x − 3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:

ln x — 1 · x — 2 x — 3 = ln x — 1 · — x — 2 — x — 3 = = ln ( x — 1 ) · x — 2 x — 3

После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x − 1 , | x − 2 | и | x − 3 | будут положительными. В итоге имеем:

ln x — 1 · x — 2 x — 3 = ln ( x — 1 ) + ln x — 2 — ln x — 3 = = ln x — 1 + ln ( — ( x — 2 ) ) — ln ( — ( x — 3 ) )

Теперь объединяем получившиеся результаты.

Ответ: ln x — 1 · x — 2 x — 3 = ln x — 1 + ln ( — ( x — 2 ) ) — ln ( — ( x — 3 ) )

С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:

1. сумма логарифмов log a | X | + log a | Y | , a > 0 , a ≠ 1 может быть использована вместо логарифма произведения log a ( X · Y ) .
2. Разность логарифмов log a | X | − log a | Y | , где a > 0 , a ≠ 1 , X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
3. Выражение p · log a | B | , где a > 0 , a ≠ 1 , p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p .

Условие: выполните упрощение выражения 13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 .

Решение

На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:

( x + 4 ) · ( x — 2 ) > 0 , ( x + 4 ) 13 x — 2 > 0 — ∞ , — 4 ∪ 2 , + ∞

У нас получилось, что значения выражений x + 4 , x − 2 и ( x + 4 ) 13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.

13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 ( x + 4 ) 13 x — 2 = = 13 · log 8 x + 4 + 13 · log 8 x — 2 — — log 8 x + 4 13 — log 8 x — 2 = = 13 · log 8 x + 4 + 13 · log 8 x — 2 — — log 8 ( x + 14 ) 13 + log 8 x — 2 = = 13 · log 8 x + 4 — log 8 ( x + 4 ) 13 + 14 · log 8 x — 2

Зная свойства модуля, перепишем x + 4 13 в виде x + 4 13 . Значит, что:

13 · log 8 x + 4 — log 8 ( x + 4 ) 13 + 14 · log 8 x — 2 = = 13 · log 8 x + 4 — log 8 x + 4 13 + 14 · log 8 x — 2

Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:

13 · log 8 x + 4 — log 8 x + 4 13 + 14 · log 8 x — 2 = = 13 · log 8 x + 4 — 13 · log 8 x + 4 + 14 · log 8 x — 2 = = 14 · log 8 x — 2

Возможны и другие преобразования, которые дают тот же результат:

13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 = = log 8 ( ( x + 4 ) · ( x — 2 ) ) 13 — log 8 x + 4 13 x — 2 = = log 8 ( ( x + 4 ) 13 · ( x — 2 ) ) 13 — log 8 x + 4 13 x — 2 = = log 8 ( x + 4 ) 13 · ( x — 2 ) 13 x + 4 13 x — 2 = log 8 ( x — 2 ) 14

Поскольку на области допустимых значений x − 2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log 8 ( x — 2 ) 14 = 14 · log 8 x — 2

А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14 · log 8 ( x − 2 ) , который был бы верен при x ∈ ( 2 , + ∞ ) , однако ошибочен на всей остальной области допустимых значений.

Ответ: 13 · log 8 ( ( x + 4 ) · ( x — 2 ) ) — log 8 x + 4 13 x — 2 = 14 · log 8 x — 2 .