- Функция называется линейной, если ее можно записать в виде (y=kx+b), где (k) и (b) -некоторые числа.
- График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
- Как меняется график при разных (k)?
- При любом (k>0) функция возрастает и при любом (k модуль (k), тем «круче» график.
- Как по графику определить коэффициент k?
- Как меняется график при разных значениях (b)?
- Присоединяйтесь к нашей группе ВКонтакте
- Смотрите нас в YouTube
- Линейная функция, ее свойства и график
- теория по математике 📈 функции
- Свойства линейной функции
- Пример №1
- Пример №2.
- Пример №3
- Коэффициенты k и b
- Содержание
- Коэффициент b
- Частные случаи. b = 0
- 📺 Видео
Функция называется линейной, если ее можно записать в виде (y=kx+b), где (k) и (b) -некоторые числа.
Функция не всегда сразу задана в виде (y=kx+b), иногда такой вид получится только после преобразований. Например, (y=6(x-1)+10x) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим (y=16x-6).
График линейной функции всегда представляет собой прямую линию – отсюда и название: «линейная функция».
Чтобы в этом убедиться построим графики функций (y=2x), (y=fracx-5), (y=8).


Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Видео:Занятие 1. График линейной функции y=kx+bСкачать

Как меняется график при разных (k)?
Чтобы определить, как влияет на график коэффициент (k), построим несколько функций разными (k): (frac),(-frac),(2),(-2) и (0). При этом во всех функциях сделаем (b) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: (y=fracx), (y=-fracx), (y=2x), (y=-2x), (y=0).
Заметьте, что при (k=2) и (frac) — функция возрастает, а при (k=-2) и (-frac) — убывает. На самом деле:
При любом (k>0) функция возрастает и при любом (k модуль (k), тем «круче» график.
Видео:Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента (k) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение (k) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях (|k|=frac). То есть на первом графике (k=2),а на втором (k=-frac).
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Как меняется график при разных значениях (b)?
Чтобы определить, как (b) влияет на график, построим несколько функций с разными (b): (6), (2), (0), (-3) и (-8). При этом (k) пусть во всех функциях будет равен (2).
Не сложно заметить, что прямая либо поднимается на (b) (если (b>0)) либо опускается на (|b|) если
((b 0),(b>0)
B. — функция возрастает — (k>0). Точка пересечения оси (y) и прямой находится выше нуля, значит (b>0). Подходит вариант под цифрой 1).
Отмечаем точку (b) на оси игреков.
От неё идем вправо на количество клеточек равное знаменателю (k), и вверх на количество клеточек равное числителю (k) (если (k>0)) или вниз на тоже количество (если (k 0). Поэтому идем вправо на единицу и вверх на (3). Ставим точку.
Проводим через эти две точки прямую.



Пример: Построить график функции (y=-frac x-3).
(b=-3) отмечаем точку с этим значением на оси (y).
(k=-frac), (k
Присоединяйтесь к нашей группе ВКонтакте
Смотрите нас в YouTube
Видео:Линейная функция и её график. Алгебра, 7 классСкачать

Линейная функция, ее свойства и график
теория по математике 📈 функции
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Видео:ГРАФИК ФУНКЦИИ y = kx + b | линейная функция | 7 классСкачать

Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
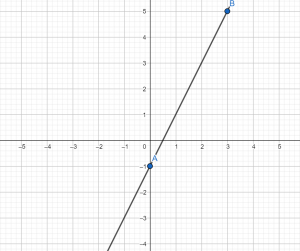
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
| х |
| у |
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
| х | 0 | 3 |
| у |
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2 × 0 – 1= –1;
у=2х – 1=2 × 3 – 1= 5.
Вписываем в таблицу значения у:
| х | 0 | 3 |
| у | –1 | 5 |
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5),
Проводимость — способность живой ткани проводить возбуждение.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
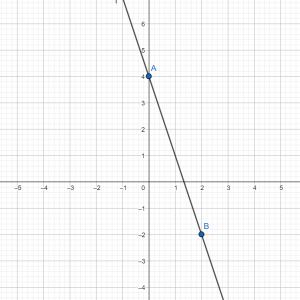
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
| х | 0 | 2 |
| у | 4 | –2 |
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
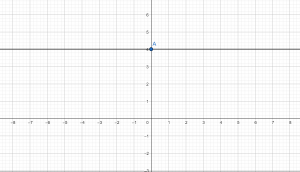
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
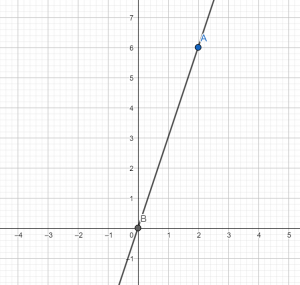
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
График данной функции зависит от k и b.
- если k 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Вариант 51, № 7. Нахождение k и b линейной функции y=kx+b. Пример 1Скачать

Коэффициенты k и b
Видео:Линейная функция и ее график. 7 класс.Скачать

Содержание
Положение прямой на графике зависит от величины коэффициентов $k$ и $b$
Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$
При $k > 0$ угол между графиком и осью $Ox$ меньше $90 degree$ (острый)
При $k
Видео:Задание 5 Знаки коэффициентов k и b в формуле линейной функции y=kx+bСкачать

Коэффициент b
Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.
Другими словами, коэффициент $b$ показывает, насколько график сдвинут вдоль оси $Oy$. Если $b > 0$, то график будет сдвинут вверх, и если $b
Так на нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).
График функции $y=50x + 500$
Видео:ЛИНЕЙНАЯ ФУНКЦИЯ | 7 класс Макарычев | график функции y=kx+bСкачать

Частные случаи. b = 0
В случае, когда коэффициент $b = 0$, а функция прямо пропорциональна, ее график будет проходить через начало координат $O(0;0)$. Ведь при подставлении в формулу $x = 0$ получим и $y = 0$.
Для построения графика такой функции достаточно найти одну точку, вторая – начало координат $О(0;0)$.
Важно: график в виде вертикальной прямой, параллельной оси $Oy$, не является графиком функции. В таком случае одному значению аргумента соответствует множество значений $y$. Это не наш случай, потому что он не соответствует самому определению функции.
При этом прямой, параллельной оси $Ox$, график функции может быть. Это возможно, когда коэффициент $k = 0$. Угол наклона также будет равен $0$. Формула принимает вид $y = b$.
📺 Видео
Линейное уравнение с двумя переменными. 7 класс.Скачать

Алгебра 7 класс. 29 сентября. Построить график линейного уравненияСкачать

Алгебра 7 Линейная функция y=kxСкачать

ФУНКЦИЯ алгебра 7 класс ГРАФИК ФУНКЦИИ МакарычевСкачать

Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать

Линейная функция. Нахождение формулы линейной функцииСкачать

Линейная функция y=k*x+b. Значение коэффициентов k и b в линейной функции.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Функция y=k/x и ее график. 7 класс.Скачать

ЛИНЕЙНАЯ ФУНКЦИЯ. §23 Алгебра 7 классСкачать