Предположим что уравнение бюджетной линии задано в виде (4 видео)

Содержание

Глава 2 — БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ
Рабочая программа (стр. 3 )
Бюджетная линия: понятие, уравнение, пример и график
Уравнение бюджетного ограничения
Пример
📹 Видео

Видео:Микроэкономика. Урок 21. Бюджетная линияСкачать

Глава 2 — БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ

Экономическая теория поведения потребителя очень проста: экономисты полагают, что потребители выбирают лучший товарный набор, который могут себе позволить. Чтобы наполнить эту теорию конкретным содержанием, мы должны более точно описать, что именно подразумевается под «лучшим» и что именно подразумевается под «могут себе позволить». В настоящей главе сосредоточимся на изучении описания того, что потребитель может себе позволить, а в следующей главе — на концепции определения потребителем того, что является «лучшим». После этого мы сможем приступить к детальному изучению значения этой простой модели поведения потребителя.

2.1. Бюджетное ограничение

Начнем с рассмотрения понятия бюджетного ограничения. Предположим, что имеется некое множество товаров, в пределах которого потребитель может осуществлять свой выбор. В реальной жизни существует много товаров, выступающих объектами потребления, однако для наших целей удобно рассмотреть случай всего двух товаров, поскольку тогда можно описать поведение потребителя в отношении выбора товаров графически.

Обозначим потребительский набор данного потребителя через (х₁, х₂). Это просто два числа, говорящие нам о том, сколько товара 1, х₁, и сколько товара 2, х₂, хочет потребить данный потребитель. Иногда удобно обозначать потребительский набор лишь одним символом, скажем, X, где X — просто сокращенное обозначение указанного перечня двух чисел (х₁, х₂).

Предположим, что из наблюдений нам известны цены этих двух товаров, (р₁, р₂), и та сумма денег, которую может израсходовать потребитель, m. Тогда бюджетное ограничение потребителя может быть записано в виде

Здесь р₁х₁ — сумма денег, расходуемая потребителем на товар 1, а р₂х₂ — сумма денег, расходуемая им на товар 2. Бюджетное ограничение потребителя требует, чтобы сумма денег, затраченная на оба товара, не превышала общей суммы денег, которую может израсходовать данный потребитель. Доступными для потребителя наборами являются те, которые стоят не дороже m. Мы называем это множество доступных потребительских наборов при ценах (р₁, р₂) и доходе m бюджетным множеством данного потребителя.

2.2. Двух товаров зачастую вполне достаточно

Предпосылка о наличии всего лишь двух товаров носит более общий характер, чем можно было бы поначалу подумать, поскольку часто можно считать один из товаров представляющим все другие товары, которые потребитель мог бы захотеть потребить.

Например, если мы хотим изучить спрос потребителя на молоко, мы можем обозначить через х₁ его ежемесячное потребление молока в квартах, а через х₂ — все остальные товары, которые мог бы захотеть потребить данный потребитель.

Приняв эту трактовку товара 2, удобно думать о нем как о том количестве долларов, которое потребитель может истратить на все другие товары. При подобном истолковании цена товара 2 автоматически оказывается равной 1, поскольку цена одного доллара есть доллар. Таким образом, бюджетное ограничение примет вид:

Данное выражение говорит нам просто о том, что сумма денег р₁х₁, израсходованная на товар 1, и сумма денег, израсходованная на все другие товары, х₂, взятые вместе, не должны превышать общей суммы денег m, которую может расходовать данный потребитель.

Мы говорим, что товар 2 представляет композитный товар, воплощающий в себе все то, что хотел бы потребить данный потребитель, помимо товара 1. Что касается алгебраической формы бюджетного ограничения, уравнение (2.2) есть просто особый случай формулы, заданной уравнением (2.1), при р₂ = 1, так что все то, что можно сказать о бюджетном ограничении вообще, будет верным и для трактовки товара 2 как композитного.

2.3. Свойства бюджетного множества

Бюджетная линия есть множество наборов, которые стят в точности m:

Это товарные наборы, на которые полностью расходуется весь доход потребителя.

Бюджетное множество изображено на рис.2.1. Жирной линией изображена бюджетная линия — наборы, стящие в точности m; а под этой линией располагаются наборы, которые стят строго меньше m.

Рис. 2.1

Бюджетное множество. Бюджетное множество состоит из всех наборов, доступных при данных ценах и доходе.

Можно преобразовать уравнение бюджетной линии в уравнение (2.3), что даст нам формулу

x₂ = — x₁. (2.4) Это формула для прямой, пересекающей вертикальную ось в точке m/p₂ и имеющей наклон –p₁/p₂. Данная формула показывает, сколько единиц товара 2 должен потребить потребитель, чтобы при потреблении x₁ единиц товара 1 бюджетное ограничение как раз удовлетворялось.

Приведем легкий способ нарисовать бюджетную линию при заданных ценах (p₁, p₂) и доходе m. Достаточно спросить себя, сколько товара 2 мог бы купить потребитель, если бы он истратил на него все свои деньги. Ответ: конечно, m/p₂. Теперь спросите, сколько товара 1 мог бы купить потребитель, если бы он истратил на него все свои деньги. Ответ: m/p₁. Таким образом, точки пересечения с горизонтальной и вертикальной осями показывают количества товаров, которые мог бы получить потребитель, если бы он истратил все свои деньги соответственно на товары 1 и 2. Чтобы провести данную бюджетную линию, достаточно нанести эти две точки на соответствующие оси графика и соединить их прямой линией.

Наклон бюджетной линии имеет красивую экономическую интерпретацию. Он показывает пропорцию, в которой рынок готов «заместить» товар 2 товаром 1. Предположим, например, что потребитель намерен увеличить свое потребление товара 1 на x Насколько должно измениться потребление товара 2 данным потребителем, чтобы его бюджетное ограничение удовлетворялось? Для обозначения изменения потребления товара 2 данным потребителем будем использовать x₂.

А теперь заметим, что если данное бюджетное ограничение удовлетворяется и до, и после изменений, то тем самым должны удовлетворяться равенства

. Вычитание первого уравнения из второго дает

p₁x₁ + p₂x₂= 0.

Это уравнение показывает, что общая величина изменения потребления данного потребителя должна равняться нулю. Выразив из данного уравнения x₂/x₁ — пропорцию, в которой товар 2 можно заместить товаром 1, не нарушая при этом бюджетного ограничения, получим

Это не что иное, как наклон бюджетной линии. Отрицательный знак стоит перед ним потому, что x₁ и x₂ всегда должны иметь противоположные знаки. Если вы потребляете больше товара 1, вам приходится потреблять меньше товара 2, и наоборот, чтобы заданное бюджетное ограничение по-прежнему удовлетворялось.

Иногда экономисты говорят, что наклон бюджетной линии показывает альтернативные издержки потребления товара 1. Чтобы потребить больше товара 1, приходится отказаться от некоторой величины потребления товара 2. Отказ от возможности потребления товара 2 есть истинные экономические издержки большего потребления товара 1; и эти издержки измеряются наклоном бюджетной линии.

2.4. Как изменяется бюджетная линия При изменении цен и дохода изменяется и множество товаров, доступное потребителю. Как влияют эти изменения на бюджетное множество?

Вначале рассмотрим изменения дохода. Из уравнения (2.4) нетрудно увидеть, что возрастание дохода приведет к увеличению отрезка, отсекаемого бюджетной линией на вертикальной оси, не повлияв при этом на наклон этой линии. Таким образом, рост дохода будет иметь результатом параллельный сдвиг бюджетной линии вовне, как на рис.2.2. Аналогично, уменьшение дохода вызовет параллельный сдвиг бюджетной линии внутрь.

Рис. 2.2

Возрастание дохода. Возрастание дохода вызывает параллельный сдвиг бюджетной линии наружу. А что можно сказать об изменениях цен? Вначале рассмотрим возрастание цены товара 1, считая цену товара 2 и доход постоянными. Как видно из уравнения (2.4), возрастание p₁ не изменит точки пересечения бюджетной линии с вертикальной осью, но сделает бюджетную линию круче, поскольку p₁/p₂ увеличится.

Другой способ посмотреть, как изменится бюджетная линия, состоит в том, чтобы прибегнуть к приему, описанному нами выше при проведении бюджетной линии. Если вы тратите все деньги на товар 2, то возрастание цены товара 1 не изменяет максимального количества товара 2, которое вы можете купить, следовательно, точка пересечения бюджетной линии с вертикальной осью не меняется. Но если вы тратите все деньги на товар 1 и он становится дороже, то потребление вами товара 2 должно сократиться. Следовательно, точка пересечения бюджетной линии с горизонтальной осью должна сдвинуться внутрь, в результате чего наклон бюджетной линии будет больше (рис.2.3).

Рис. 2.3

Возрастание цены. Если товар 1 становится дороже, бюджетная линия становится круче.

Что происходит с бюджетной линией при одновременном изменении цен товара 1 и товара 2? Предположим, например, что мы удваиваем цены обоих товаров. В этом случае и точка пересечения бюджетной линии с горизонтальной осью, и точка ее пересечения с вертикальной осью сдвинутся внутрь, причем координаты новых точек будут равны координатам прежних точек, умноженным на 1/2, и поэтому бюджетная линия сдвигается внутрь также с коэффициентом 1/2. Умножение обеих цен на два — то же самое, что деление дохода на 2.

Это можно выразить и алгебраически. Предположим, что наша исходная бюджетная линия есть

Предположим, далее, что обе цены возрастают в t раз. Умножение обеих цен на t дает

Но это уравнение — то же самое, что и

Таким образом, умножение обеих цен на постоянную величину t есть то же самое, что и деление дохода на эту постоянную величину t. Отсюда следует, что если умножить на t и цены обоих товаров, и доход, то бюджетная линия совсем не изменится.

Можно также рассмотреть одновременные изменения цен и дохода. Что произойдет, если цены обоих товаров возрастут, а доход снизится? Подумайте, что произойдет с точками пересечения бюджетной линии с горизонтальной и вертикальной осями. Если m уменьшается, а p₁ и p₂ растут, то соответствующие координаты обеих точек пересечения с осями m/p₁ и m/p₂ должны уменьшиться. Это означает, что бюджетная линия сдвинется внутрь. А что произойдет с наклоном бюджетной линии? Если цена товара 2 возрастет в большей степени, чем цена товара 1, так что – p₁/p₂ уменьшится (по абсолютной величине), бюджетная линия станет более пологой; если же цена товара 2 возрастет в меньшей степени, чем цена товара 1, бюджетная линия станет более крутой.

Бюджетная линия определяется двумя ценами и одним доходом, но одна из этих переменных лишняя. Мы могли бы придать одной из цен или доходу некое постоянное значение и соответствующим образом изменить другие переменные так, чтобы получить в точности то же самое бюджетное множество. Таким образом, бюджетная линия

есть в точности та же бюджетная линия, что и

x₁ + x₂ =

x₁ + x₂ = 1,

так как первая бюджетная линия получена делением всех членов уравнения на р₂, а вторая — делением всех членов уравнения на m. В первом случае мы приравняли р₂ к 1, а во втором — приравняли m к 1. Приравнивание цены одного из товаров или дохода к 1 и соответствующее изменение второй цены и дохода совершенно не изменяют бюджетного множества.

Когда мы приравниваем к 1 одну из цен, как это сделано выше, мы называем эту цену ценой-измерителем. Цена-измеритель — это цена, относительно которой мы измеряем цену другого товара и доход. Иногда бывает удобно считать один из товаров товаром-измерителем, поскольку тем самым изменение одной из цен исключается из рассмотрения.

2.6. Налоги, субсидии и рационирование

В экономической политике часто используются инструменты, оказывающие воздействие на бюджетное ограничение потребителя, скажем, налоги. Например, если правительство вводит налог на объем покупок, это означает, что потребитель должен платить правительству определенную сумму с каждой покупаемой им единицы товара. В США, например, потребители платят в виде федерального налога на бензин около 15 центов за галлон.

Как влияет налог на объем покупок на бюджетную линию потребителя? С точки зрения потребителя, налог — это то же самое, что и повышение цены. Следовательно, налог в t долларов на единицу товара 1 просто изменяет цену товара 1 с р₁ на р₁ + t. Как мы видели выше, это означает, что бюджетная линия должна стать круче.

Другой вид налога — налог на стоимость. Названием подразумевается, что им облагается стоимость — цена товара, а не купленное количество товара. Налог на стоимость обычно выражается в процентах. В большинстве штатов США действуют налоги с оборота. Если налог с оборота составляет 6%, то товар, оцениваемый в 1$, фактически продается за 1,06$. ( Налоги на стоимость называют также налогами ad valorem).

Если товар 1 имеет цену р₁, но облагается налогом с оборота по ставке , то фактически для потребителя цена равна (1 + t)р₁. Потребитель должен заплатить р₁ поставщику и tр₁ правительству за каждую единицу товара, так что общая стоимость товара для потребителя составит (1 + t)р₁.

Субсидия — противоположность налога. В случае субсидии на объем покупок правительство дает потребителю сумму, размер которой зависит от купленного количества товара. Если бы, например, потребление молока субсидировалось, правительство выплачивало бы каждому потребителю молока некоторую сумму, зависящую от количества молока, покупаемого этим потребителем. Если бы субсидия составляла s долларов на единицу потребления товара 1, то, с точки зрения потребителя, цена товара 1 равнялась бы p₁ – s. Это привело бы к тому, что бюджетная линия стала бы более пологой.

Аналогично, субсидия на стоимость (или долевая субсидия — прим. науч. ред.) есть субсидия, основанная на цене субсидируемого товара. Если правительство возвращает вам 1$ из каждых 2$, которые вы жертвуете на цели благотворительности, то ваши пожертвования на цели благотворительности субсидируются по ставке в 50%. Вообще, если цена товара 1 равна р₁ и товар 1 субсидируется в форме долевой субсидии по ставке s , то фактическая цена товара 1 для потребителя равна (1 — s)p₁.

Как видим, воздействие налогов и субсидий на цены совершенно одинаково, за исключением алгебраического знака: налог повышает цену для потребителя, а субсидия понижает ее.

Другой вид налога или субсидии, который может использоваться правительством, — аккордный налог или аккордная (недолевая) субсидия. В случае налога это означает, что правительство отбирает некую сумму денег, не зависящую от поведения индивида. Следовательно, введение аккордного налога означает, что бюджетная линия потребителя сдвинется внутрь, поскольку его денежный доход был сокращен. Аналогично, аккордная субсидия означает сдвиг бюджетной линии наружу. Налоги на объем покупок и налоги на стоимость в разной степени увеличивают крутизну бюджетной линии в зависимости от того, какой товар ими облагается, аккордный же налог всегда сдвигает бюджетную линию внутрь.

Иногда правительства вводят также нормирующие (рационирующие) ограничения. Это означает, что устанавливается некий уровень потребления какого-то товара, превышение которого запрещено. Например, во время Второй мировой войны правительство США нормировало потребление некоторых видов продуктов питания, таких, как масло и мясо.

Допустим, например, что вследствие нормирования товара 1 данный потребитель не может потреблять его в количестве большем, чем ₁. Тогда бюджетное множество для данного потребителя примет вид, изображенный на рис.2.4: оно будет представлять собой прежнее бюджетное множество, но с «отсеченным» куском. Этот «отсеченный» кусок состоит из всех наборов, которые доступны, но у которых x₁ > ₁.

Рис. 2.4

Бюджетное множество при нормировании потребления. Если потребление товара 1 нормируется, то часть бюджетного множества, выходящая за рамки количества, установленного нормированием, отсекается.

Иногда налоги, субсидии и нормирование потребления применяются совместно. Например, можно рассмотреть ситуацию, в которой потребитель мог бы потреблять товар 1 по цене до какого-то уровня , а затем должен был бы платить налог t на весь объем потребления, превышающий . Бюджетное ограничение для такого потребителя изображено на рис.2.5. Здесь наклон бюджетной линии составляет –р₁/р₂ слева от и —(р₁ + t)/р₂ справа от .

ПРИМЕР: Программа продовольственных талонов

С момента принятия Закона 1964 г. о введении продовольственных талонов федеральное правительство предоставляло субсидию на питание для бедных слоев населения. Детали этой программы несколько раз корректировались. Здесь мы опишем экономические последствия одной из этих корректировок.

Рис. 2.5

Обложение налогом потребления, превышающего. В рамках данного бюджетного множества потребитель должен платить налог лишь на потребление товара 1, превышающее величину , так что бюджетная линия справа от становится круче.

До 1979 г. домохозяйствам, соответствовавшим определенным установленным требованиям, разрешалось покупать продовольственные талоны, которые затем можно было использовать для покупки продовольствия в определенных магазинах. В январе 1975 г., например, семья из четырех человек благодаря участию в программе могла получить в форме продовольственных талонов максимальное ежемесячное пособие из бюджета в размере 153$.

Цена этих талонов для домохозяйства зависела от его дохода. Семья из четырех человек со скорректированным ежемесячным доходом в размере 300$ платила за полное месячное пособие в форме продовольственных талонов 83$. Если бы месячный доход семьи из четырех человек составлял 100$, полное месячное пособие из бюджета в форме продовольственных талонов обошлось бы ей в 25$

До 1979г. Программа продовольственных талонов представляла собой долевую субсидию на продовольствие. Ставка, по которой субсидировалось продовольствие, зависела от дохода домохозяйства. Семья из четырех человек, которой пособие обходилось в 83$, платила 1$, получая при этом продовольствия на 1,84$ (1,84 равняется 153, деленным на 83). Аналогично, домохозяйство, выплачивавшее 25$, платило 1$, получая при этом продовольствия на 6,12$ (6,12 равняется 153, деленным на 25).

Воздействие Программы продовольственных талонов на бюджетное множество домохозяйства изображено на рис.2.6A. Здесь сумма денег, затраченная на продовольствие, отложена по горизонтальной оси, а расходы на все другие товары — по вертикальной. Поскольку каждый товар измеряется в деньгах, затраченных на него, «цена» каждого товара автоматически оказывается равной 1, и бюджетная линия поэтому имеет наклон, равный —1.

Продовольственные талоны. Воздействие Программы продовольственных талонов на бюджетную линию: A — воздействие Программы до 1979г., B — после 1979 г.

Если домохозяйству разрешается купить продовольственных талонов на сумму в 153$ за 25$, это составляет субсидию на покупку продовольствия в размере примерно 84% (1 – 25/153), так что наклон бюджетной линии будет равен примерно –0,16 (25/153) до тех пор, пока домохозяйство не истратит на продовольствие 153$. Каждый доллар, затрачиваемый домохозяйством на продовольствие вплоть до суммы в 153$, сокращает потребление других товаров примерно на 16 центов. После того как домохозяйство истратит на продовольствие 153$, его бюджетная линия снова будет иметь наклон, равный —1.

Это воздействие ведет к появлению «излома», изображенного на рис.2.6. Домохозяйство с более высоким доходом должно было платить больше за свое пособие в форме продовольственных талонов. Следовательно, бюджетная линия становилась бы круче по мере роста дохода домохозяйства.

В 1979 г. в Программу продовольственных талонов были внесены изменения. Отныне вместо того, чтобы требовать от домохозяйств покупки продовольственных талонов, их просто раздают соответствующим домохозяйствам. На рис.2.6 style=’font-size:5.0pt;font-family: B показано, как это влияет на бюджетное множество.

Предположим, что домохозяйство получает субсидию продовольственными талонами на 200$ в месяц. Это означает, что теперь домохозяйство может потребить в месяц продовольствия больше на сумму в 200$ независимо от того, сколько денег оно расходует на другие товары, что подразумевает сдвиг бюджетной линии вправо на 200$. Наклон бюджетной линии не изменится: если истратить на продовольствие на 1$ меньше, можно истратить на 1$ больше на все другие товары. Но поскольку домохозяйство не может на законных основаниях продавать продовольственные талоны, максимальная сумма, которую оно может истратить на другие товары, не меняется. Программа продовольственных талонов фактически является аккордной субсидией, за исключением того обстоятельства, что продовольственные талоны не могут быть проданы.

2.7. Изменения бюджетной линии

В следующей главе мы исследуем, каким образом потребитель выбирает оптимальный потребительский набор из своего бюджетного множества. Однако уже сейчас можно сделать некоторые замечания, вытекающие из того, что мы узнали об изменениях бюджетной линии.

Во-первых, можно отметить, что поскольку при умножении всех цен и дохода на положительное число бюджетный набор не изменяется, оптимальный набор, выбираемый потребителем из бюджетного множества, также не может измениться. Еще не приступив к исследованию собственно процесса выбора, мы пришли к важному заключению: совершенно сбалансированная инфляция — та, при которой все цены и доход растут одинаковым темпом — не изменяет ничьего бюджетного множества и, следовательно, не может изменить чей-либо оптимальный выбор.

Во-вторых, можно сделать некоторые утверждения в отношении уровня благосостояния потребителя при различных ценах и доходах. Допустим, что доход потребителя растет, а все цены остаются неизменными. Нам известно, что это означает параллельный сдвиг бюджетной линии наружу. Следовательно, любой набор, потреблявшийся потребителем при более низком уровне дохода, может также быть выбран при более высоком доходе. Но тогда при более высоком доходе благосостояние потребителя должно быть по крайней мере не ниже, чем при более низком доходе, поскольку доступными объектами выбора потребителя теперь являются те же самые наборы, что и раньше, плюс какие-то еще. Аналогично если цена на один из товаров снижается, а все другие цены остаются прежними, благосостояние потребителя должно остаться по крайней мере на прежнем уровне. Это простое замечание очень пригодится нам далее.

1. Бюджетное множество состоит из всех товарных наборов, которые доступны потребителю при заданных ценах и доходе. Как правило, мы будем предполагать, что имеются только два товара, но данное предполо-жение носит более общий характер, чем кажется.

2. Уравнение бюджетной линии имеет вид p₁x₁ + p₂x₂ = m. Наклон бюджетной линии равен –p₁/p₂, точка ее пересечения с вертикальной осью задана координатой m/p₂, а точка пересечения с горизонтальной осью — координатой m/p₁.

3. Увеличение дохода вызывает сдвиг бюджетной линии наружу. Увеличение цены товара 1 делает бюджетную линию более крутой. Увеличение цены товара 2 делает бюджетную линию более пологой.

4. Налоги, субсидии и нормирование потребления вызывают изменение на-клона и положения бюджетной линии вследствие изменения цен, которые платит потребитель.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Первоначально бюджетная линия потребителя имеет вид p₁x₁ + p₂x₂ = m. Затем цена товара 1 удваивается, цена товара 2 повышается в 8 раз, а доход увеличивается в 4 раза. Запишите уравнение для новой бюджетной линии, выразив его через исходные цены и доход.

2. Что произойдет с бюджетной линией, если цена товара 2 возрастает, а цена товара 1 и доход остаются без изменений?

3. При удвоении цены товара 1 и утроении цены товара 2 станет ли бюджет-ная линия более пологой или же более крутой?

4. Приведите определение товара-измерителя.

5. Предположим, что правительство вводит налог на бензин в размере 15 центов за галлон, а затем решает ввести субсидию на бензин по ставке 7 центов за галлон. Какому чистому налогу эквивалентна указанная комби-нация?

6. Предположим, что уравнение бюджетной линии задано в виде p₁x₁ + p₂x₂ = m. Правительство решает ввести аккордный налог в размере u, налог на объем покупок товара 1 по ставке t и субсидию на объем покупок товара 2 в размере s. Как будет выглядеть уравнение новой бюджетной линии?

7. Если одновременно происходят увеличение дохода потребителя и сни-жение цены одного из товаров, то можно ли утверждать, что благосос-тояние потребителя при этом по крайней мере не снизится?

Видео:Бюджетное ограничениеСкачать

Рабочая программа (стр. 3 )

Предположим что уравнение бюджетной линии задано в виде

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

а) основная литература:

1. Иохин теория: учебник. / . — М.: изд-во РГТЭУ, 2010.

2. Курс экономической теории: учебник / Под ред. , ‑ Киров, 2007.

3. Экономическая теория: вопросы и ответы, задачи и решения: Учебное пособие. / Под ред. . — М.: Экономистъ, 2008.

4. Вэриан . Промежуточный уровень. Современный подход. – М.: ЮНИТИ, 1997. – 767 с.

5. , , Моргунов . В 2-х т. – СПб.: Экономическая школа. 2004.

6. , Фролова . Промежуточный уровень: Учебник. – М.: ИНФРА-М, 2008. – 685 с.

б) дополнительная литература:

7. Микроэкономика: практический подход (Managerial Economics) / Под ред. и . ‑ М., 2008.

8. Нуреев микроэкономики / . ‑ М.: НОРМА, 2008.

9. Нуреев, общественного выбора : учеб. пособие для вузов / ; Гос. Ун-т — Высшая школа экономики. — М.: Изд. дом ГУ ВШЭ, 2005.

10. Курс экономической теории: учебное пособие / Рук. авт. колл. . ‑ М.: ДИС, 2007

11. Экономическая теория / Под ред. . – М., 2007

12. Экономикс: принципы, проблемы и политика. В 2 томах. – пер. с англ. / – М.: ИНФА-М, 2007.

13. Экономика – 18-е изд.: пер. с англ. / – М.: Вильямс, 2007.

8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

1. Аудитории для проведения лекционных и семинарских занятий

2. Кабинет по экономической теории

9. ОЦЕНОЧНЫЕ СРЕДСТВА

9.1 Оценочные средства для входного контроля.

1. На рынке чистой конкуренции имеют место формы конкурентной борьбы:

г. лидерство в ценах

д. тайный сговор

2. Укажите, критерий определения объема производства, обеспечивающего предприятию максимум прибыли:

а. наименьший разрыв между общими и переменными издержками

в. совпадение общей выручки с общими издержками

г. наибольшая разность между валовым доходом и величиной общих издержек

д. равенство предельного дохода и предельных издержек

3. Для долгосрочного равновесия предприятия-конкурента характерно все перечисленное ниже, кроме:

а. средних общих издержек, превышающих цену

б. цены, равной минимальным средним общим издержкам

в. цены, равной предельным издержкам

г. предельных издержек, равных минимальным средним общим издержкам

д. цены, которая ниже минимальных средних общих издержек

4. На рисунке представлена графическая модель доходов и издержек конкурентного предприятия

Каков объем производства (Q), при котором фирма минимизирует убытки:

5.Фирма планирует выпустить учебник “Экономическая теория”. Средние издержки на производство книги составляют 100 + 100000/Q, где Q – количество учебников, выпущенных за год. Планируемая цена книги 200 руб. Каков должен быть годовой тираж учебника, соответствующий точке безубыточности?

6.Зависимость общих издержек предприятия (ТС) рублей от объема производства (Q) штук в день представлена таблицей:

При какой цене товара предприятие прекратит его производство в долгосрочном периоде?

7.Функция общих издержек фирмы задана формулой ТС = 8q + 8q2. Осуществляя производство 20 единиц товара и реализуя их на совершенно конкурентном рынке по цене 126 руб. за единицу, фирма получит

а. прибыль 2040 руб.

б. убытки 2040 руб.

в. недостаточно данных

1. В условиях чистой монополии предприятие:

а. соглашается с ценой равновесия конкурентного рынка

б. частично контролирует цены

в. лидирует в ценовой политике

г. полностью контролирует цены

д. может проводить политику ценовой дискриминации

2. Монополист отличается от чисто конкурентного предприятия тем, что может:

а. сокращать издержки производства

б. максимизировать прибыль при равенстве предельного дохода и предельных издержек

г. выбирать комбинацию цены и объема выпуска, которая обеспечивает получение максимальной прибыли

д. может устанавливать более высокую цену

3. Монополист, реализуя свой продукт по разным ценам различным группам потребителей, осуществляет:

а. ценовое регулирование

б. ценовую дискриминацию

в. ценовую экспансию

д. политику выравнивания цен

4. На рисунке представлена графическая модель доходов и издержек фирмы-монополиста.

Объем производства (Q), при котором фирма монополист максимизирует прибыль, равна:

Тема. Предприятие в условиях монополистической конкуренции и олигополии.

1. Долгосрочная равновесная цена в условиях монополистической конкуренции:

а. выше средних переменных издержек

б. ниже минимальных средних общих издержек

в. равна средним переменным издержкам

г. равна средним общим издержкам

д. ниже средних общих издержек

2. Неценовая конкуренция включает в себя:

а. дифференциацию продукта

б. совершенствование продукта

г. увеличение продаж от понижения цены

д. увеличение прибыли благодаря повышению цен

3. Тайный или молчаливый сговор между предприятиями невозможен, если:

а. существуют невысокие барьеры вступления в отрасль новых предприятий

б. налицо процесс централизации капитала

в. число предприятий возрастает

г. относительно высокая конкуренция

д. имеется малое число предприятий и непреодолимые барьеры вступления в отрасль

4. Предприятия, пошедшие на тайный сговор, ведут себя как:

а. чистый монополист

б. совершенный конкурент

в. конкурирующий монополист

г. доминирующее предприятие

д. следующие за лидером предприятия

5. Проанализировав график, посчитайте максимальную прибыль предприятия работающего на рыке монополистической конкуренции.

Тема. Спрос на ресурсы и их эффективное использование.

1. Спрос на ресурсы зависит от:

б. предложения товара, в изготовлении которого используется ресурс

в. спроса на товар, в изготовлении которого используется этот ресурс

г. запасов ресурса

д. цен на взаимозаменяемые товары

2. Прирост издержек, вызванный использованием каждой дополнительной единицы привлекаемого ресурса, называется:

а. предельными издержками на продукт

б. предельными издержками на ресурс

г. средними издержками на ресурс

д. предельными затратами на ресурс

3. Для предприятия будет выгодным применять дополнительные единицы ресурса до тех пор, пока:

а. предельный доход не станет равным предельным издержкам продукта

б. предельная доходность ресурса не станет равной предельным издержкам на него

в. предельный продукт больше предельных издержек продукта

г. стоимость предельного продукта ниже цены ресурса

д. предельная доходность ресурса больше его предельных издержек

4.Производственная функция имеет вид Y=K∙L. Если общий объем затрат не должен превышать 30, цена труда равна 4, цена капитала — 5, то при какой комбинации труда и капитала будет достигнут максимальный выпуск?

5. Производственная функция фирмы имеет вид Y=100K∙L. Цена труда составляет 30, а капитала — 120. Чему равны средние издержки производства 100 единиц продукции, если фирма выбирает самый дешевый способ производства?

6.Совершенно конкурентное предприятие использует ресурсы X и Y, покупая их также на совершенно конкурентном рынке по ценам: Цх=120 руб., Цу=90 руб. Если предельный продукт ресурса Х равен 20 ед., а ресурса Y — 15 ед., то при какой цене на товар предприятие будет максимизировать прибыль?

Ответы на тесты

Предприятие в условиях чистой конкуренции.

Предприятие в условиях чистой монополии.

Предприятие в условиях монополистической конкуренции и олигополии

Спрос на ресурсы и их эффективное использование

9.2 Оценочные средства и тесты для текущего контроля успеваемости

Вопросы и задания

Ответы и решения

Предположим, что имеется 25 человек с резервной ценой в 500$ , а для 26-го человека резервная цена составляет 200$. Как выглядит кривая спроса?

Кривая спроса будет горизонтальной при резервной цене в 500 долл. для 25 квартир, а затем упадет до уровня резервной цены в 200 долл.

Какова была бы равновесная цена в вышеприведенном примере, если бы к сдаче предлагалось 24 квартиры? Что, если бы сдавалось 26 квартир? Что, если бы сдавалось 25 квартир?

В первом случае равновесная цена будет равна 500 долл., а во втором — 200 долл. В третьем случае равновесной будет любая цена, заключенная в интервале между 200 и 500 долл.

Если резервные цены у людей различны, то почему кривая рыночного спроса нисходяща?

Потому что, если мы хотим сдать еще одну квартиру, нам придется предложить более низкую цену. По мере снижения p число людей, у которых резервные цены выше p, всегда должно увеличиваться.

В тексте мы предположили, что покупатели кондоминиумов принадлежат к числу жителей внутреннего кольца — т. е., лиц, которые уже снимают квартиры. Что произошло бы с ценой квартир внутреннего кольца, если бы все покупатели кондоминиумов были жителями внешнего кольца — людьми, которые в настоящий момент не снимают квартиры во внутреннем кольце?

Цена квартир внутреннего кольца возросла бы, поскольку спрос на квартиры не изменился бы, а предложение уменьшилось.

Теперь предположим, что все покупатели кондоминиумов — люди из внутреннего кольца, но что каждый кондоминиум был построен из двух квартир. Что произошло бы в этом случае с ценой квартир?

Цена квартир внутреннего кольца возросла бы.

Как вы думаете, каковы были бы последствия введения налога на число квартир, которые будут построены в длительном периоде?

В длительном периоде налог, несомненно, привел бы к уменьшению числа квартир, предлагаемых к сдаче.

Допустим, что кривая спроса имеет вид D(p)=100 – 2p=40. Какую цену установил бы монополист, если бы у него имелось 60 квартир для сдачи? Сколько квартир он бы сдал? Какую цену он бы установил, если бы имел 40 квартир? Сколько квартир он бы сдал?

Он установил бы цену в 25 долл. и сдал бы 60 квартир. Во втором случае он сдал бы все 40 квартир по максимальной цене, приемлемой рынком. Эту цену мы находим из уравнения D(p) = 100 — 2p = 40, решение которого есть p* = 30.

Если бы рассматриваемая нами модель контроля за арендной платой допускала неограниченную передачу в субаренду, то кто в итоге получил бы квартиры во внутреннем кольце? Был бы такой исход эффективным по Парето или нет?

Все, у кого резервная цена выше равновесной цены конкурентного рынка, так что конечный исход был бы эффективным по Парето. (Разумеется, в длительном периоде, возможно было бы построено меньше новых квартир, что привело бы к неэффективности другого рода.)

Первоначально бюджетная линия потребителя имеет вид p1x1 + p2x2 = m. Затем цена товара 1 удваивается, цена товара 2 повышается в 8 раз, а доход увеличивается в 4 раза. Запишите уравнение для новой бюджетной линии, выразив его через исходные цены и доход.

Новая бюджетная линия задана уравнением 2p1x1 + 8p2x2 = 4m.

Что произойдет с бюджетной линией, если цена товара 2 возрастает, а цена товара 1 и доход остаются без изменений?

Точка пересечения с вертикальной осью (осью x2) опускается ниже, а точка пересечения с горизонтальной осью (осью x1) остается той же самой. Поэтому бюджетная линия становится более пологой.

При удвоении цены товара 1 и утроении цены товара 2 станет ли бюджетная линия более пологой или же более крутой?

Более пологой. Ее наклон есть —2p1/3p2.

Приведите определение товара-измерителя.

Товар, цена которого была приравнена к 1; цены всех других товаров измеряются относительно цены товара-измерителя.

Предположим, что правительство вводит налог на бензин в размере 15 центов за галлон, а затем решает ввести субсидию на бензин по ставке 7 центов за галлон. Какому чистому налогу эквивалентна указанная комбинация?

Налогу в размере 8 центов за галлон.

Предположим, что уравнение бюджетной линии задано в виде p1x1 + p2x2 = m. Правительство решает ввести аккордный налог в размере u, налог на объем покупок товара 1 по ставке t и субсидию на объем покупок товара 2 в размере s. Как будет выглядеть уравнение новой бюджетной линии?

Если одновременно происходят увеличение дохода потребителя и сни-жение цены одного из товаров, то можно ли утверждать, что благосос-тояние потребителя при этом по крайней мере не снизится?

Да, поскольку все наборы, которые были доступны потребителю ранее, доступны ему при новых ценах и доходе.

Если мы видим, что потребитель выбирает набор (x1, x2), при том, что одновременно ему доступен набор (y1, y2), можем ли мы заключить, что (x1, x2) f (y1, y2)?

Нет. Потребителю могло бы быть и безразлично, какой из двух наборов выбрать. Единственное, что мы можем заключить с полным основанием, это то, что (x1, x2) (y1, y2).

Рассмотрите для группы людей A, B,C отношение «по меньшей мере такой же высокий, как», например, как в утверждении «A по меньшей мере такой же высокий, как и B». Является ли это отношение транзитивным? Характеризуется ли оно полной упорядоченностью (сравнимостью)?

На оба вопроса следует ответить «да».

Рассмотрите отношение «строго выше, чем» для той же группы людей. Транзитивно ли это отношение? Рефлексивно ли оно? Характеризуется ли оно полной упорядоченностью?

Это отношение предпочтения транзитивно, но не характеризуется полной упорядоченностью — оба человека могли бы быть одного роста. Оно не рефлексивно, так как неверным является утверждение, что человек строго выше себя самого.

Тренер колледжа по футболу заявляет, что из двух судей на линии — A и B — он всегда предпочитает того, который крупнее по комплекции и быстрее бегает. Является ли данное отношение предпочтения транзи-тивным? Характеризуется ли оно полной упорядоченностью?

Это отношение предпочтения транзитивно, но не характеризуется полной упорядоченностью. Что, если бы A был крупнее B, но двигался бы медленнее? Кого из двоих предпочел бы тренер?

Если и стручковый перец, и анчоусы — антиблага, то каким будет наклон кривой безразличия — положительным или отрицательным?

Отрицательный наклон. Если вы дадите потребителю больше анчоусов, вы тем самым понизите его благосостояние, поэтому придется забрать у него немного стручкового перца, чтобы вернуть его на его кривую безразличия. В этом случае полезность возрастает в направлении к началу координат.

Объясните, почему выпуклые предпочтения означают, что «средние наборы предпочитаются крайним».

Потому что потребитель слабо предпочитает взвешенное среднее двух наборов третьему.

Какова ваша предельная норма замещения 1-долларовых купюр 5-долларовыми?

Если вы откажетесь от одной 5-долларовой купюры, то сколько 1-долларовых купюр вам потребуется в качестве компенсации? Вполне достаточно будет пяти купюр по 1 доллару. Следовательно, ответ составит —5 или —1/5 в зависимости от того, какой из товаров вы откладываете на горизонтальной оси.

Если товар 1 — «безразличное благо», то какова предельная норма его замещения товаром 2?

Ноль — если вы заберете у потребителя немного товара 1, то ему потребуется ноль единиц товара 2, чтобы компенсировать эту потерю.

Какова функция спроса на товар 2 в случае, если два товара являются совершенными субститутами?

Анчоусы и арахисовое масло, шотландское виски и напиток «Кул Эйд» и другие подобные им омерзительные сочетания.

Предположим, что кривые безразличия представляют собой прямые линии с наклоном, равным —b. Как будет выглядеть оптимальный выбор потребителя при заданных произвольных ценах p1, p2 и денежном доходе m?

x2 = 0 при p2 > p1, x2 = m/p2 при p2 b, и любое количество товаров, лежащее на бюджетной линии, если p1/p2 = b .

Предположим, что ваши предпочтения в отношении мороженого и оливок описываются вогнутыми кривыми безразличия, подобными приведенным в тексте настоящей главы, и что вы можете потратить на эти товары m долларов, а их цены составляют соответственно p149 и p250. Перечислите варианты выбора оптимальных потребительских наборов.

Пусть z — число чашек кофе, покупаемых потребителем. Тогда нам известно, что 2z есть число покупаемых им чайных ложек сахара. Должно удовлетворяться бюджетное ограничение 2 p1z + p2z = m. Выразив из этого уравнения z, мы получаем z = . Нам известно, что вы потребляете либо сразу все мороженое, либо сразу все оливки. Поэтому двумя оптимальными потребительскими наборами для вас будут либо x1 = = m/p1, x2 = 0, либо x1 = 0, x2 = m/p2.

При какого рода предпочтениях благосостояние потребителя будет оди-наковым как в случае налога на объем покупок, так и в случае подоходного налога?

При ломаных предпочтениях, таких, как совершенные комплементы, когда изменение цены не вызывает никакого изменения спроса.

Предположим, что в следующем периоде актив A может быть продан за 11 долл. Какова должна быть текущая цена актива A, если сходные с A активы приносят норму дохода в 10 процентов?

Актив A должен продаваться за 11/(1 + 0,10) = 10$.

Дом, который вы могли бы снять задолл. в год и продать через год за долл., можно приобрести за долл. Какова норма дохода на этот дом?

Норма дохода равна (10.000 + 10.000)/100.000 = 20%.

Нам известно, что норма дохода по необлагаемым налогом облигациям r должна быть такой, чтобы (1 — t)rt = r, следовательно, (1 — 0,40)0,10 = 0,06 = r.

Допустим, что запасы некоего редкого ресурса, спрос на который постоянен, истощатся через 10 лет. Какой должна быть цена этого редкого ресурса сегодня, если альтернативный ресурс станет доступным по цене в 40 долл. и если ставка процента составляет 10%?

Сегодняшняя цена редкого ресурса должна составлять .

Не расположенному к риску индивиду предлагается выбор между игрой, приносящей 1000 долл. с вероятностью 25% и 100 долл. с вероятностью 75%, и единовременной выплатой в 325 долл. Что он выберет?

Поскольку данный индивид не расположен к риску, он предпочитает самой игре ее ожидаемое значение 325 долл. и поэтому выберет платеж.

Что, если бы единовременная выплата составила 320 долл.?

Если платеж составит 320 долл., решение будет зависеть от вида функции полезности; мы не можем сказать ничего в общем.

Нарисуйте функцию полезности, показывающую поведение, характеризующееся расположенностью к риску при играх с малыми ставками и нерасположенностью к риску при играх с крупными ставками.

Вы должны нарисовать функцию, которая вначале является выпуклой, а затем становится вогнутой.

Почему группе домовладельцев, проживающих по соседству. может оказаться труднее осуществить взаимное страхование против наводнения, нежели против пожара?

Чтобы осуществить взаимное страхование, риски должны быть независимыми. Однако в случае ущерба от наводнения это не так. Если один из домов в данном районе терпит ущерб от наводнения, то весьма вероятно, что пострадают все дома.

Может ли существовать такое распределение, эффективное по Парето, при котором чье-либо благосостояние ниже, чем при распределении, не эффективном по Парето?

Да. Рассмотрим, например, распределение, при котором все богатство сосредоточено у одного индивида. При таком распределении благосостояние другого индивида ниже, чем при распределении, согласно которому он владеет чем-то.

Может ли существовать такое распределение, эффективное по Парето, при котором благосостояние всех индивидов ниже, чем при каком-то распределении, не являющемся эффективным по Парето?

Нет. Ведь это означало бы, что при распределении, которое, как утверждается, является эффективным по Парето, существует какой-то способ повысить благосостояние всех, что противоречит предположению об эффективности по Парето.

Верно или неверно? Если нам известна контрактная кривая, то известен исход любой сделки.

Если нам известна контрактная кривая, то любой обмен должен закончиться в какой-то точке на этой кривой; однако, где именно, мы не знаем.

Можно ли повысить благосостояние какого-то индивида, если мы находимся в точке распределения, эффективного по Парето?

Да, но при этом благосостояние кого-то другого должно понизиться.

Если на восьми из десяти рынков стоимость избыточного спроса равна нулю, то что можно сказать про два оставшихся рынка?

Сумма величин избыточного спроса на двух оставшихся рынках должна равняться нулю.

Предположим, мы говорим, что распределение x общественно предпочитается распределению y только в том случае, если каждый предпочитает распределение x распределению y. (Иногда это называют ранжи-рованием по Парето, так как данное ранжирование тесно связано с идеей эффективности по Парето.) Каков недостаток данного подхода, если пользоваться им как правилом принятия общественных решений?

Главный его недостаток состоит в том, что имеется много распределений, которые невозможно сравнить между собой — не существует способа выбрать лучшее из двух любых распределений, эффективных по Парето.

Роулсианская функция благосостояния учитывает только благосостояние того индивида, у которого оно ниже всех. Функцию, являющуюся проти-воположностью роулсианской, можно было бы назвать «ницшеанской» функцией благосостояния — функцией благосостояния, согласно которой ценность распределения зависит лишь от благосостояния индивида с наивысшим уровнем благосостояния. Каков мог быть математический вид ницшеанской функции благосостояния?

Предположим, что множество возможных полезностей — выпуклое и что потребителей заботит только собственное потребление. Какого рода рас-пределения представляют точки максимума благосостояния для ниц-шеанской функции благосостояния?

Поскольку согласно ницшеанской функции благосостояния интерес представляет лишь благосостояние того индивида, у которого оно наивысшее, максимум благосостояния при таком распределении обычно подразумевает получение всего богатства одним индивидом.

Допустим, что распределение является эффективным по Парето и что каждого индивида заботит только его собственное потребление. Докажите, что должен существовать индивид, который никому не завидует в смысле, описанном в тексте данной главы. (Над этой головоломкой придется поразмыслить, но она того стоит.)

Предположим, что это не так. Тогда каждый индивид завидует кому-то другому. Составим список индивидов с указанием того, кто кому завидует. Индивид A завидует кому-то — назовем этого человека индивидом B. Индивид B, в свою очередь, кому-то завидует, скажем, индивиду C. И т. д. В конце концов, мы найдем того, кто завидует индивиду, стоящему в списке раньше. Допустим, что мы получаем цикл «C завидует D завидует E завидует C». Теперь рассмотрим следующий обмен: C получает то, что имеется у D, D получает то, что имеется у E, а E получает то, что имеется у C. Каждый индивид, участвующий в данном цикле, получает тот набор, который он предпочитает, и поэтому благосостояние каждого из этих индивидов повышается. Но тогда первоначальное распределение не могло быть эффективным по Парето!

Рассмотрим аукцион, в ходе которого люди по очереди предлагают цену, причем каждая последующая предлагаемая цена должна быть хотя бы на доллар выше предыдущей и предмет продается тому индивиду, который предлагает за него наивысшую цену. Если ценность продаваемого товара для i-го индивида есть vi, то какова будет цена, предложенная побе-дителем? Которому из индивидов достанется товар?

Продажная цена товара не будет самой высокой из предложенных. Скорее, это будет вторая по высоте цена плюс доллар. Товар получает индивид, который готов предложить наивысшую цену, но он должен заплатить только цену, предложенную тем индивидом, который готов был заплатить вторую по высоте цену, плюс какая-то небольшая сумма.

Представим закрытые торги между n индивидами по поводу того же самого товара. Пусть vi есть ценность данного товара для индивида i. Докажите, что если данный товар продается индивиду, предлагающему вторую наивысшую цену, то в интересах каждого игрока будет сказать правду о своей оценке товара.

Аргументация аналогична той, которая была приведена в случае налога Кларка. Представьте, что вы завышаете предложенную вами цену по сравнению с вашей истинной оценкой товара. Если вы все равно являетесь лицом, предлагающим наивысшую цену, то ваши шансы на получение товара не меняются. Если вы не являетесь таким лицом, то при повышении предлагаемой вами цены, позволяющем превысить нынешнюю наивысшую предлагаемую цену, вы получите товар, но вам придется заплатить за него вторую по высоте цену из предлагаемых — а это больше суммы, в которую вы оцениваете товар. Аналогичные рассуждения можно провести и для случая занижения предложенной цены по сравнению с истинной оценкой товара.

Предположим, что 10 человек живет на одной улице и что каждый из них готов заплатить за каждый дополнительный уличный фонарь 2 долл. независимо от того, сколько этих фонарей установлено. Какое эффективное по Парето число уличных фонарей следует установить, если издержки установки x уличных фонарей заданы выражением c(x) = x2?

Мы хотим, чтобы сумма предельных норм замещения равнялась предельным издержкам предоставления общественного блага. Сумма MRS есть 20(= 10 ´ 2), а предельные издержки составляют 2x. Поэтому мы получаем уравнение 2x = 20, означающее, что x = 10. Итак, число уличных фонарей, эффективное по Парето, составляет 10.

1. Микроэкономика как наука.

3. Методы экономической науки. Специфика микроэкономического исследования.

4. Совершенная конкуренция и экономическая эффективность. Прикладные аспекты анализа конкурентных рынков.

5. Сравнительно-статический анализ долгосрочного равновесия конкурентной отрасли: сдвиги кривой спроса и сдвиги кривой долгосрочного предложения отрасли.

6. Монополия и монополистическое поведение. Особенности выбора монополиста, максимизирующего прибыль, в коротком и длительном периодах. Монопольная власть и ее измерение.

7. Естественная монополия и субаддитивность издержек. Дилемма регулирования естественной монополии. Альтернативы регулированию естественной монополии.

8. Условия и цели ценовой дискриминации. Виды ценовой дискриминации: первой, второй и третьей степени. Ценообразование по схеме двойного тарифа. Продажа товаров наборами и связанные продажи.

9. Классификация моделей монополистической конкуренции. Особенности долгосрочного равновесия фирм и отрасли в традиционных моделях монополистической конкуренции.

10. Модель пространственной дифференциации продукта Хотеллинга. Модель города на окружности (Салопа). Особенности долгосрочного равновесия фирм и отрасли в адресных моделях монополистической конкуренции.

11. Монополистическая конкуренция и эффективность.

12. Подходы к классификации моделей олигополии. Предположительные вариации как основа моделей олигополии.

13. Олигополия с закрытым входом, ориентированная на выпуск как стратегическую переменную. Модели Курно, Стэкльберга.

14. Олигополия, ориентированная на цену как стратегическую переменную: модель Бертрана (с закрытым входом) и лидерства в ценах (с закрытым и с открытым входом).

15. Модель лимитирующего выпуска. Стимул к вхождению и условие невхождения. Олигополия с открытым входом: Курно, Бертрана, сговор (картель). Развитие модели лимитирующего выпуска. Ценовая олигополия с дифференцированным продуктом.

16. Модели однократного и повторяющегося взаимодействия: картель как повторяющаяся игра. Стратегия наказания.

17. Задача максимизации прибыли фирмы в долговременном и краткосрочном промежутках. Локальное рыночное равновесие фирмы в долговременном и краткосрочном промежутках и его геометрическая интерпретация.

18. Функции спроса на ресурсы со стороны фирмы и функция предложения фирмы, их свойства.

19. Задача максимизации выпуска фирмы при лимите на ресурсы в случае долговременного промежутка и ее решение методом Лагранжа.

20. Функции условного спроса на ресурсы по Маршаллу (по Вальрасу) со стороны фирмы и функция условного предложения фирмы.

21. Задача минимизации издержек фирмы при фиксированном выпуске в случае долговременного промежутка и ее решение методом Лагранжа..

22. Функции условного спроса на ресурсы по Хиксу со стороны фирмы и функция условных издержек фирмы, их свойства.

23. Предельные издержки по выпуску и предельные издержки по цене ресурса (лемма Шепарда).

24. Локальное рыночное равновесие фирмы и линия ее развития, выпуск и издержки.

25. Экономические риски и неопределенность: понятие, сущность..

26. Функция полезности фон-Нейман — Моргенштерна и типы отношения к риску.

27. Карта кривых безразличия, предельная норма замещения и бюджетное ограничение при выборе в пространстве обусловленных благ.

28. Методы измерения риска. Плата за риск. Методы снижения рисков.

29. Информация и её свойства. Ценность и цена информации.

30. Асимметрия информации: понятие и причины, проявление на рынке труда, страховых услуг и кредитов, в отношениях между собственниками и акционерами.

31. Институты как основа формирования условий предпочтений экономических агентов.

32. Эволюция институционализма, концепция раннего институционализма. (Т. Веблен, Дж. Р. Коммонс, , Дж. К. Гэлбрейт).

33. Неоинституционализм: основные идеи, особенности и структура новой институциональной теории, экономика права, концепция Р. Коуза, теория экономических организаций.

34. Существование и стабильность общего равновесия. Типы рыночных взаимодействий.

35. Модель конкурентного рыночного равновесия Л. Вальраса. Закон Вальраса.

36. Условия достижения общего равновесия. Предпосылки достижения общего равновесия, предельная норма трансформации.

37. Эффективность по Парето. Критерий эффективности.

38. Эффективность в потреблении. Условия и механизм достижения Парето-эффективности в потреблении (обмене). Эффективность в производстве.

39. Теоремы экономической теории благосостояния.

40. Факторы, препятствующие достижению Парето-эффективности: налогообложение, монополизация рынка.

Видео:38 Задача потребителя и бюджетная линия в ящике ЭджвортаСкачать

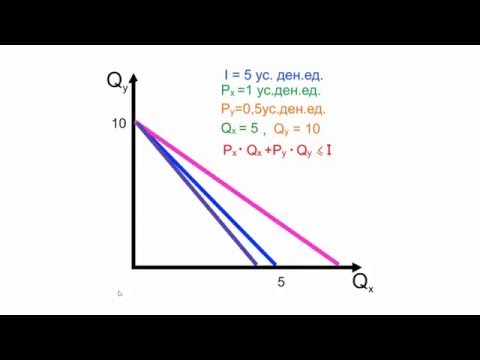
Бюджетная линия: понятие, уравнение, пример и график

Бюджетная линия (также известная как бюджетное ограничение или бюджетная строка) — это таблица или график, которые показывают ряд различных комбинаций двух продуктов, которые могут быть потреблены при заданном доходе и ценах.

Бюджетная линия для потребителей — это то же самое, что кривая производственных возможностей для производителей. Это полезный инструмент для понимания потребительского поведения и выбора.

Бюджетная линия отображает потребительский выбор между двумя продуктами. Количество единиц одного продукта отображается по горизонтальной оси, а количество единиц другого — по вертикальной.

Каждая возможная комбинация этих двух продуктов затем строится для получения кривой бюджетных ограничений.

Бюджетная линия является ограничением в том смысле, что она ограничивает общее потенциальное потребление потребителя.

Достижимо только такое сочетание двух товаров, которое укладывается в бюджетное ограничение или входит в него. Любая комбинация двух товаров, выходящая за рамки бюджетной строки, недостижима.

Вместе с кривыми безразличия потребителя, показывающими различные комбинации двух продуктов, которые дают потребителю одну и ту же полезность, можно прийти к комбинации двух товаров, которая будет оптимальной для потребителя с точки зрения максимального удовлетворения его пожеланий.

Видео:Кривые безразличия и предельная норма замещенияСкачать

Уравнение бюджетного ограничения

Совокупные расходы на любую комбинацию товаров по бюджетной статье равны доходам потребителей. Это можно выразить математически следующим образом:

где Q_A и Q_B — единицы товара A и товара B, P_A и P_B — их соответствующие цены, а I — общий доход потребителя.

Предположим, что продукт А находится на оси Y, а продукт В — на оси X. Мы можем записать бюджетное ограничение в стандартном формате прямолинейного уравнения:

Оно показывает, что наклон бюджетной линии равен отрицательному отношению цены товара по оси X к цене товара по оси Y.

Бюджетная линия смещается, когда изменяется доход потребителя: она смещается внутрь, когда доход уменьшается, и смещается наружу, когда доход увеличивается. Но когда происходит изменение цены только одного товара, бюджетная строка вращается, то есть смещается, но не параллельно.

Видео:Как спрос и предложение задают ценыСкачать

Пример

Предположим, вы получили подарочную карту AppStore на 50 долларов от своего друга. Вы подумываете о покупке видеоигр и песен для своего смартфона. Цена игры — 5 долларов, а песни — 1 доллар.

Вы можете либо потратить всю сумму на игры, и в этом случае купленные игры будут стоить 10 [= $50 / 5]. Или вы можете потратить всю сумму на музыку, и в этом случае количество купленных песен составит 50.

Скажем, количество песен представлено вдоль горизонтальной оси X, а количество игр — вдоль вертикальной оси Y. Теперь у нас есть две точки на бюджетной линии (0,10) и (50,0).

Вышеперечисленные комбинации редко приобретаются типичным потребителем. Вы, скорее всего, купите и игры, и песни в некотором количестве выше нуля.

Допустим, вы покупаете 6 игр. Это будет 30 долларов [= 4 × 5]. На оставшуюся сумму можно купить 20 песен. Теперь у нас есть еще одна точка на графике (20,6).

Если мы построим вышеприведенные точки и любые другие возможные комбинации, которые вы можете выбрать, мы получим прямую бюджетную линию, как показано ниже:

Достижимая комбинация — это любая комбинация двух продуктов, которые могут быть приобретены с использованием данного дохода. Все пункты на или ниже бюджетной линии достижимы, например, 20 песен и 4 игры.

Недостижимая комбинация — это любая комбинация двух продуктов, которую невозможно приобрести с использованием данного дохода. Все пункты выше бюджетной линии недостижимы, например, 30 песен и 6 игр.