Содержание

Примеры решений задач: функция полезности
Функция полезности: задачи с решениями
Общая полезность
Условия равновесия потребителя
Кривая безразличия
Бюджетная линия
Предельная полезность
Определение
Формула
График
Закон убывающей предельной полезности
Ограничения закона
Примеры решения задач
Задача 1
Решение
Задача 2
Решение
📸 Видео

Видео:Предельная полезностьСкачать

Примеры решений задач: функция полезности

В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.

Видео:Как мыслит потребитель? Кривые безразличияСкачать

Функция полезности: задачи с решениями

Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.

Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.

Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб. Функции общей полезности разных благ: $F(TU(x))=3sqrt$, $F(TU(y))=5sqrt$, $F(TU(z))=5sqrt$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%

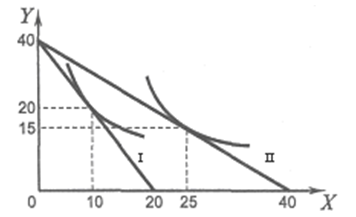
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.

Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.

Задача 5. Общая полезность благ $alpha$ и $beta$ для некоего потребителя описывается уравнениями $U_alpha = q_alpha(15 — 0,5q_alpha)$, $U_beta = q_beta(30 — q_beta)$. Допустим, потребитель располагает бюджетом для покупки $alpha$ и $beta$ в размере 120 руб., цены на $alpha$ и $beta$ равны соответственно 5 и 10 руб. Определить количество $alpha$ и $beta$, максимизирующее полезность потребителя.

Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?

Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.

Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.

Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?

Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^x_2^$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.

Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^(x_2-40)^$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^x_2^$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.

Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=sqrt$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.

Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.

Общая полезность

Предельная полезность — это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.

Производная по количеству Q Mu = dTu/dQ Как найти производную.

Например, TU = x*y. Mu_x = d(x*y)/dx = y; Mu_y = d(x*y)/dy = x
Например, TU = 10x 2 + 2x + 2. Mu_x = d(10x 2 + 2x + 2)/dx = 20x + 2

Функция полезности — функция, показывающая убывание полезности блага с ростом его количества: Tu = f(Q_i)

Видео:Закон убывающей предельной полезности #ShortsСкачать

Условия равновесия потребителя

Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.

Видео:Экономическая теория. Потребительский выбор, теория полезностиСкачать

Кривая безразличия

Предельная норма замещения (marginal rate of substitution — MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу: MRS xy = ΔY / ΔX ΔY = Y₁ — Y₀ ΔX = X₁ — X₀ или MRS xy = Mu x / Mu y

Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.

Видео:Кривые безразличия и предельная норма замещенияСкачать

Бюджетная линия

Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны P_x=2 руб. и P_y=4 руб. Найдите равновесный набор.
Решение: Из условия равновесия потребителя: Mu_x / Mu_y = P_x / P_y получаем: Mu_x = d(x*y)/dx = y; Mu_y = d(x*y)/dy = x
Тогда: y / x = 2 / 4 = 1 /₂ или y = 1 /₂x
Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4* 1 /₂x = 4x
Откуда: x = 20 ед., y = 1 /₂*20 = 10 ед.
Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.

Видео:16 Функция полезности и предельная норма замещения Существование функции полезностиСкачать

Предельная полезность

Видео:Эластичность спроса и предложения | Как цена влияет на спросСкачать

Определение

Предельная полезность (англ. Marginal Utility, MU) – это дополнительное количество полезности, которое получает потребитель от потребления следующей единицы блага. При этом кардиналисты предлагают использовать ютиль в качестве условной единицы измерения полезности.

Видео:15 Функция полезности определениеСкачать

Формула

Если общая полезность (англ. Total Utility, TU) блага задана в виде функции от его количества q, то функция предельной полезности будет ее первой производной. В общем виде она может быть записана следующим образом:

MU(q) =	δTU(q)
	δq

Поскольку функция общей полезности TU(q) достигает своего максимума при MU(q) = 0, то количество блага, при котором потребитель максимизирует полезность можно рассчитать решив следующее уравнение:

0 =	δTU(q)
	δq

Если общая полезность блага задана в виде числового ряда, то предельную полезность от потребления его n-ой единицы можно рассчитать по следующей формуле:

где TU_n – это общая полезность от потребления n единиц блага, а TU_n-1 – это общая полезность от потребления (n-1) единиц блага.

Видео:Потребление, полезность и равновесие потребителя на рынкеСкачать

График

Чтобы лучше разобраться с функцией общей и предельной полезности, рассмотрим следующий пример. Предположим, что кривая общей полезности блага описывается функцией:

График этой функции представлен на рисунке ниже.

Функция предельной полезности будет первой производной от функции общей полезности, а именно:

Ее график приведен на рисунке ниже.

Следует отметить, что предельная полезность равна нулю в тот момент, когда потребитель полностью удовлетворил свою потребность в данном благе. В этот же самый момент общая полезность достигает своего максимума. Дальнейшее потребление данного блага будет обладать отрицательной предельной полезностью, поэтому рациональный потребитель прекратит потребление.

Чтобы найти максимум функции общей полезности для условия данного примера, необходимо решить следующее уравнение:

Таким образом, потребитель максимизирует свою полезность потребив 23,3 единицы блага.

Видео:ИнЭИ Экономика Лекция №1.1 «Теория потребительского поведения»Скачать

Закон убывающей предельной полезности

Закон убывающей предельной полезности утверждает, что полезность каждой следующей потребленной единицы блага снижается по сравнению с предыдущей единицей. При этом общая полезность увеличивается до того момента, пока предельная полезность не станет равна нулю.

Ограничения закона

Следует отметить, что действие этого закона возможно при выполнении следующих ограничений.

Потребитель принимает решение рационально.
Цена одной единицы блага неизменна. Цена является важным фактором, который принимает во внимание рациональный потребитель при принятии того или иного решения. Поскольку потребление одного блага осуществляется за счет отказа от потребления других благ, изменение цены может повлиять на пересмотр полезности этих благ для потребителя. В этом случае закон убывания предельной полезности может перестать выполняться, поэтому неизменность цен является обязательным условием.
Потребляемое благо однородно. Другими словами, каждая следующая единица потребляемого блага должна быть полностью идентична предыдущей.
Потребление блага осуществляется непрерывно. Каждая следующая единица блага потребляется непосредственно сразу за предыдущей. Если возникает перерывы в потреблении предельная полезность блага может не уменьшаться.

Принимая решение рациональный потребитель действует следующим образом:

максимизирует полезность;
предпочитает получить как можно больше благ;
имеет возможность сравнивать различные альтернативы (имеет доступ к необходимой информации);
остается последовательным в своих предпочтениях.

Видео:5.1 Предельные издержки и маржинальный анализСкачать

Примеры решения задач

Задача 1

Данные о количестве и общей полезности потребляемого блага приведены в таблице.

рассчитать предельную полезность;
построить график кривой общей и предельной полезности.

Решение

(a) Чтобы рассчитать предельную полезность каждой следующей единицы потребляемого блага воспользуемся следующей формулой:

Дальнейшие расчеты производились аналогично, а их результаты сведены в таблицу.

(b) Построим график на основании данных из предыдущей таблицы.

Как мы можем видеть предельная полезность блага равна нулю при потреблении 11 единиц, при этом потребителем достигается максимальная общая полезность 275 ютилей.