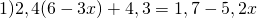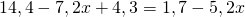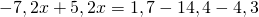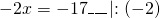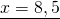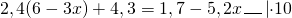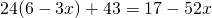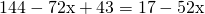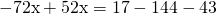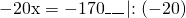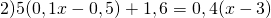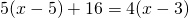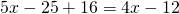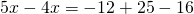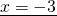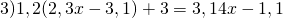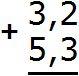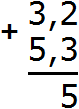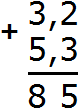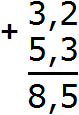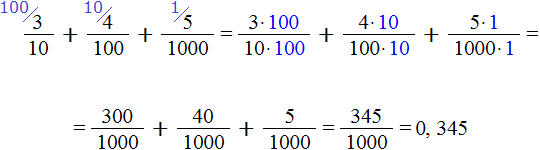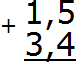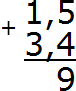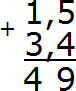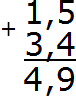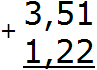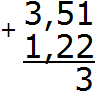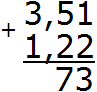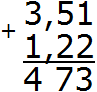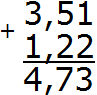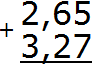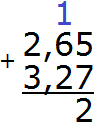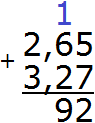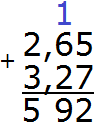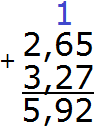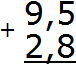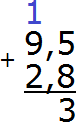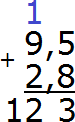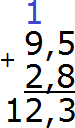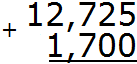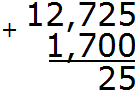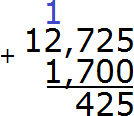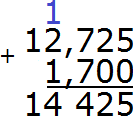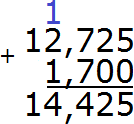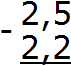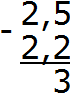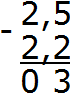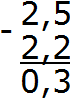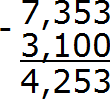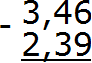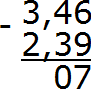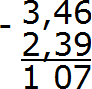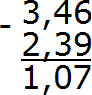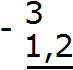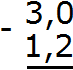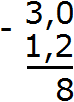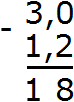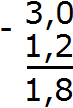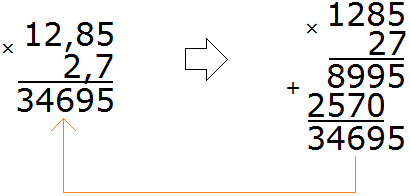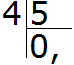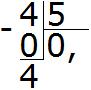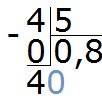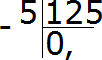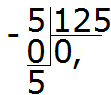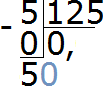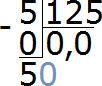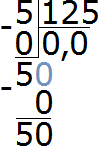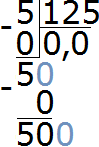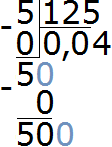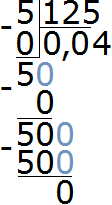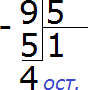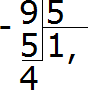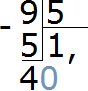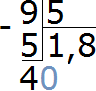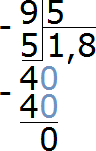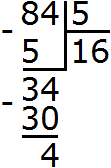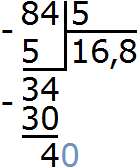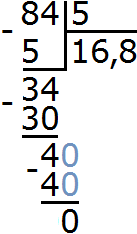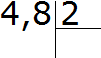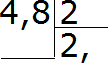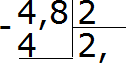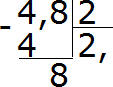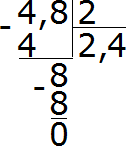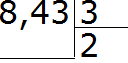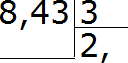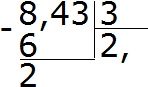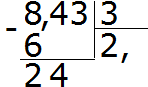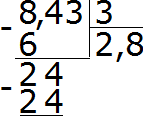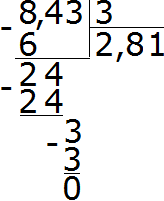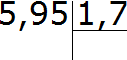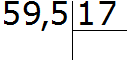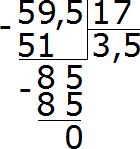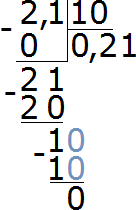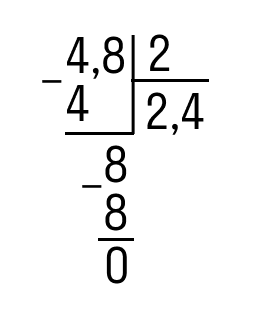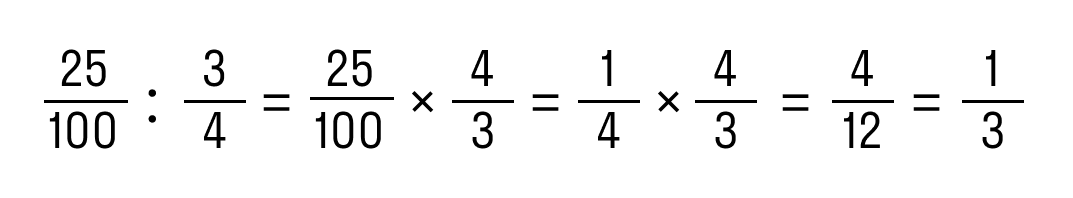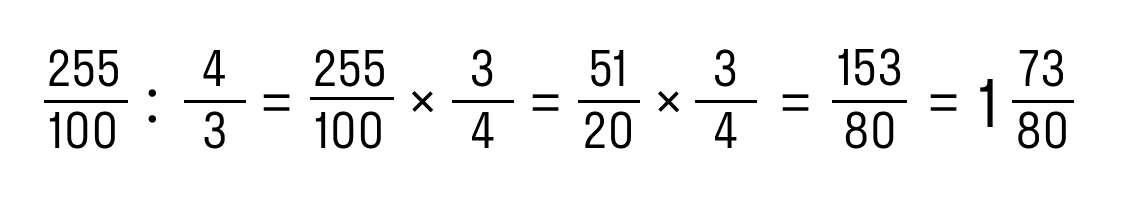Линейные уравнения с десятичными дробями можно решать так же, как и остальные линейные уравнения.
Однако, удобнее сначала уравнение упростить, избавившись от десятичных дробей.
Для начала рассмотрим оба способа решения и сравним их.
Раскрываем скобки. Так как перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках:
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Чтобы перевести десятичные дроби в целые числа, умножим обе части уравнения почленно на 10:
(При умножении произведения 2,4(6-3х) на 10 применяем сочетательное свойство умножения, то есть на 10 мы умножим только первый множитель, 2,4).
Получили линейное уравнение, которое не содержит десятичных дробей. Решаем его:
На мой взгляд, линейные уравнения с десятичными дробями удобнее решать, переводя их в уравнения с целыми числами.
Чтобы избавиться от десятичных дробей, обе части уравнения умножаем на 10. При этом в произведении 5(0,1х-0,5) на 10 умножаем второй множитель, то есть выражение в скобках, а в произведении 0,4(х-3) — первый, то есть 0,4:
Далее — решаем обычное линейное уравнение:
Обе части уравнения умножаем на 100. При этом в произведении 1,2(2,3х-3,1), надо первый множитель 1,2 умножить на 10 и второй множитель (2,3х-3,1) умножить на 10:
- Действия с десятичными дробями
- Сложение десятичных дробей
- Разряды в десятичных дробях
- Вычитание десятичных дробей
- Умножение десятичных дробей
- Умножение десятичной дроби на обычное число
- Умножение десятичных дробей на 10, 100, 1000
- Умножение десятичных дробей на 0,1 0,01 и 0,001
- Деление меньшего числа на большее. Продвинутый уровень.
- Деление чисел без остатка
- Деление десятичной дроби на обычное число
- Деление десятичной дроби на десятичную дробь
- Деление десятичной дроби на 10, 100, 1000
- Деление десятичной дроби на 0,1, 0,01 и 0,001
- Десятичные дроби
- Понятие десятичной дроби
- Свойства десятичных дробей
- Как записать десятичную дробь
- Как читать десятичную дробь
- Преобразование десятичных дробей
- Как перевести десятичную дробь в проценты
- Преобразование десятичных дробей
- Как перевести десятичную дробь в обыкновенную
- Действия с десятичными дробями
- Как разделить десятичную дробь на натуральное число
- Как разделить десятичную дробь на обыкновенную
- Как умножить десятичную дробь на обыкновенную
Видео:Сложение и вычитание десятичных дробей. 5 класс.Скачать

Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Видео:Сравнение десятичных дробей. 5 класс.Скачать
Сложение десятичных дробей
Как мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Видео:ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых 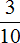
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых 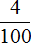
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных 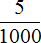
Если мы сложим дроби 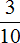
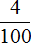
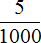
Сначала мы получили ответ 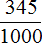
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Видео:Математика 5 кл Сложение и вычитание десятичных дробейСкачать

Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Видео:ДЕСЯТИЧНАЯ ДРОБЬ | сложение десятичных дробей | вычитание десятичных дробейСкачать

Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
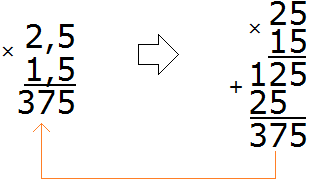
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
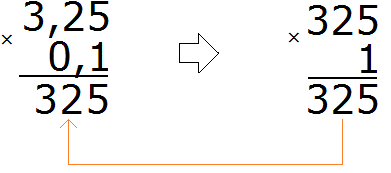
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Видео:Уравнение. 5 класс.Скачать

Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь 


Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби 
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
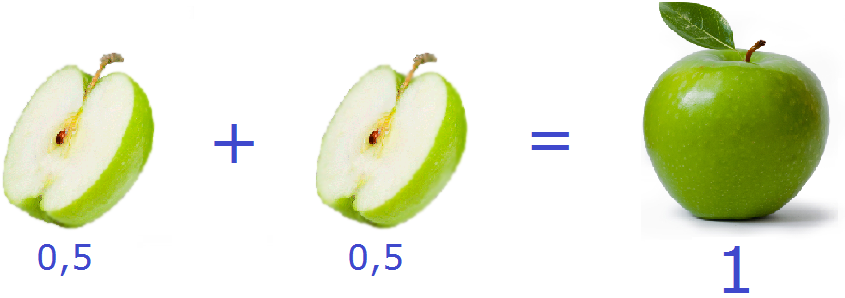
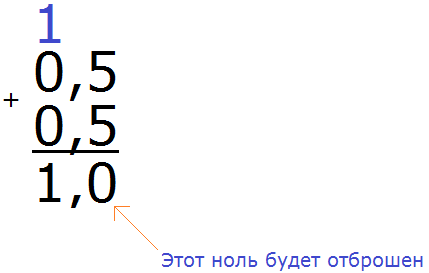
Получили ответ 0,5. Значит дробь 
Половину яблока 
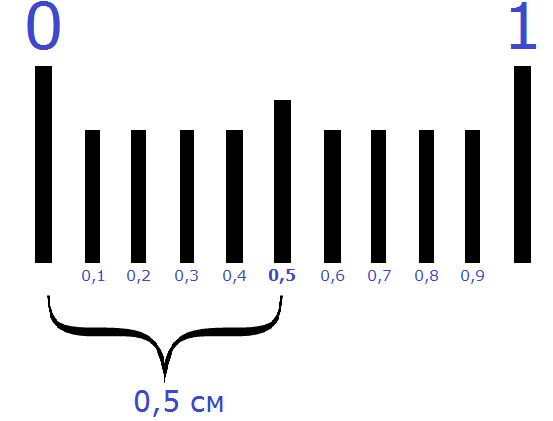
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Видео:УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке» .
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Видео:Действия с десятичными дробями 😈Скачать

Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело:
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Видео:Решение уравнений, 6 классСкачать

Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3 : 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
Видео:Перевод обыкновенной дроби в десятичную. Смотри, чтобы не ошибиться на экзамене!Скачать

Десятичные дроби
О чем эта статья:
5 класс, 6 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Видео:Деление десятичных дробей в столбик - примеры. Как делить в столбик десятичные дроби?Скачать

Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Пример 2. Перевести 37/1000 в десятичную дробь.
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.