Правила по уравнениям на умножение и деление

Большие затруднения для младшего школьника вызывает умение решать данный вид уравнений.

Мы уже знаем, что простые уравнения – это равенства, где есть одна переменная (неизвестное число).

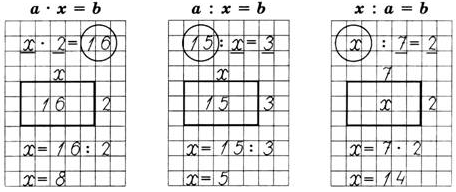
Во 2 классе дети учатся решать простые уравнения на умножение и деление (5 • х = 10, х: 3 = 12, 12 : х = 4)
Для решения этих уравнений правила о части и целом использовать нельзя, потому что второй множитель (х • 3 = 12) — это не часть, а число равных частей, на которое разбили целое.

Сегодня мы рассмотрим несколько вариантов решения:

1. Как никогда не путаться в выборе действий.

Если вы видите уравнение х: 4 = 8 и сомневаетесь, нужно х = 8 • 4 или х = 8 : 4, поступайте так: пишите на черновике простой пример на то действие, которое хочет вас запутать. Действие у нас – деление. Давайте напишем 6 : 2 = 3 и закроем число, которое в нашем уравнении неизвестно — это первое число, значит, закрываем число 6. И как шестерку найти, имея 2 и 3? Надо – перемножить тройку с двойкой. Значит, и в нашем уравнении нужно перемножать числа, но никак не делить:

Этот способ выручает, когда мы решаем вот такие уравнения: 4857 + у = 10208.
Большие числа часто пугают, а они живут по тем же законам, что и маленькие числа. Поэтому пишем, например 4 + 1 = 5. И закрываем число 1. Чтобы его найти, нужно из 5-и вычесть 1. Значит, 10208 – 4857:
у = 10208 — 4857
у = 5351

2. Зная правила нахождения стороны и площади прямоугольника.

3. Используя взаимосвязи между компонентами действий.

Этот способ необходим при ответе у доски.
Ученики младших классов обязаны овладеть математической речью, а для этого нужно знать, как называются компоненты при различных действиях:
Слагаемое, слагаемое, сумма.

Уменьшаемое, вычитаемое, разность.

Множитель, множитель, произведение.

Делимое, делитель, частное.

Например, в решении уравнения x • 3 = 6 объясняем так: чтобы найти первый множитель, надо значение произведения разделить на второй множитель.

В уравнении неизвестно слагаемое:

чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое:

4. Использование памятки:

Использовать памятку – самый простой и легкий способ решать простые уравнения правильно.

Данная памятка – результат многолетней работы в школе.

Поэтому вы можете ее скачать, распечатать и постоянно ей пользоваться.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 75

Видео:Решение уравнений на умножение и деление.Скачать

Математика. 3 класс

Конспект урока

Математика 3 класс

Урок № 45. Решение уравнений на основе связи между

результатами и компонентами умножения и деления

Перечень вопросов, рассматриваемых в теме:

1. Какие правила помогают решать уравнения? на основе взаимосвязи между
2. Как связаны результаты и компоненты умножения и деления?
3. Как проверить правильность решения уравнения?

Глоссарий по теме:

Уравнение – это равенство, содержащее переменную, значение которой надо найти

Множитель – это компонент умножения.

Произведение – это результат умножения и выражение а * b.

Делимое – компонент деления, число которое делят.

Делитель – компонент деления, число на которое делят.

Частное – это результат действия деления, а также выражение а : b

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 20.

1. Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с. 77.

Теоретический материал для самостоятельного изучения

Неизвестное число в математике обозначают буквой латинского алфавита, например икс. В математике такое равенство с переменной называют уравнение. Уравнение – это равенство, содержащее переменную, значение которой нужно найти, чтобы равенство было верным.

Если в уравнении неизвестен делитель, то, чтобы найти делитель, нужно делимое разделить на частное.

Если в уравнении неизвестно делимое, то, чтобы его найти, нужно делитель умножить на частное.

Если в уравнении неизвестен множитель, то, нужно произведение разделить на известный множитель.

Выполним тренировочные задания

№1. Выберите уравнение из предложенных равенств:

Ответ: х ∙ 5 = 40 – уравнение.

№2. К каждому уравнению первого столбца подберите соответствующее значение х.

№3. Выделите цветом уравнения, которые решаются делением.

№ 4. Расшифруйте фамилию писателя, расставляя ответы в порядке возрастания:

Видео:Математика 2 класс. «Уравнения на умножение и деление»Скачать

Правила по уравнениям на умножение и деление

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

• Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

• Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

• Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

• Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

• Чтобы найти неизвестное делимое, надо делитель умножить на частное.

• Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

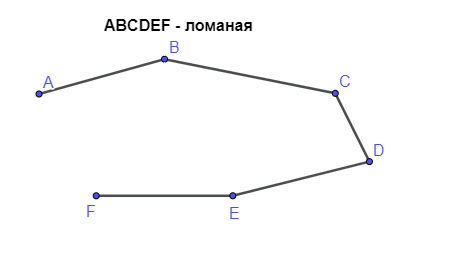
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

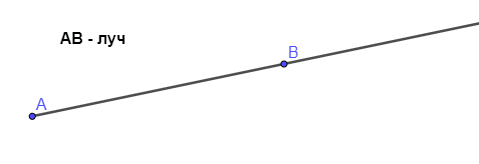
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

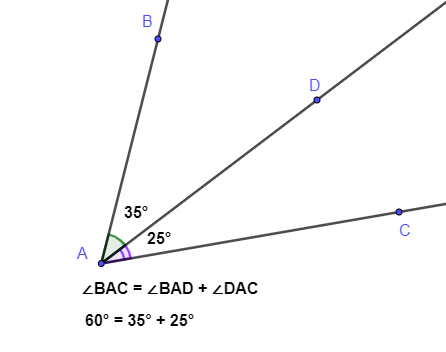
Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

• Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

• Если один из двух множителей равен 1, то произведение равно второму множителю.

• Если один из множителей равен нулю, то произведение равно нулю.

• Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

• Переместительный закон умножения:

• Сочетательный закон умножения:

• Распределительное свойство умножения относительно сложения:

• Распределительное свойство умножения относительно вычитания:

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

,

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

• ,

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

• ,

где — площадь основания параллелепипеда, — его высота.

Объем куба

,

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

• Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

• Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

• Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

• числитель разделить на знаменатель;
• полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

• целую часть числа умножить на знаменатель дробной части;
• к полученному произведению прибавить числитель дробной части;
• эту сумму записать как числитель неправильной дроби;
• в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

• с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
• после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

• все следующие за этим разрядом цифры отбросить.
• если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
• если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
• сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
• выполнить вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

• перемножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

V с р е д н я я = S о б щ t о б щ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Процент

Процентом называют сотую часть величины или числа 1%=

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Основные правила математики с примерами. 5 класс: 22 комментария

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.

Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖

📹 Видео

Математика 3 класс (Урок№45 - Уравнения на основе связи между результатами и компонентами "." и ":")Скачать

Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать

Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение уравнений на основе связи между результатами и компонентами умножения и деленияСкачать

Простые уравнения на умножение и деление. Легко объясняем детям, как решать уравнения.Скачать

Умножение и деление натуральных чиселСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Правила решения уравнений в 5 классе. Как запомнить и вывести их самому.Скачать

Решение уравнений (относительно умножения и деления). 5 классСкачать

Раскрытие скобок. 6 класс.Скачать

Математика 6 Умножение и деление положительных и отрицательных чиселСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Математика 3 Умножение и делениеСкачать

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Математика. 2 класс. Уравнения на умножение и деление /24.02.2021/Скачать