- Вопросы к параграфу
- Решаем устно
- Упражнения
- Упражнения для повторения
- Задача от мудрой совы
- Урок по теме «Уравнение» методическая разработка по математике (5 класс)
- Скачать:
- Предварительный просмотр:
- Правила по математике 5 класс мерзляк уравнения
- Основные правила математики с примерами. 5 класс: 22 комментария
- 📺 Видео
Вопросы к параграфу
1. Какое число называют корнем (решением) уравнения? — Корнем (решением) уравнения называют число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
2. Что значит решить уравнение? — Это значит найти все его корни или убедиться, что их вообще нет.
3. Как найти неизвестное слагаемое? — Надо из суммы вычесть известное слагаемое.
4. Как найти неизвестное уменьшаемое? — Надо к разности прибавить вычитаемое.
5. Как найти неизвестное вычитаемое? — Надо из вычитаемого вычесть разность.
Решаем устно
1. Найдите значение выражения 53 + х:
1. если х = 29, то 53 + х = 53 + 29 = 82
2. если х = 61, то 53 + х = 53 + 61 = 114
2. Найдите значение выражения 12y:
1. если: у = 7, то 12y = 12 • 7 = 84
2. если: у = 20, то 12y = 12 • 20 = 240
3. Найдите по формуле пути s = 50t расстояние (в метрах), которое проходит Петя:
1) за 4 мин: s = 50t = 50 • 4 = 200 метров
2) за 10 мин: s = 50t = 50 • 10 = 500 метров
Что означает числовой множитель в этой формуле? Числовой множитель 50 обозначает скорость движения Пети (м/мин).
4. Число а на 10 больше, чем число b. В виде каких из следующих равенств это можно записать:
- а + b = 10 — нельзя записать
- а — b = 10 — можно записать
- b — а = 10 — нельзя записать
- а — 10 = b — можно записать
- b + 10 = а — можно записать
Ответ: можно записать в виде равенств: а — b = 10; а — 10 = b; b + 10 = а.
5. Найдите все натуральные значения а, при которых выражение 20 : а принимает натуральные значения.
- если а = 1, то 20 : 1 = 20 — натуральное число
- если а = 2, то 20 : 2 = 10 — натуральное число
- если а = 4, то 20 : 4 = 5 — натуральное число
- если а = 5, то 20 : 5 = 4 — натуральное число
- если а = 10, то 20 : 10 = 2 — натуральное число
- если а = 20, то 20 : 20 = 1 — натуральное число
Ответ: при а = 1, 2, 4, 5 , 10 или 20.
6. На одну чашу весов поставили несколько гирь по 2 кг, а на другую — по 3 кг, после чего весы пришли в равновесие. Сколько поставили гирь каждого вида, если всего их поставили 10?
На одну чашу весов надо поставить 6 гирь по 2 кг, а на другую — 4 гири по 3 кг.
Для решения использовано 10 гирь.
Упражнения
267. Какое из чисел 3, 12, 14 является корнем уравнения:
1) х + 16 = 28
- если х = 3, то 3 + 16 = 19. Так как 19 ≠ 28, то число 3 не является корнем уравнения;
- если х = 12, то 12 + 16 = 28. Так как 28 = 28, то число 12 является корнем уравнения;
- если х = 14, то 14 + 16 = 30. Так как 30 ≠ 28, то число 14 не является корнем уравнения.
Ответ: корнем уравнения является число 12.
2) 4х — 5 = 7
- если х = 3, то 4 • 3 — 5 = 12 — 5 = 7. Так как 7 = 7, то число 3 является корнем уравнения;
- если х = 12, то 4 • 12 — 5 = 48 — 5 = 43. Так как 43 ≠ 7, то число 12 не является корнем уравнения;
- если х = 14, то 4 • 14 — 5 = 56 — 5 = 51. Так как 51 ≠ 7, то число 14 не является корнем уравнения.
Ответ: корнем уравнения является число 3.
268. Какое из чисел 3, 12, 14 является корнем уравнения:
1) 234 — y = 220
- если y = 3, то 234 — 3 = 231. Так как 231 ≠ 220, то число 3 не является корнем уравнения;
- если y = 12, то 234 — 12 = 222. Так как 222 ≠ 220, то число 12 не является корнем уравнения;
- если y = 14, то 234 — 14 = 220. Так как 220 = 220, то число 14 является корнем уравнения.
Ответ: корнем уравнения является число 14.
2) 72 : b + 13 = 19
- если b = 3, то 72: 3 + 13 = 24 + 13 = 37. Так как 37 ≠ 19, то число 3 не является корнем уравнения;
- если b = 12, то 72 : 12 + 13 = 6 + 13 = 19. Так как 19 = 19, то число 12 является корнем уравнения;
- если b = 12, то 72 : 12 + 13 = 5
+ 13 = 18
. Так как 18
≠ 19, то число 14 не является корнем уравнения.
Ответ: корнем уравнения является число 12.
269. Решите уравнение:
270. Решите уравнение:
271. Решите уравнение:
272. Решите уравнение:
273. Решите с помощью уравнения задачу.
1) Оксана задумала число. Если к этому числу прибавить 43 и полученную сумму вычесть из числа 96, то получим число 25. Какое число задумала Оксана?
Пусть задуманное Оксаной число равно x. Тогда можно составить уравнение:
96 — (х + 43) = 25
х + 43 = 96 — 25
х + 43 = 71
х = 71 — 43
х = 28
Ответ: Оксана задумала число 28.
2) У Буратино было 74 сольдо. После того как он купил себе учебники для школы, папа Карло дал ему 25 сольдо. Тогда у Буратино стало 68 сольдо. Сколько сольдо потратил Буратино на учебники?
Пусть Буратино потратил на учебники х сольдо. Тогда можно составить уравнение:
(74 — х) + 25 = 68
74 — х = 68 — 25
74 — х = 43
х = 74 — 43
х = 31
Ответ: Буратино потратил на учебники х сольдо.
274. Решите с помощью уравнения задачу.
Ваня задумал число. Если к этому числу прибавить 27 и из полученной суммы вычесть 14, то получим число 36. Какое число задумал Ваня?
Пусть задуманное Ваней число равно х. Тогда можно составить уравнение:
(х + 27) — 14 = 36
х + 27 = 36 + 14
х + 27 = 50
х = 50 — 27
х = 23
Ответ: Ваня задумал число 23.
275. Какое число надо подставить вместо а, чтобы корнем уравнения:
1) (x + а) — 7 = 42 было число 22
Подставим вместо х число 22 — корень уравнения, затем найдём неизвестное а:
(22 + а) — 7 = 42
22 + а = 42 + 7
22 + а = 49
а = 49 — 22
а = 27
Ответ: вместо а надо подставить число 27.
2) (а — x) + 4 = 15 было число 3
Подставим вместо х число 3 — корень уравнения, затем найдём неизвестное а:
(а — 3) + 4 = 15
а — 3 = 15 — 4
а — 3 = 11
а = 11 + 3
а = 14
Ответ: вместо а надо подставить число 14.
276. Какое число надо подставить вместо а, чтобы корнем уравнения:
1) (х — 7) + а = 23 было число 9
Подставим вместо х число 9 — корень уравнения, затем найдём неизвестное а:
(9 — 7) + а = 23
2 + а = 23
а = 23 — 2
а = 21
Ответ: вместо а надо подставить число 21.
2) (11 + х) + 101 = а было число 5
Подставим вместо х число 5 — корень уравнения, затем найдём неизвестное а:
(11 + 5) + 101 = а
16 + 101 = а
117 = а
а = 117
Ответ: вместо а надо подставить число 117.
Упражнения для повторения
277. Лиза была в школе с 8 ч 15 мин до 15 ч 20 мин. Вечером она пошла на тренировку. Там она провела на 5 ч 40 мин меньше времени, чем в школе. Сколько времени Лиза была на тренировке?
1) 15 ч 20 мин — 8 ч 15 мин = 7 ч 5 мин — Лиза провела в школе.
2) 7 ч 5 мин — 5 ч 40 мин = 6 ч 65 мин — 5 ч 40 мин = 1ч 25 мин — Лиа провела на тренировке.
Ответ: 1 ч 25 мин.
278. Начертите отрезок длиной 12 см. Над одним концом отрезка напишите число 0, а над другим — 480. Поделите отрезок на шесть равных частей. Отметьте на полученной шкале числа 40, 100, 280, 360, 420.
279. Можно ли, имея 900 р., купить 3 кг бананов по 65 р. за 1 кг, 2 кг мандаринов по 130 р. за 1 кг и 4 кг апельсинов по 95 р. за 1 кг?
Посчитаем общую стоимость предполагаемой покупки:
1) 65 • 3 = 195 (рублей) — потребуется на покупку бананов.
2) 130 • 2 = 260 (рублей) — потребуется на покупку мандаринов.
3) 95 • 4 = 380 (рублей) — потребуется на покупку апельсинов.
4) 195 + 260 + 380 = 835 (рублей) — будет стоить весь набор продуктов.
Сравним предполагаемую стоимость покупки с имеющейся суммой денег:
Значит купить все эти продукты на 900 рублей можно.
Задача от мудрой совы
280. В трёх ящичках лежат шары: в первом ящичке — два белых, во втором — два чёрных, в третьем — белый и чёрный. На ящички наклеены этикетки ББ, ЧЧ и БЧ так, что содержимое каждого из них не соответствует этикетке. Как, вынув один шар, узнать, что в каком ящичке лежит?
Этикетки на ящиках не соответствуют их содержимому. Значит в ящике БЧ не может лежать два разноцветных шарика. Там будет либо 2 белых шарика, либо два чёрных шарика. Вытащим один шар из ящика с этикеткой БЧ:
- если вытащен белый шар, то значит в ящике:
- БЧ — 2 белых шара;
- ББ — 2 чёрных шара;
- ЧЧ — 1 белый и 1 чёрный шар.
- если вытащен чёрный шар, то значит в ящике:
- БЧ — 2 чёрных шара;
- ББ — 1 белый и 1 чёрный шар;
- ЧЧ — 2 белых шара.
Ответ: надо вытащить шар из ящика с надписью БЧ.
Видео:Правила решения уравнений в 5 классе. Как запомнить и вывести их самому.Скачать

Урок по теме «Уравнение»
методическая разработка по математике (5 класс)
Подробная разработка урока математики в 5 классе по теме «Уравнения» УМК Мерзляк.
Видео:Уравнения. 5 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| tehnologicheskaya_karta_uroka_matematiki_v_5_klasse.docx | 622.72 КБ |
| marshrutnyy_list.docx | 58.62 КБ |
| rasstoyanie_mezhdu_naselennymi_punktami_zavyalovskogo_rayona_i_s.pdf | 197.16 КБ |
| uravneniya.pptx | 1.37 МБ |
Видео:Уравнение. 5 класс.Скачать

Предварительный просмотр:
ФИО: Архипова Евгения Андреевна
Место работы: МБОУ «Завьяловская СОШ №1 Завьяловского района».
Должность: Учитель математики и информатики.
Тема урока: «Уравнение».
Номер урока: 1 урок.
УМК: Мерзляк А. Г. Математика: 5 класс: учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — 2-е изд., перераб. – М.: Вентана-Граф, 2017. – 304 с.
Образовательная: формирование умения решать уравнения с использованием правил нахождения неизвестного компонента действий сложение и вычитание.
Воспитательная: воспитание самостоятельности, внимательности, уважения к работе товарищей.
Развивающая: развитие умения анализировать учебный материал, развитие умения слушать и вступать в диалог.
— повторить формулы для нахождения целого и его частей;
— формировать понятие «уравнение»;
— формировать понятие «корень уравнения»;
— формировать умение находить корень уравнения;
— повторить компоненты операций сложение и вычитание;
— формировать представление о том, что значит решить уравнение;
— формировать умение применять правила для нахождения неизвестного компонента.
Предметные: применение знаний для решения уравнений с помощью правил нахождения неизвестного компонента действий сложение и вычитание.
Личностные: формирование доброжелательного отношения к окружающим, умения проявлять познавательную инициативу в учебном сотрудничестве и планировать свои действия;
Метапредметные: формирование умения видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Формы работы учащихся: фронтальная, парная, индивидуальная.
Методы, технологии обучения:
Тип урока: изучение нового материала.
Основные понятия: уравнение, корень уравнения.
Метапредметные связи: география, история.
Оборудование: Компьютер, проектор, презентация на тему «Уравнение», раздаточный материал (маршрутные листы, фишки, сигнальные карточки).
Технологическая карта урока
Задания для учащихся, выполнение которые приведет к достижению запланированных результатов
Планируемые результаты УУД
Организационный этап (1 мин)
Цель: организация внимания учащихся, внутренней готовности к уроку.
-Активизирует внимание детей, нацеливая их на работу.
— Отмечает отсутствующих учащихся.
— Проверяет готовность учащихся к уроку.
— Занимают свои рабочие места.
— Называют отсутствующих в классе ребят.
— Проверяют наличие необходимых учебных принадлежностей.
Здравствуйте, ребята! Сегодня урок математики проведу у вас я, меня зовут Евгения Андреевна.
Но урок у нас будет не совсем обычный. Думаю, каждый из вас мечтает немного попутешествовать. Сегодня я приглашаю вас в путешествие по нашему району (Слайд 1), а поможет нам в этом мир математики.
Все ли у вас готово для путешествия (ручка, учебник, тетрадь и дневник)? Тогда я желаю вам хорошего урока и удачи!
создание благоприятного психологического климата на уроке.
формирование способности к самостоятельной организации рабочего места.
Мотивационный этап (6 мин)
Цель: подготовка мышления учащихся и организация осознания внутренней потребности к построению нового способа действий, постановка перед учащимися учебной проблемы.
— Предлагает учащимся подписать маршрутные листы.
— Для того чтобы узнать тему урока, организует работу над ребусом.
— Для составления плана путешествия рекомендует учащимся воспользоваться учебником.
— Внимательно изучают и подписывают маршрутные листы.
— Решая ребус, формулируют тему: «Уравнение» и цель урока: «Научиться решать уравнения».
— Составляют план путешествия, внимательно изучив материал параграфа:
1. Что называют уравнением?
2. Что значит «корень уравнения»?
3. Что значит «решить уравнение»?
4. Решать уравнения.
Перед вами на столах лежит маршрутный лист (Приложение 1) самооценки. Подпишите его. В ходе нашего путешествия, после выполнения каждого из заданий этого листа вы будите выставлять себе баллы, количество баллов за верно выполненный пункт указано в скобках.
Но для того, чтобы выстроить наш путь, необходимо определить, что же нам поможет в путешествии. Для этого вам необходимо разгадать следующий ребус: (Слайд 2)
Итак, ребята, что у вас получилось? Какова тема сегодняшнего урока?(Слайд 3)
А для чего нам нужно изучить эту тему? Чему мы будем учиться? Какова цель урока?
Запишите тему и цель в маршрутный лист.
А теперь давайте определим, с какими основными понятиями нам необходимо познакомиться. Составим план нашего путешествия, для этого откройте учебник на странице 69 пункт 10. Изучив материал учебника, выпишите основные понятия в маршрутный лист. (Слайд 4)
формирование умения высказывать собственную точку зрения в процессе обсуждения.
формирование умения самостоятельно формулировать тему и цель урока после предварительного обсуждения.
осуществление анализа объектов с выделением существенных признаков.
Актуализация опорных знаний, умений и навыков и получение новых.
Первичное закрепление полученных знаний (типовые задания) (15 мин)
Цель: приобретение новых знаний и установление уровня их усвоения, устранение обнаруженных проблем.
— Предлагает учащимся разбиться на пары и выполнить задание по предложенным схемам.
— С опорой на маршрутный лист и выполненные задания, предлагает самостоятельно сформулировать определение понятия «уравнение».
— Предлагает учащимся самостоятельно определить корень данного уравнения, и сформулировать следующее определение.
— Рассмотрев различные уравнения, предлагает определить, чем являются неизвестные величины и с опорой на маршрутный лист сформулировать правила.
— Работают в парах, выполняя задание предложенное учителем.
После выполнения один представитель от пары выписывает формулу на доску:
— Затруднение заключается в том, что неизвестна одна из частей.
— Данное задание можно выполнить, обозначив неизвестную часть за «x»:
— Формулируют определение понятия «уравнение» с опорой на маршрутный лист и выполненное задание.
— Внимательно изучив следующее задание и определив способ его выполнения, самостоятельно находят корень уравнения:
и с опорой на выполненное задание формулируют понятие «корень уравнения».
— Выполняя следующее задание, отвечают на вопросы учителя
Неизвестно слагаемое: 1, 2, 3, 4.
Неизвестно вычитаемое: 6, 7.
Неизвестно уменьшаемое: 5, 8.
и с опорой на материал, предложенный в маршрутном листе, формулируют правила нахождения неизвестного.
План готов, для того, чтобы посетить села и поселки нашего района будем следовать ему. И первое, что нам необходимо сделать это?
a)
Посмотрите на доску (Слайд 5). Обсудите в паре и запишите на листах формулы, с помощью которых можно найти:
— целое А, если известны части В и С.
— части В и С, если известно целое А и вторая часть.
б)
А теперь посмотрите на эту схему (Слайд 6,7) и аналогично запишите формулы, для нахождения целого и его частей.
Смогли ли вы выполнить это задание? В чем возникло затруднение?
Как можно решить данную проблему? А теперь составьте выражения по данной схеме.
Сформулируйте определение уравнения. Заполните пропуски в маршрутном листе.
И вот на горизонте показался первый населенный пункт, но чтобы узнать его название необходимо выполнить следующее задание (Слайд 8):
Являются ли числа 5, 13 корнем уравнения
x + 32 = 45.
Какое село мы посетили первым? Чтобы ответить на этот вопрос воспользуйтесь таблицей (Приложение 2).
Можем ехать дальше. Что необходимо сделать в следующем задании? (Слайд 9)
Запишите номера уравнений, в которых надо найти неизвестное слагаемое, уменьшаемое или вычитаемое.
1) 
5) 
2) 
6) 
3) 
7) 
4) 
8) 
И давайте вспомним правила, с помощью которых мы сможем найти это неизвестное. Сформулируйте их с опорой на маршрутный лист, заполнив пропуски.
формирование умения взаимодействовать с группой, умения слушать и слышать учителя.
планирование своего действия в соответствии с поставленной задачей и условиями реализации.
усвоение новых способов умственной деятельности через различные виды получения информации.
Физминутка (1 мин)
Мы совершили уже часть нашего путешествия, а теперь нам нужно отдохнуть (Слайд 10),
чтобы с новыми силами отправиться дальше:
Вверх рука, вниз рука
Потянулись мы слегка
Быстро поменяли руки,
Нам сегодня не до скуки.
Разминаем шею… стой.
А теперь встряхнулись лихо
И на стул садимся тихо.
— Предлагает учащимся решить по вариантам несколько уравнений, которые укажут названия посещенных населенных пунктов.
— В соответствии с вариантом, выполняют предложенное задание:
и в результате его выполнения формулируют ответ на вопрос: Что значит решить уравнение?
Пройдя долгий путь, мы вновь видим на горизонте несколько населенных пунктов, что же посетим на этот раз? (Слайд 11)
Решите уравнения и определите название населенного пункта, который вы посетили.
1) 
1) 
2) 
2) 
3) 
3) 
Итак, какие села или поселки мы посетили на этот раз?
Что значит решить уравнение?
Первичное закрепление нового материала (с измененной ситуацией) (10 мин)
Цель: закрепление умений и знаний, которые необходимы для самостоятельной работы по новому материалу.
— Предлагает учащимся выполнить задания в немного измененной ситуации, решение которых позволит узнать новые посещенные места.
— Контролирует процесс выполнения задания.
— Выполняют индивидуально задание, предложенное учителем, исправляя неверно решенные уравнения:
2) Решено неверно:



3) Решено неверно:
250 


Верное решение записывается учеником, который выполнил все быстрее остальных, на доске.
Верно. А выполнение следующего задания, позволит определить какие еще населенные пункты нам следует посетить.(Слайд 12)
1) 


2) 


3) 250 


Какие места нам еще нужно посетить?
Великая Отечественная война началась в 1941 году, и закончилась спустя 4 года после ее начала. После прошло еще несколько лет, и наступил 2020 год. Сколько лет прошло после окончания войны?
формирование умения высказывать собственную точку зрения в процессе обсуждения.
планирование своего действия в соответствии с поставленной задачей и условиями реализации.
формирование умения применять полученные знания в нестандартной ситуации.
Информация о домашнем задании (2 мин)
Цель: сообщение учащимся о домашнем задании, разъяснение методики его выполнения.
— Предлагает учащимся записать задания для домашней работы, объясняя методику его выполнения.
— Внимательно слушают и записывают домашнее задание в дневник.
Домашнее задание: (Слайд 13)
На оценку «3»: п. 10, № 268, 270.
На оценку «4», «5»: п. 10, № 270. Составить задачу на тему Завьяловского района, которая должна решаться с помощью уравнения.
формирование и углубление потребностей и мотивов учебно-познавательной деятельности.
Рефлексия (5 мин)
Цель: Цель: анализ и самооценка успешности достижения цели, результатов своей учебной деятельности.
— Отмечает степень вовлеченности учащихся в работу на уроке.
— Подводит итоги урока совместно с учащимися с помощью системы вопросов.
— Анализируют свою деятельность и формулируют конечный результат своей работы, отвечая на поставленные учителем вопросы.
Наше путешествие подошло к концу, а это значит, что настало время для подведения итогов занятия.
Чем мы занимались сегодня на уроке?
Какие села и поселки Завьяловского района смогли посетить?
Что нового вы узнали для себя?
Что вам понравилось больше всего?
Что получилось, а что еще требует дополнительного изучения?
Посчитайте, какое количество баллов вы набрали за все путешествие, и оцените себя в соответствии со следующей шкалой (Слайд 14):
Если ты набрал (ла):
13 – 11 баллов – «5»
10 – 8 баллов – «4»
формирование способности к самооценке на основе критерия успешности учебной деятельности.
формирование умения с достаточной полнотой и точностью выражать свои мысли.
Регулятивные:
формирование умения подводить итоги своей познавательной, учебной деятельности.
Маршрутный лист 24.10.19
Ф. И. __________________________________________
Тема: ___________________________________ (1 балл)
I. Работа в парах:
б) (1 балл)
II. Определение: (1 балл)
1. _______________________, в которых есть __________________ величина, называют уравнением .
III. Являются ли числа 5, 13 корнем уравнения x + 32 = 45. (1 балл)
Если x = 5 , то _________________________________________________________________________
Если x = 13 , то _________________________________________________________________________
IV. Определение*: (1 балл)
2. Корнем уравнения называют ___________________, которое при подстановке вместо буквы обращает уравнение в верное ________________ ___________________.
*если затрудняешься, смотри п. 10 на с.70 в учебнике.
V. Запишите номера уравнений: (1 балл)
1) 
5) 
2) 
6) 
3) 
7) 
4) 
8) 
а) Уравнения, в которых надо найти неизвестное слагаемое: ___________________________________
б) Уравнения, в которых надо найти неизвестное уменьшаемое ________________________________
в) Уравнения, в которых надо найти неизвестное вычитаемое __________________________________
VI. Заполни пропуски*: (1 балл)
1. Чтобы найти неизвестное слагаемое , надо из _______________ вычесть _______________ слагаемое.
2. Чтобы найти неизвестное уменьшаемое , надо к ________________ прибавить __________________.
3. Чтобы найти неизвестное вычитаемое , надо из ________________ вычесть ___________________.
*если затрудняешься, смотри п. 10 на с.70 в учебнике.
VII. Решите уравнения: (1 балл)
1) 
1) 
2) 
2) 
3) 
3) 
VIII. Определение: (1 балл)
3. Решить уравнение – значит _______________ все его ________________, или убедиться, что их нет.
IX. «Найди ошибку»: (1 балл за каждое верно решенное уравнение)
1) 





3) 250 


X. А можно ли… Составить уравнение**: (2 балла)
Великая Отечественная война началась в 1941 году, и закончилась спустя 4 года после ее начала. После прошло еще несколько лет, и наступил 2020 год. Сколько лет прошло после окончания войны?
**задача на дополнительные баллы.
XI. Задание на дом:
п. 10, № 270. Составить задачу на тему Завьяловского района, которая должна решать с помощью уравнения.
Если ты набрал (ла):
13 – 11 баллов – «5»
10 – 8 баллов – «4»
Оценка за урок: ____________
Расстояние между населенными пунктами Завьяловского района и
с. Чистоозёрка
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Правила по математике 5 класс мерзляк уравнения
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
Число меньше любого натурального числа.
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр
Свойства сложения
Переместительный закон:
Сочетательный закон:
Формула пути
= 50км,
= 2ч,
= 25км/ч
, 50км = 25км/ч· 2ч
, 25км/ч = 50км : 2ч
, 2ч = 50км : 25км/ч
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку
, то длина отрезка
равна сумме длин отрезков
и
.
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
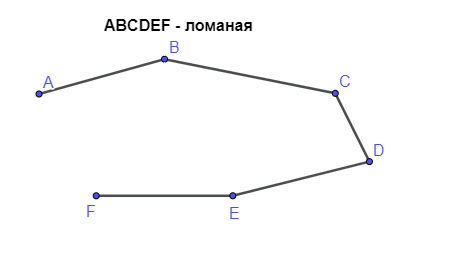
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
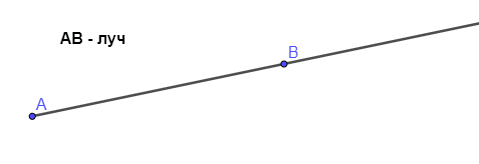
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
Равные углы
Два угла называют равными, если они совмещаются при наложении.
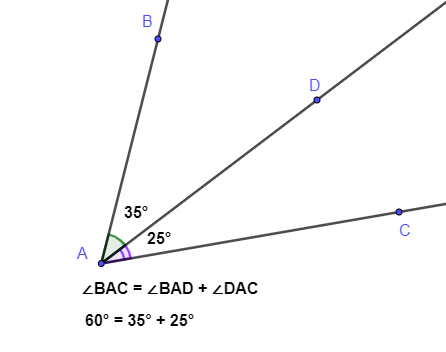
Свойство величины угла
Если между сторонами угла ∠ провести луч
, то градусная мера ∠
равна сумме градусных мер углов ∠
и ∠
, то есть ∠
= ∠
+ ∠
.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники. Равные фигуры
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр
вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и
, то его периметр
вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр
вычисляют по формуле
.
Умножение. Свойства умножения
Умножение
- Произведением числа
на натуральное число
, которое не равно 1, называют сумму, состоящую из
слагаемых, каждый из которых равен
. В равенства
числа
и
называют множителями, а число
и запись
— произведением.
- Если один из двух множителей равен 1, то произведение равно второму множителю.
- Если один из множителей равен нулю, то произведение равно нулю.
- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
- Распределительное свойство умножения относительно вычитания:
Деление. Деление с остатком
Деление
Для натуральных чисел равенство
является правильным, если является правильным равенство
В равенстве число
называют делимым, число
— делителем, число
и запись
— частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
,
Деление с остатком
, где
— делимое,
— делитель,
— неполное частное,
— остаток,
.
Если остаток равен нулю, то говорят, что число делится нацело на число
.
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
,
где — площадь квадрата,
— длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
,
где — объем параллелепипеда,
,
и
— его измерения, выраженные в одних и тех же единицах;
, где
— площадь поверхности прямоугольного параллелепипеда.
,
где — площадь основания параллелепипеда,
— его высота.
Объем куба
,
где — объем куба,
— длина его ребра.
Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.
- если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.
Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Найти среднее арифметическое чисел 15, 25 и 20.
15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20
Примечание:
Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.
V с р е д н я я = S о б щ t о б щ .
1) 200 + 120 = 320(км) -весь путь;
2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;
3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;
4) 4 + 4 = 8(ч) — все время;
5) 320 : 8 = 40(км/ч) — средняя скорость.
Процент
Процентом называют сотую часть величины или числа 1%=
Видео:ВСЯ математика 5-го класса в одном видео! Альфа-школаСкачать

Основные правила математики с примерами. 5 класс: 22 комментария
Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли
Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!
Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.
Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖
📺 Видео
Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Математика 5 класс. Уравнение. Корень уравненияСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Вся математика 5 класс за 1 час.Скачать

Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Как решают уравнения в России и СШАСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Уравнения со скобками - 5 класс (примеры)Скачать

КАК НАУЧИТЬСЯ СЧИТАТЬ ДРОБИ / ВСЕГО 3 ПРАВИЛАСкачать

Упрощение выражений. 5 класс.Скачать

Математика. 5 класс. Уравнение. Корень уравнения /15.09.2020/Скачать

Правило “весов”. Ещё один способ нахождения корня уравнения и не толькоСкачать

Основное свойство дроби. Сокращение дробей. 5 класс.Скачать

11. Уравнения (Виленкин, 5 класс)Скачать

Как умножать и делить дроби (Математика 5 класс)Скачать