Правила для уравнения при делении и умножении

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше ( )
меньше (

Видео:Решение уравнений на умножение и деление.Скачать

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо
• сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

• Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Видео:Математика порядок действий с умножением и делениемСкачать

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Видео:Математика 6 Умножение и деление положительных и отрицательных чиселСкачать

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

(4 + 1) * 3 + 36 : 3 — 7.

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.

Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.

Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!

Видео:Математика 3 класс (Урок№45 - Уравнения на основе связи между результатами и компонентами "." и ":")Скачать

Математика. 3 класс

Конспект урока

Математика 3 класс

Урок № 45. Решение уравнений на основе связи между

результатами и компонентами умножения и деления

Перечень вопросов, рассматриваемых в теме:

1. Какие правила помогают решать уравнения? на основе взаимосвязи между
2. Как связаны результаты и компоненты умножения и деления?
3. Как проверить правильность решения уравнения?

Глоссарий по теме:

Уравнение – это равенство, содержащее переменную, значение которой надо найти

Множитель – это компонент умножения.

Произведение – это результат умножения и выражение а * b.

Делимое – компонент деления, число которое делят.

Делитель – компонент деления, число на которое делят.

Частное – это результат действия деления, а также выражение а : b

Обязательная литература и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 20.

1. Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с. 77.

Теоретический материал для самостоятельного изучения

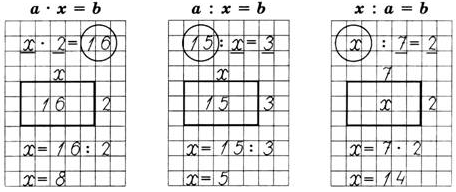
Неизвестное число в математике обозначают буквой латинского алфавита, например икс. В математике такое равенство с переменной называют уравнение. Уравнение – это равенство, содержащее переменную, значение которой нужно найти, чтобы равенство было верным.

Если в уравнении неизвестен делитель, то, чтобы найти делитель, нужно делимое разделить на частное.

Если в уравнении неизвестно делимое, то, чтобы его найти, нужно делитель умножить на частное.

Если в уравнении неизвестен множитель, то, нужно произведение разделить на известный множитель.

Выполним тренировочные задания

№1. Выберите уравнение из предложенных равенств:

Ответ: х ∙ 5 = 40 – уравнение.

№2. К каждому уравнению первого столбца подберите соответствующее значение х.

№3. Выделите цветом уравнения, которые решаются делением.

№ 4. Расшифруйте фамилию писателя, расставляя ответы в порядке возрастания:

Видео:Умножение рациональных чисел. 6 класс.Скачать

Простые уравнения на умножение и деление. 2 класс.

Большие затруднения для младшего школьника вызывает умение решать данный вид уравнений.

Мы уже знаем, что простые уравнения – это равенства, где есть одна переменная (неизвестное число).

Во 2 классе дети учатся решать простые уравнения на умножение и деление (5 • х = 10, х: 3 = 12, 12 : х = 4)
Для решения этих уравнений правила о части и целом использовать нельзя, потому что второй множитель (х • 3 = 12) — это не часть, а число равных частей, на которое разбили целое.

Сегодня мы рассмотрим несколько вариантов решения:

1. Как никогда не путаться в выборе действий.

Если вы видите уравнение х: 4 = 8 и сомневаетесь, нужно х = 8 • 4 или х = 8 : 4, поступайте так: пишите на черновике простой пример на то действие, которое хочет вас запутать. Действие у нас – деление. Давайте напишем 6 : 2 = 3 и закроем число, которое в нашем уравнении неизвестно — это первое число, значит, закрываем число 6. И как шестерку найти, имея 2 и 3? Надо – перемножить тройку с двойкой. Значит, и в нашем уравнении нужно перемножать числа, но никак не делить:

Этот способ выручает, когда мы решаем вот такие уравнения: 4857 + у = 10208.
Большие числа часто пугают, а они живут по тем же законам, что и маленькие числа. Поэтому пишем, например 4 + 1 = 5. И закрываем число 1. Чтобы его найти, нужно из 5-и вычесть 1. Значит, 10208 – 4857:
у = 10208 — 4857
у = 5351

2. Зная правила нахождения стороны и площади прямоугольника.

3. Используя взаимосвязи между компонентами действий.

Этот способ необходим при ответе у доски.
Ученики младших классов обязаны овладеть математической речью, а для этого нужно знать, как называются компоненты при различных действиях:
Слагаемое, слагаемое, сумма.

Уменьшаемое, вычитаемое, разность.

Множитель, множитель, произведение.

Делимое, делитель, частное.

Например, в решении уравнения x • 3 = 6 объясняем так: чтобы найти первый множитель, надо значение произведения разделить на второй множитель.

В уравнении неизвестно слагаемое:

чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое:

4. Использование памятки:

Использовать памятку – самый простой и легкий способ решать простые уравнения правильно.

Данная памятка – результат многолетней работы в школе.

Поэтому вы можете ее скачать, распечатать и постоянно ей пользоваться.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 75

💥 Видео

Умножение обыкновенных дробей и смешанных чисел. Практическая часть. 5 класс.Скачать

Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Раскрытие скобок. 6 класс.Скачать

Умножение и деление чисел с разными знаками (положительных и отрицательных чисел)Скачать

Решение уравнений (относительно умножения и деления). 5 классСкачать

Умножение и деление степеней. Алгебра, 7 классСкачать

КАК РАСКРЫТЬ СКОБКИ ПРИ УМНОЖЕНИИ, ДЕЛЕНИИ, ВЫЧИТАНИИ? Примеры | МАТЕМАТИКА 5 классСкачать

Как объяснить деление в столбик? Деление чисел уголком. Деление на многозначного на однозначное.Скачать

Решение уравнений, 6 классСкачать

Математика 2 класс. «Уравнения на умножение и деление»Скачать

8 класс, 3 урок, Умножение и деление алгебраических дробей. Возведение алгебраической дробиСкачать

Порядок выполнения действий в выражениях. Числовые выраженияСкачать

Как устно делить числа? Устное деление двузначного на двузначное. Как быстро решать примеры в уме?Скачать