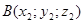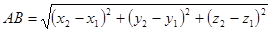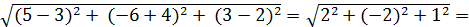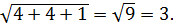Практическое занятие уравнение окружности сферы плоскости расстояние между точками

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение задач по теме: «Уравнение окружности, сферы, плоскости. Расстояние между точками»

— применить умения в использовании теоретических сведений для составления уравнений окружности, сферы, плоскости.

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

I Вариант II Вариант

1. Дан ∆ ABC с вершинами в точках Дан ∆ ABC с вершинами в точках

A (7; 3; -2) A (2; 0; 5)

B (1; 3; 6) B (3; 4; 0)

С (0; 0; -1). C (2; 4; 0).

Найти длину средней линии, Найти длину средней линии,

параллельной AB . параллельный BC .

2. Составить уравнение плоскости, Составить уравнение плоскости,

проходящей через точку А и проходящей через точку В и

перпендикулярный вектору AB , перпендикулярный вектору AB ,

если А(2; 3; -4), В(-1; 2; 2). если А(-2; 1; 3), В(1; -2; 4).

3. Сфера задана уравнением

( x -1) 2 + y 2 +( z -2) 2 = 9 x 2 +( y +3) 2 +( z -2) 2 = 25

a ) Назовите координаты центра и радиус сферы.

б) Определите, принадлежит ли данной сфере точки:

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

1.Расстояние между точками.

,

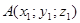
AB =

2. Уравнение плоскости.

Уравнение плоскости, проходящей через данную точку и перпендикулярной данному вектору.

Ненулевой вектор n, перпендикулярный плоскости, называют ее нормальным вектором. Если дана точка М(х₀;у₀; z ₀) и нормальный вектор n = (A, B, C) плоскости, то ее уравнение имеет вид A ( x — x ₀ ) + B ( y — y ₀) + C ( z — z ₀)

Равенство выражает необходимое и достаточное условие перпендикулярности двух векторов n и M ₀ M .

— уравнение окружности с центром в начале координат и радиусом r.

— уравнение окружности с центром в точке и радиусом r.

— уравнение сферы в точке с центром и радиусом R.

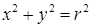
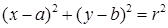
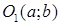
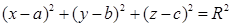
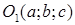
При выполнении практической работы рассмотрите следующие примеры:

Дан ∆АВС с вершинами в точках А(3; -4; 2), В(-5; 6; 7), С(5; -6; 3).

Найти длину средней линии, параллельной АС.

MN — средняя линия

AC =

=

Составить уравнение плоскости, проходящей через точку M (1; -2; 4) и перпендикулярный вектору MN , N (3; 4; 5).

MN=(3-1; 4+2; 5-4); MN=(2; 6; 1); a=2; b=6; c=1.

Сфера задана уравнением

( x +2) 2 +( y -5) 2 + z 2 =16.

а) Назовите координаты центра и радиус сферы.

б) Определите принадлежат ли данной сфере точки: А(-2; 9; 0) и В(1; 3; 2)

а) (-2; 5; 0) – координаты центра.

R = 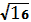= 4.

(-2+2) 2 +(9-5) 2 +0 2 =16

А принадлежит сфере.

(1+2) 2 +(3-5) 2 +2 2 =16

В не принадлежит 17=16 (неверно).

Вопросы для закрепления теоретического материала к практическому занятию:

1. Записать формулу расстояния между точками.

2. Уравнение плоскости.

3. Уравнение окружности.

4. Уравнение сферы.

Название практической работы.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7. Башмаков М.И. Математика: Учебник. — М., 2016.

Видео:Уравнение окружности, строим на координатной плоскостиСкачать

Практическая работа по математике для обучающихся 1 курса СПО по теме «Уравнение сферы, плоскости, прямой»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

ПРАКТИЧЕСКАЯ РАБОТА № 10

Составление уравнений сферы, плоскости, прямой.

Цели: формировать умение обучающихся решать задачи на данную тему; развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, воспитание трудолюбия, усердия в достижении цели, формировать общие компетенции ОК.2, ОК.3, ОК.4, ОК.5, ОК.6.

Справочный материал и примеры.

Теоретический материал для самостоятельного изучения:

Общее уравнение прямой имеет вид: Ax + By + C , где А, В, С – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: ( n _1; n ₂ ) Координаты точки ( х ₀ ; у ₀ ) .

Уравнение прямой по точке и направляющему вектору: Если известна некоторая точка, принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле: n ₁ ( x -х ₀ )+ n ₂ ( y -у ₀ )=0

Общее уравнение плоскости:

Общее уравнение плоскости имеет вид Ax + By + Cz + D =0 , где коэффициенты A , B , C , D одновременно не равны нулю.

Уравнение плоскости по точке и направляющему вектору: Если известна некоторая точка, принадлежащая плоскости, и вектор n, перпендикулярный этой плоскости (который называют вектором нормали к плоскости), то уравнение данной плоскости можно составить по формуле:

Уравнение поверхности сферы:

Сфера радиуса R с центром в начале координат представлена уравнением второй степени. x 2 + y 2 + z 2 = R 2 ( R – радиус сферы)

Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.

( x − a ) 2 +( y − b ) 2 +( z − c ) 2 = R 2 ( R — радиус сферы; a , b , c — смещение центра сферы относительно центра координат)

Задания для практической работы:

Составить уравнение сферы радиуса R = 5 с центром в начале координат.

Найти центр и радиус сферы (х+ 4) 2 + ( y —3) 2 + z 2 =100.

Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.

Составить уравнение прямой по точке и направляющему вектору М (4, -2), n (3,2)

Составить уравнение плоскости по точке Р (4, -2; -1) и вектору нормали, n (-5;3,-2)

Доказать, что уравнение х 2 + у 2 + z 2 —2х+ 4у—6 z + 5 = 0, является уравнением сферы.

Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).

Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору ВС, если А(-4; 2; -1), В(1; 2;-1), С(-2; 0; 1).

Какой вид имеет общее уравнение плоскости?

Какой вид имеет уравнение плоскости по точке и вектору нормали?

Какой вид имеет уравнение прямой по точке и направляющему вектору?

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Составление уравнений сферы, плоскости, прямой.
план-конспект занятия по геометрии (10, 11 класс)

Составление уравнений сферы, плоскости, прямой.

Видео:Уравнение окружности (1)Скачать

Скачать:

Видео:11 класс, 20 урок, Уравнение сферыСкачать

Предварительный просмотр:

Составление уравнений сферы, плоскости, прямой.

Цели: формировать умение обучающихся решать задачи на данную тему; развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, воспитание трудолюбия, усердия в достижении цели, формировать общие компетенции ОК.2, ОК.3, ОК.4, ОК.5, ОК.6.

Справочный материал и примеры.

Теоретический материал для самостоятельного изучения:

Общее уравнение прямой имеет вид: Ax + By + C , где А, В, С – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: ( n 1; n 2 ) Координаты точки ( х 0 ; у 0 ) .

Уравнение прямой по точке и направляющему вектору: Если известна некоторая точка, принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле: n 1 (x-х 0 )+n 2 (y-у 0 )=0

Общее уравнение плоскости:

Общее уравнение плоскости имеет вид Ax +By+Cz+D=0 , где коэффициенты A, B, C, D одновременно не равны нулю.

Уравнение плоскости по точке и направляющему вектору: Если известна некоторая точка, принадлежащая плоскости, и вектор n, перпендикулярный этой плоскости (который называют вектором нормали к плоскости), то уравнение данной плоскости можно составить по формуле:

A(x-х 0 )+B(y-у 0 )+C(z-z 0 )=0

Уравнение поверхности сферы:

Сфера радиуса R с центром в начале координат представлена уравнением второй степени. x 2 +y 2 +z 2 =R 2 (R – радиус сферы)

Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.

(x−a) 2 +(y−b) 2 +(z−c) 2 =R 2 (R — радиус сферы; a, b, c — смещение центра сферы относительно центра координат)

Задания для практической работы:

1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.
2. Найти центр и радиус сферы (х+ 4) 2 + (y —3) 2 + z 2 =100.
3. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.
4. Составить уравнение прямой по точке и направляющему вектору М (4, -2), n (3,2)
5. Составить уравнение плоскости по точке Р (4, -2; -1) и вектору нормали, n (-5;3,-2)
6. Доказать, что уравнение х 2 + у 2 + z 2 —2х+ 4у—6z+ 5 = 0, является уравнением сферы.
7. Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).
8. Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору ВС, если А(-4; 2; -1), В(1; 2;-1), С(-2; 0; 1).

1. Какой вид имеет общее уравнение плоскости?
2. Какой вид имеет уравнение плоскости по точке и вектору нормали?
3. Какой вид имеет уравнение прямой по точке и направляющему вектору?
4. Какой вид имеет общее уравнение прямой?
5. Какой вид имеет уравнение сферы?

🌟 Видео

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Расстояние между точкамиСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности. Расстояние между точками на плоскостиСкачать

9 класс, 7 урок, Уравнение прямойСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Длина отрезкаСкачать

Расстояние между двумя точками (прямоугольная система координат на плоскости).Скачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Расстояние между точками по координатам.Скачать

Расстояние между двумя точками. Координаты середины отрезка.Скачать

Расстояние между двумя точками с заданными координатамиСкачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать