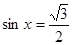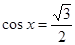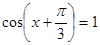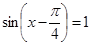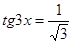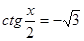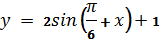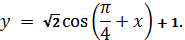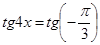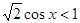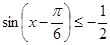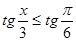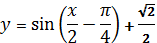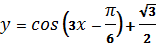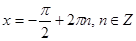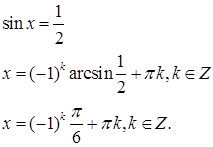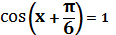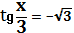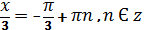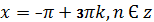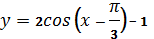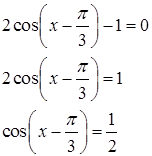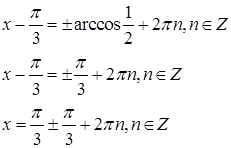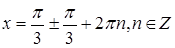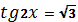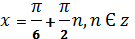Про уравнения - легко » Статьи

Практическое занятие решение тригонометрических уравнений и неравенств

Обновлено
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ — Тема: Решение простейших тригонометрических уравнений и неравенств.

Практическое занятие решение тригонометрических уравнений и неравенств

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение простейших тригонометрических уравнений и неравенств.

— применить умения по владению стандартными приемами решения тригонометрических уравнений и неравенств.

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

I Вариант II Вариант

а) Практическое занятие решение тригонометрических уравнений и неравенств

а) Практическое занятие решение тригонометрических уравнений и неравенств

б) Практическое занятие решение тригонометрических уравнений и неравенств

б) Практическое занятие решение тригонометрических уравнений и неравенств

в) Практическое занятие решение тригонометрических уравнений и неравенств

в) Практическое занятие решение тригонометрических уравнений и неравенств

2.Найти нули функции:

Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

3 . Решить уравнение и найти

его наименьший положительный корень

его наибольший отрицательный корень

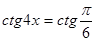
Практическое занятие решение тригонометрических уравнений и неравенств Практическое занятие решение тригонометрических уравнений и неравенств

4. Решить неравенства:

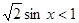
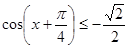
а) Практическое занятие решение тригонометрических уравнений и неравенства) Практическое занятие решение тригонометрических уравнений и неравенств

б) Практическое занятие решение тригонометрических уравнений и неравенствб) Практическое занятие решение тригонометрических уравнений и неравенств

в) Практическое занятие решение тригонометрических уравнений и неравенствв) Практическое занятие решение тригонометрических уравнений и неравенств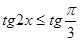

5. Найти значение x при которых график функции

Практическое занятие решение тригонометрических уравнений и неравенств

лежит ниже оси x

Практическое занятие решение тригонометрических уравнений и неравенств

лежит выше оси x

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

1. Из определения косинуса следует, что 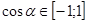Практическое занятие решение тригонометрических уравнений и неравенств. Поэтому, если а >1, то уравнение cosx = a не имеет решения. Например, уравнение cosx =-1,5 не имеет корней.

Если cosx =0, 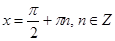Практическое занятие решение тригонометрических уравнений и неравенств.

Если cosx =-1, то х = π+2π n , n Є z .

Если cosx =1 , то x =2 πn , n Є z .

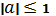
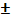
Если cosx = a , где Практическое занятие решение тригонометрических уравнений и неравенств,то x = Практическое занятие решение тригонометрических уравнений и неравенствarccos a + 2 πn , n Є z .

2.Из определения синуса следует, что

sin α Є [ -1; 1] . Поэтому уравнение

sin x = 3 не имеет корней.

Если sin x = 0 , то x = π n , n Є z .

Если sin x = 1 , то 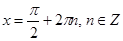Практическое занятие решение тригонометрических уравнений и неравенств.

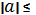
Если sin x = -1 ,то Практическое занятие решение тригонометрических уравнений и неравенств

sin x = a , Практическое занятие решение тригонометрических уравнений и неравенств1

x = (1) k arcsin a +πk , k Є z

3. Из определения тангенса следует , что tg x может принимать любое действительное значение. Поэтому уравнение tg x = a имеет корни при любом значении a .

x = arctg a + πn , n Є z

tg x = 0 , x = πn , n Є z

tg x = 1 , x = 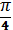Практическое занятие решение тригонометрических уравнений и неравенств+ πn , n Є z

tg x = -1 , x = — 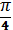Практическое занятие решение тригонометрических уравнений и неравенств+ πn , n Є z

4. Из определения котангенса следует, что ctgx может принимать любое значение. Поэтому уравнение ctgx = a имеет корни при любом значении а.

x = arcctg a + πn, n Є z.

5. Решения простейших тригонометрических неравенств выполняем с помощью единичной окружности.

При выполнении практической работы рассмотрите следующие примеры:

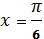
Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Ответ: Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств–наименьший положительный корень

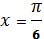
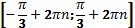
Найти нули функции Практическое занятие решение тригонометрических уравнений и неравенств

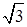
Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Ответ: Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств–наименьший положительный корень

Практическое занятие решение тригонометрических уравнений и неравенствx Є Практическое занятие решение тригонометрических уравнений и неравенств, n Є z

2 cosx Практическое занятие решение тригонометрических уравнений и неравенств;

cosx Практическое занятие решение тригонометрических уравнений и неравенств

x Є Практическое занятие решение тригонометрических уравнений и неравенств

в) sinx > Практическое занятие решение тригонометрических уравнений и неравенств

x Є Практическое занятие решение тригонометрических уравнений и неравенств

x Є Практическое занятие решение тригонометрических уравнений и неравенств

Вопросы для закрепления теоретического материала к практическому занятию:

1. Сформулируйте определение косинуса.

Запишите общую формулу решения уравнения cosx = a .

2. Сформулируйте определение синуса.

Запишите общую формулу решения уравнения sinx = a .

3. Запишите формулу решения уравнения tgx = a .

4. Перечислите алгоритм решения простейшего тригонометрического уравнения.

Название практической работы.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7. Башмаков М.И. Математика: Учебник. — М., 2016.

Содержание
  1. Методическое пособие для студентов. Решение тригонометрических уравнений и неравенств.
  2. «Чапаевский губернский колледж им. О. Колычева»
  3. Примеры решения задач
  4. Примеры решения задач
  5. 2. Примеры решения задач
  6. п.1 Решение тригонометрических уравнений,
  7. отличающихся от простейших
  8. При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:
  9. 1.Пробуем привести все тригонометрические функции к одному аргументу.
  10. 2.Если удалось привести к одному аргументу, то пробуем все тригонометрические выражения привести к одной функции.
  11. 3.Если к одному аргументу удалось привести, а к одной функции — нет, тогда пробуем привести уравнение к однородному.
  12. 4.В других случаях переносим все члены в одну сторону и пробуем получить произведение ил используем специальные приемы решения.
  13. п.2 Решение тригонометрических уравнений приведением к одной функции
  14. Примеры решения задач
  15. Примеры решения задач
  16. Примеры решения задач
  17. Урок-практикум «Решение тригонометрических уравнений и неравенств»
  18. 📽️ Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnline

Методическое пособие для студентов. Решение тригонометрических уравнений и неравенств.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практическое занятие решение тригонометрических уравнений и неравенств

Министерство образования и науки Самарской области

Министерство имущественных отношений Самарской области

Государственное бюджетное профессиональное

образовательное учреждение Самарской области

Видео:Как решать тригонометрические неравенства?Скачать

Как решать тригонометрические неравенства?

«Чапаевский губернский колледж им. О. Колычева»

Организация самостоятельной деятельности студентов при изучении темы «Решение тригонометрических уравнений и неравенств»

для студентов 1 курса по профессиям Сварщик (ручной и частично механизированной сварки (наплавки);

Практическое занятие решение тригонометрических уравнений и неравенств

гПрактическое занятие решение тригонометрических уравнений и неравенств.о.Чапаевск, 2017 г.

Публикуется на основании решения

ГБПОУ СОЧГК им. О. Колычева

Протокол № __8_от _20.04.2017

Организация самостоятельной деятельности студентов при изучении темы «Решение тригонометрических уравнений и неравенств» по дисциплине «Математика» для студентов 1 курса, И.В. Ямбаева – Чапаевск: ГБПОУ СОЧГК им.О. Колычева, 2017, 26 стр.- 15 экз.

Данное пособие включает в себя материал по организации самостоятельной деятельности студентов при выполнении заданий в ходе практических занятий по дисциплине «Математика», предназначено для преподавателей и студентов СПО.

Составитель: Ямбаева И.В., преподаватель математики высшей квалификационной категории

Рецензент: Ащепкова В.И., заведующий методическим кабинетом ОП СПО ППКРС, заслуженный учитель РФ

© ГБПОУ СО «Чапаевский губернский колледж

им.О. Колычева», 2017

Данный пособие предназначено для организации практических занятий при изучении темы: «Тригонометрические уравнения и неравенства». Оно поможет систематизировать имеющиеся знания и ликвидировать проблемы в них, если такие окажутся.

В сборнике содержится восемь основных тем, которые включают в себя справочный материал, тренинговые задания и задания для самостоятельный работы. Справочный материал содержит формулы и алгоритмы решения тригонометрических уравнений и неравенств. Эти разделы являются как бы консультантом по вопросам теории. Тренинговые задания содержат набор упражнений из учебника « Алгебра и начала анализа». А.Н.Колмогоров; -М.: Просвещение.

Задания для практических занятий составлены в соответствии с требованиями федерального государственного образовательного стандарта среднего профессионального образования к результатам усвоения данной темы.

Предлагаемый материал для сборника применяется преподавателем на уроках изучения темы «Тригонометрические уравнения и неравенства» и на уроках обобщающего повторения при подготовке к госэкзамену в конце второго курса.

Тема: Решение простейших тригонометрических

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

Примеры решения задач

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическая часть урока.

Решение №136,№137,№142б,г,№143в.( учебник Алгебра и начала анализа. А.Н.Колмогоров; -М.: Просвещение)

Урок. Практическое занятие. Решение тригонометрических уравнений cos x = a .

Образовательная цель урока: закрепить знания формул корней уравнения cos x = a, закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

1. Практическое занятие решение тригонометрических уравнений и неравенств12. 2cos (x + Практическое занятие решение тригонометрических уравнений и неравенств= 1

2. Практическое занятие решение тригонометрических уравнений и неравенств13. 2cos ( Практическое занятие решение тригонометрических уравнений и неравенств— Практическое занятие решение тригонометрических уравнений и неравенств= Практическое занятие решение тригонометрических уравнений и неравенств

3. Практическое занятие решение тригонометрических уравнений и неравенств14. cos ( Практическое занятие решение тригонометрических уравнений и неравенств— Практическое занятие решение тригонометрических уравнений и неравенств= Практическое занятие решение тригонометрических уравнений и неравенств

4. Практическое занятие решение тригонометрических уравнений и неравенств

5. 6. cos ( x — Практическое занятие решение тригонометрических уравнений и неравенств) = Практическое занятие решение тригонометрических уравнений и неравенств

7. cos ( 3x — Практическое занятие решение тригонометрических уравнений и неравенств) = Практическое занятие решение тригонометрических уравнений и неравенств

9. 10. 11. cos ( x + Практическое занятие решение тригонометрических уравнений и неравенств= Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу.

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

Примеры решения задач

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока.

Решение №138,№139,№142а,в,№143а ( учебник Алгебра и начала анализа. А.Н.Колмогоров; -М.: Просвещение)

Урок. Практическое занятие

Решение тригонометрических уравнений sin х = a .

Образовательная цель урока: закрепить знания формул корней уравнения sin х = a, закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

sin x = — Практическое занятие решение тригонометрических уравнений и неравенств

sin Практическое занятие решение тригонометрических уравнений и неравенств Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

sin ( x + Практическое занятие решение тригонометрических уравнений и неравенств) = Практическое занятие решение тригонометрических уравнений и неравенств

sin ( x — Практическое занятие решение тригонометрических уравнений и неравенств

sin (2 x + Практическое занятие решение тригонометрических уравнений и неравенств

sin (3 x — Практическое занятие решение тригонометрических уравнений и неравенств

2 sin ( Практическое занятие решение тригонометрических уравнений и неравенств

2 sin ( Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

3. Решение частных случаев тригонометрических уравнений

tg х= 1, х = Практическое занятие решение тригонометрических уравнений и неравенств+ Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств

tg х= 0, х = Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств,

tg х= -1, х = — Практическое занятие решение тригонометрических уравнений и неравенств+ Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств

с tg х= 1, х = Практическое занятие решение тригонометрических уравнений и неравенств+ Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств

с tg х= 0, х = Практическое занятие решение тригонометрических уравнений и неравенств+ Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств,

с tg х= -1, х = Практическое занятие решение тригонометрических уравнений и неравенств+ Практическое занятие решение тригонометрических уравнений и неравенствn , где n Практическое занятие решение тригонометрических уравнений и неравенств

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

10 класс, 23 урок, Методы решения тригонометрических уравнений

2. Примеры решения задач

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока. Решение №140,№141,№143б,г

Урок. Практическое занятие

Образовательная цель урока: закрепить знания формул корней уравнений tg t = a , с tg t = a , закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения.

2. ctg Практическое занятие решение тригонометрических уравнений и неравенств

3. tg (2x + Практическое занятие решение тригонометрических уравнений и неравенств

4. ctg (3x — Практическое занятие решение тригонометрических уравнений и неравенств

5. ctg (x + Практическое занятие решение тригонометрических уравнений и неравенств

6. tg (2x — Практическое занятие решение тригонометрических уравнений и неравенств

7. ctg (5x — Практическое занятие решение тригонометрических уравнений и неравенств

8. Практическое занятие решение тригонометрических уравнений и неравенствtg ( x — Практическое занятие решение тригонометрических уравнений и неравенств

9. Практическое занятие решение тригонометрических уравнений и неравенствctg ( x+ Практическое занятие решение тригонометрических уравнений и неравенств

10. ctg ( 2x — Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Урок. Примеры решения тригонометрических уравнений.

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэ

п.1 Решение тригонометрических уравнений,

Видео:ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрия

отличающихся от простейших

Материал для составления опорного конспекта:

Как правило, решение тригонометрических уравнений сводится к решению простейших уравнений с помощью преобразований тригонометрических выражений, разложения на множители и замены переменных. Если в уравнение, неравенство или тождество переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).

Практическое занятие решение тригонометрических уравнений и неравенств

При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:

1.Пробуем привести все тригонометрические функции к одному аргументу.

2.Если удалось привести к одному аргументу, то пробуем все тригонометрические выражения привести к одной функции.

3.Если к одному аргументу удалось привести, а к одной функции — нет, тогда пробуем привести уравнение к однородному.

4.В других случаях переносим все члены в одну сторону и пробуем получить произведение ил используем специальные приемы решения.

Практическая часть урока. Решение №164,165,166,167,168

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенства

п.2 Решение тригонометрических уравнений приведением к одной функции

Практическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока. Решение №169,170,171,172,173,

Урок. Практическое занятие

Решение тригонометрических уравнений.

Образовательная цель урока: закрепить знания способов решения уравнений , закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения:

а) 2 Практическое занятие решение тригонометрических уравнений и неравенств

б) 2 Практическое занятие решение тригонометрических уравнений и неравенств

в) 2 Практическое занятие решение тригонометрических уравнений и неравенств

г) 2 Практическое занятие решение тригонометрических уравнений и неравенств

а) 2 Практическое занятие решение тригонометрических уравнений и неравенств

б) Практическое занятие решение тригонометрических уравнений и неравенств

в) Практическое занятие решение тригонометрических уравнений и неравенств

г) Практическое занятие решение тригонометрических уравнений и неравенств

д) Практическое занятие решение тригонометрических уравнений и неравенств

е) Практическое занятие решение тригонометрических уравнений и неравенств

ж) Практическое занятие решение тригонометрических уравнений и неравенств

а) Практическое занятие решение тригонометрических уравнений и неравенств

б) Практическое занятие решение тригонометрических уравнений и неравенств

г) Практическое занятие решение тригонометрических уравнений и неравенств

д) Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Урок. Практическое занятие

Решение тригонометрических уравнений.

Образовательная цель урока: закрепить знания способов решения уравнений , закрепить умения применять полученные знания при решении уравнений различной степени сложности.

Задание 1. Решите уравнения:

Практическое занятие решение тригонометрических уравнений и неравенств16. Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств17. Практическое занятие решение тригонометрических уравнений и неравенств

3. Практическое занятие решение тригонометрических уравнений и неравенств18. 4 Практическое занятие решение тригонометрических уравнений и неравенств

4. Практическое занятие решение тригонометрических уравнений и неравенств19. 2Практическое занятие решение тригонометрических уравнений и неравенств

5. 2 Практическое занятие решение тригонометрических уравнений и неравенств

2 Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

2Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Тема: Решение простейших тригонометрических

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor online

Примеры решения задач

а) Практическое занятие решение тригонометрических уравнений и неравенствб) Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока. Решение №152,155,158б,159г.

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств вида cos t ≤ a , cos t ≥ a , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите уравнения.

1. cos x > — Практическое занятие решение тригонометрических уравнений и неравенств1 1 . 2 cos (2x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

2. cos 2 x > 0 1 2 . 2 cos (4x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

3. cos Практическое занятие решение тригонометрических уравнений и неравенств Практическое занятие решение тригонометрических уравнений и неравенств1

6. Практическое занятие решение тригонометрических уравнений и неравенств

7. Практическое занятие решение тригонометрических уравнений и неравенств

8. Практическое занятие решение тригонометрических уравнений и неравенств

9. 2 cos (x — Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

10. 2 cos (3x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств1

Домашнее задание: решение заданий по образцу

Урок . Решение неравенств вида

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенствx Практическое занятие решение тригонометрических уравнений и неравенств ( arc Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Видео:Решаем все типы задач № 12Скачать

Решаем все типы задач № 12

Примеры решения задач

аПрактическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств б) Практическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока.Решение №151,154,157а,в,158а,в.

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств вида sin t ≥ a , sin t ≤ a , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите неравенства:

1. sin x > — Практическое занятие решение тригонометрических уравнений и неравенств13. 2 sin (2x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

2. sin 2 x > 0 14. 2 sin (3x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств1

3. sin 6x Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

5. Практическое занятие решение тригонометрических уравнений и неравенств

6. Практическое занятие решение тригонометрических уравнений и неравенств

7. 2 Практическое занятие решение тригонометрических уравнений и неравенств

8. Практическое занятие решение тригонометрических уравнений и неравенств

9. 2 sin x + 1 Практическое занятие решение тригонометрических уравнений и неравенств0

10. 2 sin x — Практическое занятие решение тригонометрических уравнений и неравенств Практическое занятие решение тригонометрических уравнений и неравенств0

11. sin ( Практическое занятие решение тригонометрических уравнений и неравенств— x ) Практическое занятие решение тригонометрических уравнений и неравенств

12. 2 sin (x — Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Урок. Решение неравенств вида

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по Математике

Примеры решения задач

аПрактическое занятие решение тригонометрических уравнений и неравенств) tg x Практическое занятие решение тригонометрических уравнений и неравенствб) Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенств

3.Практическая часть урока. Решение №153,156,158г,159б,

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств , закрепить умения применять полученные знания при решении неравенств различной степени сложности.

Задание 1. Решите неравенства:

1. tg (x — Практическое занятие решение тригонометрических уравнений и неравенств

2. ctg (x + Практическое занятие решение тригонометрических уравнений и неравенств

3. tg ( 3x + Практическое занятие решение тригонометрических уравнений и неравенств

4. ctg (3x — Практическое занятие решение тригонометрических уравнений и неравенств

5. ctg (2x — Практическое занятие решение тригонометрических уравнений и неравенств

6. tg (2x – Практическое занятие решение тригонометрических уравнений и неравенств

7. Практическое занятие решение тригонометрических уравнений и неравенств

8. Практическое занятие решение тригонометрических уравнений и неравенств

9. 3 tg (2 x + Практическое занятие решение тригонометрических уравнений и неравенств) Практическое занятие решение тригонометрических уравнений и неравенств

10. √3 tg (6 x — Практическое занятие решение тригонометрических уравнений и неравенств

Домашнее задание: решение заданий по образцу

Урок. Практическое занятие

Решение неравенств, содержащих тригонометрические функции.

Образовательная цель урока: закрепить знания формул корней неравенств , закрепить умения применять полученные знания при решении неравенств различной степени сложности

Материал для составления опорного конспекта:

Практическое занятие решение тригонометрических уравнений и неравенств

Решите данное неравенство

Практическое занятие решение тригонометрических уравнений и неравенств

Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

2 Практическое занятие решение тригонометрических уравнений и неравенств

4Практическое занятие решение тригонометрических уравнений и неравенств

Sin 2x sin Практическое занятие решение тригонометрических уравнений и неравенств— cos 2x cos Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

Sin 3x cos x — Sin x cos Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

Урок. Контрольная работа №2: «Основы тригонометрии»

1. Решить уравнения

а) sin х = Практическое занятие решение тригонометрических уравнений и неравенств

б) cos Практическое занятие решение тригонометрических уравнений и неравенств= -1

в) ctg (2х + Практическое занятие решение тригонометрических уравнений и неравенств) = -1

г) 2 cos 2 х = 1+ sin х

д) 2 sin 2 х — 5 sinxcosx +3 cos 2 х = 0

е) cos 2 x + sinx =0

2. Решить неравенство

sinx Практическое занятие решение тригонометрических уравнений и неравенствПрактическое занятие решение тригонометрических уравнений и неравенств

1. Решить уравнения

а) cosx =Практическое занятие решение тригонометрических уравнений и неравенств

б) sin Практическое занятие решение тригонометрических уравнений и неравенств= 1

в) tg (3х +Практическое занятие решение тригонометрических уравнений и неравенств) = 1

г) 2 sin 2 = 1 — cosx

д ) 4sin 2 х — 5 sinxcosx +cos 2 x=0

е) cos 2 x + cosx =0

2. Решить неравенство

с osx Практическое занятие решение тригонометрических уравнений и неравенств—Практическое занятие решение тригонометрических уравнений и неравенств

Мальцев Д.А. «Алгебра 10-11 классы, тематические тесты и упражнения»,-Москва, НИИ школьных технологий, 2014г.

Дорофеев Г.В. «Сборник заданий для проведения письменного экзамена по математике за курс средней школы», -Москва, Дрофа, 2015г.

Видео:решение тригонометрических неравенств 3Скачать

решение тригонометрических неравенств 3

Урок-практикум «Решение тригонометрических уравнений и неравенств»

Разделы: Математика

Практическое занятие решение тригонометрических уравнений и неравенств

Современный уровень школьного образования характеризуется тем, что в рамках классно-урочной системы можно широко применять различные формы организации коллективной познавательной деятельности. Одной из таких форм – является групповая форма организации уроков-практикумов. При правильном педагогическом руководстве на таких уроках реализуются как учебные, так и воспитательные цели образовательного процесса, обеспечивающие:

  • высокий уровень усвоения учебного материала;
  • активность учебного процесса;
  • развитие обучающихся через совместную коллективную деятельность.

Практическое занятие решение тригонометрических уравнений и неравенств

На уроках-практикумах учащиеся рассаживаются за столом по 4–6 человек друг против друга, “глаза в глаза”. Исходя из целей, задач урока и уровня класса, группы могут формироваться, как одноуровневые, так и разноуровневые. Консультанта в каждой группе может назначать учитель или сама группа. Карточки – задания для групп могут быть разных вариантов с разным уровнем требований к математической подготовке. В группах идет обсуждение и поиск путей решения, работа с информационными источниками (учебники, справочники, конспекты уроков).

Проверка выполнения работы может выполняться по разному:

  • представители от групп работают за закрытой доской;
  • каждой группе дается образец решении для самопроверки.

Самоконтроль и взаимоконтроль с последующей самооценкой своих знаний и умений играет важную роль в развитии ребенка, формировании положительной “Я-концепции”.

Практическое занятие решение тригонометрических уравнений и неравенств

Учитель имеет возможность формировать характер общения в процессе взаимодействия “учитель и учащийся”, “учащийся и учащийся”, развивать коммуникативность и толерантность, умение и желание сотрудничать с другими людьми.

  1. Обобщить, систематизировать и сформировать прочные знания и умения учащихся по данной теме используя задания разного уровня сложности.
  • навыки коллективной деятельности;
  • умение выполнять взаимопроверку, самопроверку;
  • объективную самооценку своих знаний.
  • степень усвоения темы;
  • умение применять знания по данной теме для решения как стандартных, так и нестандартных задач.
  • умение объяснять, аргументировать свое решение, убедительно и обосновано доказывать свою точку зрения;
  • умение строить аналогии, обобщать и систематизировать;
  • умение рефлексировать;
  • интерес к предмету.
  • Ответственность и трудолюбие;
  • Коммуникативность и толерантность;
  • Уважительное отношение друг к другу.
  1. Организационный момент (5 мин.).
  2. Повторение теоретического материала (10 мин.).
  3. Работа в группах (45–70 мин.).
  4. Тестирование (15 мин.).
  5. Домашнее задание (2 мин.).
  6. Итог урока (3 мин.).

I . Организационный момент:

  • сообщение темы, цели и плана урока;
  • правила работы в группах;
  • критерии самооценки.

II . Повторение теоретического материла:

  1. Решая, тригонометрическое уравнение или неравенство, к чему мы стремимся в конечном итоге?
  2. Какие частные случаи мы выделяем среди простейших тригонометрических уравнений?
  3. Какие виды тригонометрических уравнений мы рассмотрели и каковы способы их решения?

III . Работа в группах:

А) № 1 проверяется устно;

Б) № 2 и № 3 проверяются по образцу каждой группой индивидуально, по мере выполнения заданий.

А) выполняется № 1–4;

Б) решаются № 1–4 за закрытой доской;

В) проверка заданий.

Выставление итоговой самооценки. (Приложение 1)

  1. Ю.А. Конаржевский “Анализ урока”, М., изд. “Педагогический поиск”, 2000 г.
  2. Дидактические материалы по алгебре и началам анализа под редакцией Л.О. Денищевой.
  3. Дидиктические материалы по алгебре и началам анализа под редакцией М.И. Шабунина.
  4. И.Т. Бородуля “Тригонометрические уравнения и неравенства”.
  5. П.И. Алтынов. Тесты “Алгебра и начала анализа”, 10–11.

📽️ Видео

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

Решение тригонометрических неравенств. Практическая часть. 10 класс.Скачать

Решение тригонометрических неравенств. Практическая часть. 10 класс.

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.

Тригонометрия в ЕГЭ может быть простойСкачать

Тригонометрия в ЕГЭ может быть простой

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.
Поделиться или сохранить к себе: