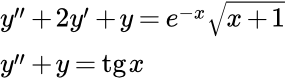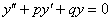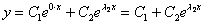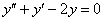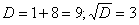Практическое решение дифференциальных уравнений второго порядка

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Практическое занятие «Решение дифференциальных уравнений второго порядка»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Учебная дисциплина ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

Тема урока Практическое занятие №24 «Решение дифференциальных уравнений второго порядка»

Закрепить усвоение теоретического материала по данной теме через решение упражнений;

Закрепить умения решать дифференциальные уравнения второго порядка.

Развитие качества ума, внимания, трудовых навыков студентов.

Воспитание познавательной активности, целеустремленности студентов.

Содержание практического занятия ориентировано на подготовку студентов к освоению профессиональных модулей ОПОП по специальности 230115 Программирование в компьютерных системах, и овладению профессиональными компетенциями (ПК):

ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.

ПК 2.4. Реализовывать методы и технологии защиты информации в базах данных.

ПК 3.4. Осуществлять разработку тестовых наборов и тестовых сценариев.

Оснащение урока варианты заданий

проверка отсутствующих, заполнение журнала.

Практическое занятие №24: выполнение практическое занятие №24.

Практическое занятие №24

«Решение дифференциальных уравнений второго порядка»

закрепить усвоение теоретического материала по данной теме через решение упражнений;

закрепить умения решать дифференциальные уравнения второго порядка.

Содержание практического занятия ориентировано на подготовку студентов к освоению профессиональных модулей ОПОП по специальности 230115 Программирование в компьютерных системах, и овладению профессиональными компетенциями (ПК):

ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.

ПК 2.4. Реализовывать методы и технологии защиты информации в базах данных.

ПК 3.4. Осуществлять разработку тестовых наборов и тестовых сценариев.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Это уравнения вида , где p и q – некоторые действительные числа.

Заменив в нем на , – на k и у – на , получим — характеристическое уравнение.

Вид общего решения уравнения (1) зависит от корней характеристического уравнения

Пример. Найти общее решение дифференциального уравнения: а) ; б) ; в) .

Для каждого из данных уравнений составляем характеристическое уравнение и решаем его. По виду полученных корней записываем общее решение дифференциального уравнения (см. табл.):

а) , корни – действительные и равные, поэтому общее решение уравнения ;

б) , , корни , – действительные и различные, поэтому общее решение уравнения ;

в) , корни – комплексно-сопряженные, поэтому общее решение уравнения .

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Это уравнения вида , его решение:.

Структура частного решения определяется правой частью уравнения

– многочлен степени

,

где

,

где

,

где

В таблице , , , , – известные числа, , – корни характеристического уравнения, , A , B – неизвестные коэффициенты, которые находятся путем подстановки в исходное уравнение (метод неопределенных коэффициентов).

Пример. Определить и записать структуру частного решения уравнения по виду функции , если а) ; б) .

Находим корни характеристического уравнения: , .

а) Так как , где , (случай 2 в табл. 2.2), то частное решение имеет вид .

, т. к. среди корней характеристического уравнения нет равных .

б) Поскольку (случай 3 в табл. 2.2): , , ), то ,

множитель появился потому, что является корнем характеристического уравнения.

Дифференциальные уравнения второго порядка, допускающие понижение порядка

1.Если дифференциальное уравнение имеет вид , то оно решается последовательным интегрированием.

2.Если в запись уравнения не входит функция y ( x ), т.е. оно имеет вид то такое уравнение можно решить, найдя вспомогательную функцию .

Пример: Решить уравнение .

Решение: Положим .

Исходное уравнение примет вид .

Это уравнение первого порядка с разделяющимися переменными.

Возвращаясь к первоначальной функции, получаем уравнение

3.Если в запись уравнения не входит переменная x , т.е. оно имеет вид то такое уравнение можно решить, найдя вспомогательную функцию .

Пример: Решить уравнение .

Решение: Положим . Исходное уравнение примет вид .

Это уравнение первого порядка с разделяющимися переменными.

Возвращаясь к первоначальной функции, получаем уравнение

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Вариант 1

Найти общее решение дифференциальных уравнений:

1) , 2) ; 3) .

Записать структуру частного решения линейного неоднородного уравнения по виду правой части.

а) ; б)

Найти общее решение дифференциальных уравнений:

1) ; 2) .

Найти общее решение дифференциального уравнения:

1) ; 2).

Найти решение дифференциального уравнения, допускающего понижение порядка.

1) , 2) , , .

Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Вариант 2

Найти общее решение дифференциальных уравнений:

1) ; 2) ; 3) .

Записать структуру частного решения линейного неоднородного уравнения по виду правой части:

а) ; б) .

Найти общее решение дифференциальных уравнений:

1) ; 2) .

Найти общее решение дифференциального уравнения:

1) ; 2).

Найти решение дифференциального уравнения, допускающего понижение порядка.

1) , 2) , , .

Видео:Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Вариант 3

Найти общее решение дифференциальных уравнений:

1) , 2) ; 3) .

Записать структуру частного решения линейного неоднородного уравнения по виду правой части.

а) ; б) .

Найти общее решение дифференциальных уравнений:

1) ; 2) .

Найти общее решение дифференциального уравнения:

1) ; 2)

Найти решение дифференциального уравнения, допускающего понижение порядка.

1) , 2) , , .

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Вариант 4

Найти общее решение дифференциальных уравнений:

1) ; 2) ; 3) .

Записать структуру частного решения линейного неоднородного уравнения по виду правой части.

а) ; б) .

Найти общее решение дифференциальных уравнений:

1) ; 2) .

Найти общее решение дифференциального уравнения:

1) ; 2).

Найти решение дифференциального уравнения, допускающего понижение порядка.

1) , 2) , , .

Подведение итогов урока: выводы, оценки, домашнее задание:

повторить методы решения дифференциальных уравнений второго порядка

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».

Изучить материал, составить конспект, выполнить задание, фото выполненной работы прислать в ВК.

Просмотр содержимого документа
«823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».»

Практическая работа по теме: «Решение дифференциальных уравнений II-го порядка»

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:

, где и – константы (числа), а в правой части – строго ноль.

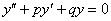
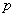
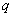
Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
, где и – константы, а – функция, зависящая только от «икс». В простейшем случае функция может быть числом, отличным от нуля.

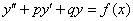
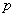
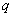
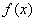
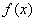
Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;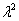
вместо первой производной записываем просто «лямбду»;
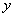
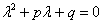
вместо функции ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

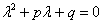
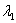
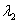
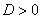
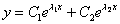
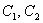
Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 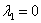, тогда общее решение:

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

,

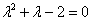
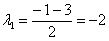
Ответ: общее решение:

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 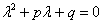имеет два кратных (совпавших) действительных корня (дискриминант ), то общее решение однородного уравнения принимает вид:
, где 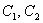– константы.
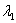
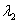
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

Если оба корня равны нулю , то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

Получены два кратных действительных корня

Ответ: общее решение:

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение 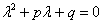имеет сопряженные комплексные корни , (дискриминант ), то общее решение однородного уравнения принимает вид:
, где 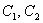– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:

– получены сопряженные комплексные корни

Ответ: общее решение:

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям ,

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня, поэтому общее решение:

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

Согласно начальному условию, получаем первое уравнение: или просто

Далее берём наше общее решение и находим производную:

Используем второе начальное условие :

Согласно второму начальному условию, получаем второе уравнение: или просто

Составим и решим систему из двух найденных уравнений:

Подставим найденные значения констант в общее решение :

Ответ: частное решение:

Найти общее решение дифференциального уравнения 2-го порядка.

Найти частное решение дифференциального уравнения 2-го порядка.

🎥 Видео

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Примеры решений дифференциальных уравнений 2 порядкаСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Дифференциальные уравнения. 11 класс.Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать