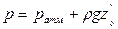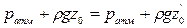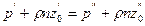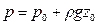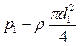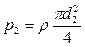Практическое применение основного уравнения гидростатики

Видео:Основы гидродинамики и аэродинамики | основное уравнение гидростатики | для взрослыхСкачать

Проект по физике учащихся 10 класса: «Законы гидростатики и их практические применения»

Ученический проект по физике»Законы гидростатики и их практическое применение»

Видео:Основное уравнение гидростатики (задачи)Скачать

Скачать:

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Предварительный просмотр:

Муниципальное казенное общеобразовательное учреждение

Новохоперского муниципального района

« Краснянская средняя общеобразовательная школа»

Проект по физике учащихся 10 класса:

и их практические применения»

Выполнили учащиеся 10 класса:

Учитель: Коломыцева Ольга Леонидовна

2016 учебный год.

1. Понятие Жидкости.

2. Основные свойства жидкости.

3. Понятие гидростатики. Гидростатическое давление. Свойства.

4. Основное уравнение гидростатики.

5. Примеры проявления и использования закона гидростатики.

Жидкость — одно из агрегатных состояний вещества. Основным свойством жидкости, отличающим её от других агрегатных состояний, является способность неограниченно менять форму под действием касательных механических напряжений, даже сколь угодно малых, практически сохраняя при этом объём.

Жидкое состояние обычно считают промежуточным между твёрдым телом и газом : газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое.

Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембрана. Так, вода может собираться в капли. Но жидкость способна течь даже под своей неподвижной поверхностью, и это тоже означает несохранение формы (внутренних частей жидкого тела).

Молекулы жидкости не имеют определённого положения, но в то же время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии.

Вещество в жидком состоянии существует в определённом интервале температур , ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло ), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления .

В технической гидромеханике под жидкостью понимают физическое тело, обладающее:

а) в отличие от твёрдого тела текучестью;

б) в отличие от газа весьма малой изменяемостью своего объёма.

Иногда жидкостью в широком смысле этого слова называют и газ; при этом жидкость в узком смысле слова, удовлетворяющую условиям а) и б) называют капельной жидкостью .

Основные свойства жидкости:

Основным свойством жидкостей является текучесть. Если к участку жидкости, находящейся в равновесии, приложить внешнюю силу , то возникает поток частиц жидкости в том направлении, в котором эта сила приложена: жидкость течёт. Таким образом, под действием неуравновешенных внешних сил жидкость не сохраняет форму и относительное расположение частей, и поэтому принимает форму сосуда, в котором находится.

В отличие от пластичных твёрдых тел, жидкость не имеет предела текучести : достаточно приложить сколь угодно малую внешнюю силу, чтобы жидкость потекла.

Одним из характерных свойств жидкости является то, что она имеет определённый объём (при неизменных внешних условиях). Жидкость чрезвычайно трудно сжать механически, поскольку, в отличие от газа , между молекулами очень мало свободного пространства. Давление, производимое на жидкость, заключенную в сосуд, передаётся без изменения в каждую точку объёма этой жидкости ( закон Паскаля , справедлив также и для газов). Эта особенность, наряду с очень малой сжимаемостью, используется в гидравлических машинах.

Жидкости обычно увеличивают объём (расширяются) при нагревании и уменьшают объём (сжимаются) при охлаждении. Впрочем, встречаются и исключения, например, вода сжимается при нагревании, при нормальном давлении и температуре от 0 °C до приблизительно 4 °C. А, например, тормозная жидкость в автомобилях, сжимается очень плохо.

Кроме того, жидкости (как и газы) характеризуются вязкостью . Она определяется как способность оказывать сопротивление перемещению одной из частей относительно другой — то есть как внутреннее трение.

Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением . Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул.

Жидкость в сосуде, приведённая в движение и предоставленная самой себе, постепенно остановится, но её температура повысится.

4.Образование свободной поверхности и поверхностное натяжение

Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы, например, воздух.

Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться.

Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости. Каждая молекула притягивает другие молекулы, стремится «окружить» себя ими, а значит, уйти с поверхности. Соответственно, поверхность стремится уменьшиться.

Поэтому мыльные пузыри и пузыри при кипении стремятся принять сферическую форму: при данном объёме минимальной поверхностью обладает шар. Если на жидкость действуют только силы поверхностного натяжения, она обязательно примет сферическую форму — например, капли воды в невесомости.

Маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади поверхности.

5.Испарение и конденсация

Испарение — постепенный переход вещества из жидкости в газообразную фазу (пар).

При тепловом движении некоторые молекулы покидают жидкость через её поверхность и переходят в пар. Вместе с тем, часть молекул переходит обратно из пара в жидкость. Если из жидкости уходит больше молекул, чем приходит, то имеет место испарение.

Конденсация — обратный процесс, переход вещества из газообразного состояния в жидкое. При этом в жидкость переходит из пара больше молекул, чем в пар из жидкости.

Испарение и конденсация — неравновесные процессы , они происходят до тех пор, пока не установится локальное равновесие (если установится), причём жидкость может полностью испариться, или же прийти в равновесие со своим паром, когда из жидкости выходит столько же молекул, сколько возвращается.

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением . Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V , т.е. P = G .

Если эту силу P разделить на площадь дна S abcd , то мы получим среднее гидростатическое давление , действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1 . В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Свойство 2 . Гидростатическое давление неизменно во всех направлениях.

Свойство 3 . Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Основным законом (уравнением) гидростатики называется уравнение:

p — гидростатическое давление ( абсолютное или избыточное) в произвольной точке жидкости,

z — высота точки над плоскостью сравнения (геометрический напор),

Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.

Иногда основным законом гидростатики называют принцип Паскаля .

Примеры проявления и использования закона гидростатики.

Открытие основного закона гидростатики — одно из крупнейших завоеваний античной науки. Чтобы оценить значение открытия, рассмотрим примеры проявления и использования этого закона в природе, широко известного как закон Архимеда.

Воды южных морей имеют более высокую соленость и плотность, чем воды арктического бассейна. Поэтому в Арктике нередки случаи, когда воды теплых течений опускаются под холодные воды северных широт. Например, в районе севернее Шпицбергена теплое южное течение опускается под холодные воды Ледовитого океана. Подобным же образом теплое течение Жаннетты, выходя из Берингова пролива, проходит под водами Арктики и выходит на поверхность лишь у берегов Северной Америки. Различная соленость вод имеет большое значение для возникновения течений и в южных широтах. В Мраморном море вода более соленая и быстрее испаряется, чем в Черном. Поэтому через Босфор в придонных слоях вода протекает из Мраморного моря в Черное, в поверхностных же слоях имеет место противоположное течение.

Подземные реки могут иметь выход не только на земную поверхность, но и на дно моря. Будучи более легкими, воды этих рек в неглубоком море могут подниматься до его поверхности, практически не смешиваясь с соленой водой. Подобные выходы пресных вод в открытом море имеются вблизи Марокканского побережья Атлантического океана (у Агадира) и в Коринфском заливе Ионического моря — вблизи Коринфа.

Поскольку средняя плотность тела рыб близка к плотности воды, их вес вблизи основных горизонтов жизнедеятельности достаточно хорошо уравновешивается выталкивающей силой по закону Архимеда. Благодаря ритмичной работе мышц рыба может отталкиваться от воды и таким образом перемещаться. При этом по ее телу в направлении от головы к хвосту с возрастающей амплитудой пробегает плоская или винтообразная упругая волна . Скорость распространения этой волны превышает быстроту перемещения рыбы. За счет ритмичного отталкивания от воды при распространении по телу упругой волны и осуществляется плавание рыб. К помощи плавников рыбы прибегают только для поддержания равновесия и при медленных перемещениях.

Такие обитатели морей, как осьминог, каракатица, моллюск сальпа, при перемещении используют принцип реактивного движения — они втягивают воду в специальные мускулистые мешки своего тела, а затем выталкивают ее наружу. Благодаря этому животные получают возможность перемещаться в направлении, противоположном выбрасываемой струе. А веслоногие, например черепахи, плавают, отталкиваясь от воды ногами.

Мелкие рыбы обычно движутся стаями. К этому их принуждает то обстоятельство, что при увеличении скорости движения близко расположенных тел по закону Бернулли понижается давление в пространстве между ними. Давление между каждыми двумя соседними рыбами в рыбьем косяке будет меньше, чем в среде, не возмущенной движением рыбьей стаи. В этом случае рыбы будут испытывать небольшую прижимающую их друг к другу силу и двигаться вместе. Если бы рыбы в косяке не подчинялись действию гидродинамических сил, они затрачивали бы больше энергии для своего перемещения.

В Средиземном море, у берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.

Живущий в тропических морях моллюск наутилус может быстро всплывать и вновь опускаться на дно. Моллюск этот живет в закрученной спиралью раковине. Когда ему нужно подняться или опуститься, он изменяет объем внутренних полостей в своем организме.

У широко распространенного в Европе водяного паука, обитающего в стоячих или слабо проточных водах, поверхность брюшка не смачивается водой. Уходя в глубину, он уносит с собой приставшую к брюшку воздушную оболочку, которая придает ему запас плавучести и помогает возвращению на поверхность.

Произрастающий в дельте Волги вблизи Астрахани чилим (водяной орех) после цветения дает под водой тяжелые плоды. Эти плоды настолько тяжелы, что вполне могут увлечь на дно все растение. Однако в это время у чилима, растущего в глубокой воде, на черешках листьев возникают вздутия, придающие ему необходимую подъемную силу, и он не тонет.

Известно, что наибольшие по размерам животные нашей планеты живут в воде. Закон Архимеда способствует тому, чтобы они не были раздавлены весом своего тела. В наше время самым крупным животным является кит, длина его может достигать 30 м. В мезозое крупнейшими были динозавры и среди них атлантозавр, длина тела которого составляла около 60 м.

Так как тела обитателей морей и рек содержат в своем составе много воды, давление в организме этих животных и в окружающей среде легко выравнивается. У рыб с плавательным пузырем такое уравнивание происходит лишь в сферах их постоянной жизнедеятельности. При быстром подъеме из области больших глубин на поверхность водоема плавательный пузырь рыб под действием высокого внутреннего давления выдавливается наружу, что приводит к их гибели.

В Мертвом море за счет большого количества растворенных солей (более 27% по весу) плотность воды достигает 1,16 г/см 3 . Купаясь в этом море, человек очень мало погружается в воду, находясь как бы на поверхности, поскольку средняя плотность тела человека меньше плотности воды. В нашей стране еще более высокая плотность воды наблюдается в заливе Кара-Богаз-Гол на Каспии и в озере Эльтон.

Для жизни под водой человек совершенно не приспособлен. На глубине 20 м под действием внешнего давления у него могут лопнуть барабанные перепонки. Опуститься же на глубину более 70 м без специального костюма человеку совершенно невозможно. (Правда, натренированные пловцы на очень короткое время опускаются под воду на глубину до 51 м).

В человеческом организме в полости живота давление немного превышает атмосферное, в полости груди, наоборот, меньше атмосферного. Если человек, находясь неглубоко под водой, попытается дышать через узкую трубочку (тростинку или соломинку ), то он может непродолжительное время это делать только при толщине находящегося над ним слоя воды менее 1 м. Дополнительное давление на человеческий организм столба воды в 1 м и более быстро приводит к полному прекращению дыхания и кровообращения. При этом кровь переполняет сердце, а брюшная полость и ноги почти совершенно обескровливаются. В процессе же ныряния жизнедеятельность человека существенным образом не нарушается, поскольку в этом случае он набирает в легкие дополнительное количество воздуха, которое помогает ему уравновешивать давление воды на его организм.

Известный русский адмирал М.П. Лазарев неоднократно показывал матросам во время плаваний следующий любопытный опыт с бутылкой. С помощью свинцового груза порожнюю закупоренную бутылку матросы опускали под воду на глубину до 430 м. После ее подъема на палубу они с удивлением убеждались, что бутылка заполнена глубинной водой и плотно закрыта пробкой, причем верх и низ пробки поменялись местами. Это происходило за счет давления воды, которое, в соответствии с законами гидродинамики, на глубине 430 м имеет вполне достаточную для этого величину. Опыт Лазарева представляет собой яркую демонстрацию действия давления воды на больших глубинах. Это позволяет лучше понять действие давления воды и на человеческий организм.

Многим, наверное, не раз приходилось наблюдать ледоход на реках. Еще более грандиозное зрелище представляют собой айсберги — «плавучие ледяные горы» больших размеров. Айсберги — это массы материкового льда, оторвавшиеся от ледника или ледового барьера и плавающие в полярных морях и прилегающих к ним акваториях.

Средняя высота надводной части айсберга нередко достигает 50. 70 м, максимальное ее значение приближается к 450 м. Наибольшая длина подводной части может доходить до 130 км. Объем надводной части айсберга составляет небольшую часть его полного объема.

Перемещаясь в более теплые воды, айсберг оплавляется снизу, в результате чего центр тяжести его перемещается выше центра, к которому приложено выталкивающее действие воды. Такой айсберг теряет равновесие и с шумом переворачивается.

При спокойном море и отсутствии ветра айсберг с подтаявшей нижней частью начинает раскачиваться, что является признаком предстоящего переворачивания. Когда айсберг находится в состоянии неустойчивого равновесия, даже работа машин находящегося поблизости корабля может дать толчок к переворачиванию.

Таяние айсбергов на южной границе северных морей вызывает некоторое понижение солености воды. В этом же районе в процессе таяния айсберги сбрасывают на дно морей захваченные ими части морен, а иногда и довольно крупные куски скал.

В средней полосе Советского Союза имеются следы подобной деятельности айсбергов, относящиеся к периоду, когда территория нашей страны была дном моря. Аналогично происходит вынос окатанной гальки на дно арктического бассейна. Примерзая ко льду у берегов, галька вместе с льдинами уносится впоследствии в океан и опускается на его дно после таяния льда.

В некоторых реках при быстром течении за счет интенсивного перемешивания воды происходит переохлаждение отдельных участков дна. При этом переохлажденный участок дна покрывается льдом внутриводного и отчасти поверхностного происхождения. Иногда донный лед занимает значительную часть сечения реки. Тогда река выходит из берегов, и становится возможным наводнение.

Так как подъемная сила льда пропорциональна его объему, а сила сцепления с ложем реки пропорциональна поверхности, то при отложении достаточно большого количества льда на дне он может преодолеть сцепление с ложем и всплыть на поверхность. Поднявшаяся на поверхность губчатая масса донного льда обычно содержит различные включения: камни, песок, а иногда и затонувшие якоря вместе с якорными цепями. Донный лед может возникать не только на реках, но и в неглубоких местах морей и озер (вблизи берегов), где переохлаждение достигает дна водоема. В этом случае всплывающий лед поднимает на поверхность придонные водоросли.

Искусно используют закон Архимеда подводники. Если подводная лодка плывет между слоями воды с разной температурой, ее балласт подбирают таким образом, чтобы обеспечить небольшую перегрузку для теплого слоя и недогрузку для холодного. В этом случае лодка лежит на холодном слое, не нуждаясь в специальных мерах для поддержания равновесия. Для батискафа с небольшой отрицательной плавучестью слой более плотной воды может играть роль уравновешивающего «жидкого грунта».

При переходе подводной лодки из морских глубин в устье реки, подводники тщательно следят за расстоянием между лодкой и дном, так как в пресной воде выталкивающая сила Архимеда меньше, чем в морской, и при недосмотре со стороны экипажа лодка может сесть на илистый грунт речного устья.

Очень большое значение закон Архимеда имеет в технике бурения. Буровая колонна для бурения глубоких скважин уже на глубине 5 км в воздухе имела бы вес 226 тонн. Однако в промывочной жидкости плотностью 2 г/см 3 в соответствии с законом Архимеда вес буровой колонны будет сильно уменьшен. Алюминиевые трубы «теряют» в весе в этих условиях до 50%. Подбором промывочной жидкости можно намного уменьшить вес буровой колонны. Это в огромной степени способствует успеху бурения.

Видео:Практическое применение гидродинамикиСкачать

Практическое использование законов гидростатики

Применив закон Паскаля к сообщающимся сосудам, можно прийти к следующим выводам.

Если сосуды (рис. 1.4 а) заполнены однородной жидкостью (одинаковой плотности), то при равновесии давление в точке 0 может быть выражено:

либо ,

т.е. в сообщающихся сосудах заполняющая их однородная жидкость располагается на одинаковом уровне.

При заполнении сосудов жидкостями с различной плотностью (рис 1.4 б) в условиях равновесия давление в точке О будет

либо .

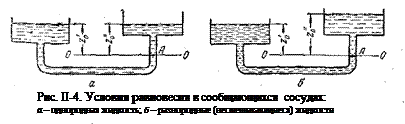
Рисунок 1.4 – Сообщающиеся сосуды, заполненные жидкостью:
а – одной плотности; б – разной плотности

Следовательно , т.е.

. (1.12)

Соотношение (1.12) указывает на то, что высоты уровней жидкости, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.

Этот принцип используется для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стёкол, в жидкостных манометрах.

Если сообщающиеся сосуды заполнены одной и той же жидкостью, но давление над уровнем жидкости в них разное – р₁ и р₂, то при равновесии

,

,

. (1.13)

Последнее выражение используется при измерении давления или разности давлений между различными точками с помощью дифференциальных U-образных манометров.

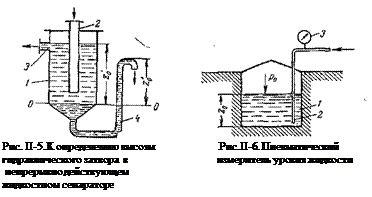
Рисунок 1.5. – К определению высоты гидравлического затвора

Этот же принцип используется для определения высоты гидравлического затвора в аппаратах, заполненных жидкостью (рис. 1.5).

На рисунке представлен сосуд, заполненный двумя жидкостями с плотностями r₁ и r₂; уровень их раздела на глубине z₁ необходимо поддерживать в процессе работы постоянным с помощью гидрозатвора, представляющего собой U-образную трубку, подсоединённую снизу (на выходе жидкости из аппарата).

В соответствии с уравнением (1.12) высота гидравлического затвора в случае одинакового давления над жидкостью внутри аппарата и на выходе из затвора

. (1.14)

На использовании данного уравнения гидростатики основана работа таких простейших гидравлических машин, как гидравлический пресс, мультипликатор (для повышения давления), домкрат, подъемник и др.

Рисунок 1.6 – Схема гидравлического пресса

На рис. 1.6 показана схема гидравлического пресса. Если к поршню П₁, имеюшему площадь F₁, приложена сила Р₁, то эта сила будет передаваться на жидкость; жидкость же будет давить на поршень П₂, имеющий площадь F₂, с силой Р₂

(1.15)

так как гидростатические давления в точках площади F₁ и площади F₂ практически равны между собой:

(1.16)

Из уравнения (1.16) следует, что при помощи пресса сила Р₁ увеличивается во столько раз, во сколько площадь F₂ больше площади F₁.

Элементы гидродинамики

Основной задачей гидродинамики является установление закономерностей, определяющих движение потока жидкости, а также его отдельных частиц.

При рассмотрении движения жидкости различают внешнюю и внутреннюю задачи. В первом случае задан поток, требуется найти гидродинамические характеристики потока. К числу гидродинамических характеристик потока относятся скорость и гидродинамическое давление.

В случае идеальной жидкости гидродинамическое давление имеет тот же смысл и обладает теми же свойствами, что и гидростатическое давление р. Гидростатическое давление вязкой жидкости зависит от пространственной ориентации площадки, на которую она действует, поэтому при анализе движения в этом случае используют среднеарифметическое значение:

. (1.17)

Помимо сил, действующих на покоящуюся жидкость, в гидродинамике появляются дополнительно силы инерции и трения. Последние являются причиной неравенства скоростей w в различных точках одного и того же поперечного сечения потока. Кроме того, для одной и той же точки пространства р и w могут изменяться и во времени τ.

Указанные причины приводят к сложным функциональным зависимостям:

(1.18)

, (1.19)

Основные понятия и определения

Различают следующие виды движения жидкости: установившееся и неустановившееся, равномерное и неравномерное, напорное и ненапорное.

Если в любой точке движущегося потока жидкости все факторы, влияющие на его движение (скорость, давление, температура, плотность и др.) не изменяются с течением времени, то движение потока называют установившимся. При неустановившемся движении указанные факторы с течением времени изменяются.

Установившиеся условия движения жидкости характерны для непрерывных технологических процессов, неустановившиеся – для периодических либо возникают кратковременно при пусках, остановках, а также изменениях режима работы аппаратов непрерывного действия.

Для каждой частицы движущейся жидкости изменение её параметров во времении в пространстве выражается полной производной по времени, называемой субстанциональной производной. Иначе субстанциональная производная характеризует изменение какого-либо параметра u или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве. Изменение u за единицу времени в фиксированной точке пространства (x, y, z) = const выражается частной производной , а изменение u в данной точке за бесконечно малый промежуток времени составит . Эта величина является местным, или локальным, изменением данной переменной. При переходе частицы из одной точки в другую значение u меняется на величину , которая характеризует конвективное изменение параметра u.

При установившемся движении жидкости локальная составляющая отсутствует, и субстанциональная производная принимает вид:

, (1.20)

. (1.21)

Для неустановившегося движения полное изменение u является суммой локального и конвективного изменения:

. (1.22)

Видами установившегося движения жидкости являются равномерное и неравномерное движение потока.

Под равномерным понимают такое движение, когда поток жидкости по всей его длине имеет одинаковые живые сечения и скорости в соответствующих точках этих сечений. Примером равномерного движения служит движение жидкости в цилиндрической трубе постоянного сечения. При отсутствии хотя бы одного из указанных условий движение будет неравномерным. Такое движение может быть в конически сходящейся или расходящейся трубе или в расширяющемся (сужающемся) канале.

Безнапорным называется такое движение, когда жидкость имеет свободную, т.е. открытую и находящуюся обычно под атмосферным давлением, поверхность. При отсутствии такой поверхности движение называют напорным. Примером безнапорного движения является движение воды в реке или канале, а также трубе, сечение которой не полностью заполнено жидкостью. При напорном движении сечение трубы полностью заполняется жидкостью.

Для характеристики движения потока жидкости введено понятие площади живого сечения, под которой понимают площадь сечения потока, перпендикулярную направлению движения.

К элементом живого сечения потока относятся площадь F, смоченный периметр П, гидравлический радиус R_г.

Площадь живого сечения F потоков может быть различной геометрической формы. Живое сечение может ограничиваться твердыми стенками полностью или частично, когда часть его соприкасается со свободной поверхностью жидкости.

Смоченный периметр П представляет собой сумму линейных размеров той части периметра поперечного сечения канала (трубы), которая смачивается жидкостью.

Гидравлический радиус R_г – отношение площади живого сечения к смоченному периметру

. (1.23)

Для жидкости, заключенной в круглую трубу:

(d – диаметр трубы; r – радиус трубы).

Следовательно, для круглого сечения потока гидравлический радиус численно равен половине геометрического радиуса окружности трубы или четверти его диаметра. При одинаковых площадях живого сечения круглая форма в сравнении с другими имеет наименьший периметр.

Гидравлический радиус является одним из важнейших понятий гидравлики. Вместо гидравлического радиуса в гидравлике иногда пользуются понятием гидравлического или эквивалентного диаметра d_экв, который представляет собой условный диаметр живого сечения потока любой геометрической формы, находящегося в гидравлически равных условиях с круглым сечением диаметром d:

. (1.24)

Количество жидкости, протекающее через живое сечение в единицу времени, носит название расхода жидкости. Количество жидкости может быть выражено в массовых или объемных единицах:

– массовый расход жидкости; (1.25)

– объемный расход жидкости. (1.26)

В уравнениях (1.25) и (1.26) w – средняя скорость потока w_ср в данном живом сечении, т.е. скорость, с которой должны были двигаться все частицы жидкости через рассматриваемое плоское сечение площадью F, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям этих частиц:

. (1.27)

Существуют два принципиально различных режима движения вязкой жидкости: ламинарный и турбулентный.

Ламинарный режим течения наблюдается при малых скоростях движения или большой вязкости жидкости. При этом частицы жидкости движутся в одном направлении параллельно друг другу, не перемешиваясь. По сечению трубопровода скорости частиц изменяются по параболическому закону (рис. 1.7, а). У стенки трубы скорость равна нулю, по оси – максимальная.

Турбулентный режим наблюдается при больших скоростях. Частицы жидкости при этом движутся беспорядочно по пересекающимся направлениям. В каждой точке потока происходят пульсации скорости относительно некоторой средней величины. Профиль распределения скоростей – более плоский по сравнению с ламинарным режимом (рис. 1.7, б).

Рисунок 1.7. – Распределение скоростей при ламинарном (а) и турбулентном (б) движении жидкости в трубе

Режим движения жидкости характеризуется безразмерным числом Рейнольдса Re, которое для трубы любого сечения равно

, (1.28)

где R_г – гидравлический радиус; w – средняя скорость движения жидкости; n — кинематический коэффициент вязкости; d_экв – эквивалентный диаметр.

Для трубы круглого сечения

(1.29)

(d – диаметр трубопровода; r и m –плотность и динамический коэффициент вязкости жидкости, соответственно).

Граница между ламинарным и турбулентным режимами движения жидкости определяется критическим числом Рейнольдса Re_кр. При Re Re_кр – турбулентное. Значения Re_кр могут колебаться в довольно широких пределах в зависимости от многих факторов: условий входа в трубу, шероховатости стенок трубы, рода и температуры жидкости и других условий. Причем Re при переходе от ламинарного к турбулентному движению больше, чем при обратном переходе. Опытным путем было установлено, что смена режимов течения жидкости в цилиндрических трубах круглого сечения происходит при Re_кр = 2300. Турбулентное движение становится вполне устойчивым только при Re ≥ 10000. При 2300

Видео:Основной закон гидростатикиСкачать

Уравнения гидростатики

Основное уравнение гидростатики, выражаемое часто в виде закона Паскаля, имеет ряд важных практических приложений; некоторые из них рассматриваются ниже.

Принцип сообщающихся сосудов и его использование. Пусть два от­крытых сообщающихся сосуда (рис. II-4, а) заполнены жидкостью плотностью р. Выберем произвольно плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно уравнению (II,18г), давление в данной точке

(II,18)

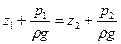
Если же считать точку А принадлежащей правому сосуду, то давление в ней

(z’ = z» = 0, так как плоскость 0-0 проходит через точку А).

При равновесии для каждой точки давление одинаково в любом на­правлении (в противном случае происходило бы перемещение жидкости). Следовательно

(II,19)

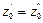
Аналогичный вывод может быть сделан для двух закрытых сообщаю­щихся сосудов, в которых давления над свободной поверхностью жид­кости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и попереч­ного сечения сосудов. Этот принцип используется, в частности, для измере­ния уровня жидкости в закрытых аппаратах с помощью водомерных стекол,

Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности r’ (левый сосуд) и r» (правый сосуд), то при проведении плоскости сравнения 0—0 через границу раздела жидко­стей (рис. II-4, б) аналогично предыдущему получим

(II,20)

(II,20a)

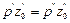
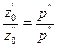
Отсюда следует, что в сообщающихся сосудах высоты уровней разно­родных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью r, но давления над уровнем жидкости в них неодинаковы и равны р’ (левый сосуд) и р» (правый сосуд), то

откуда разность уровней жидкости в сосудах

(II,21)

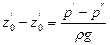
Уравнение (II,21) применяют при измерениях давлений или разностей давлений между различными точками с помощью дифференциальных U-образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных ап­паратах. Так, в непрерывно действующих сепараторах (рис. II-5) смесь жидкостей различной плотности (эмульсия) непрерывно поступает в ап­парат 1 по центральной трубе 2 и расслаивается в нем, причем более легкая жидкость плотностью r’ удаляется сверху через штуцер 3, а более тяжелая имеющая плотность r», — снизу через U-образный затвор 4.

Если при­нять, что уровень границы раздела фаз поддерживается на границе ци­линдрической и конической частей аппарата и провести через эту границу плоскость сравнения 0-0, то необходимая высота гидравлического затвора, согласно уравне­нию (II,20), составит

(II,20б)

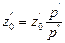
При этом допускается, что давление над жидкостью внутри аппарата и на выходе из затвора одинаково.

Пневматическое измерение количества жидкости в резервуарах. Для контроля за объемом жидкости в каком-либо резервуаре 1, например подземном (рис. II-6), в него помещают трубу 2, нижний конец которой доходит почти до днища резервуара. Давление над жидкостью в резервуаре равно р₀. По трубе 2 подают сжатый воздух или другой газ, постепенно повышая его давление, замеряемое манометром 3. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление р, фиксируемое манометром, перестанет воз­растать и будет равно, согласно уравнению (II,18г)

откуда уровень жидкости в резервуаре

(II,22)

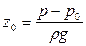
По величине z₀ и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

Гидростатические машины. На использовании основного уравнения гидростатики основа-на работа гидростатических машин, например гид­равлических прессов (рис. II-7), применяемых в химической промышленности для прессования и брикети-рования различных материа­лов. Если приложить относительно небольшое усилие к поршню 1, дви­жущемуся в цилиндре меньшего диаметра d₁, и создать давление р на поршень, то, согласно закону Паскаля, такое же давление р будет при­ходиться на поршень 2 в цилиндре большего диаметра d₂. При этом сила давления на поршень 1 составит

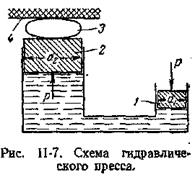
а сила давления на поршень 2

В результате поршень в цилиндре большего диаметра передаст силу давления, на столько большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, на сколько поперечное сечение цилиндра 2 больше, чем цилиндра 1. Таким способом с помощью сравнительно не­больших усилий осуществляют прессование материала 3, помещенного между поршнем 2 и неподвижной плитой 4.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех точках гори­зонтального дна сосуда одинаково, давление же на его боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление р на уровне дна сосуда (рис. II-3), как и для любой точки внутри жидкости, определяется уравнением (II,18г), но для всех точек дна величина (z₀ — z) представляет собой высоту жид­кости в сосуде. Обозначив последнюю через H, получим

(II,23)

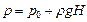
Таким образом, сила давления P на горизонтальное дно сосуда не зави­сит от формы сосуда и объема жидкости в нем. При данной плотности жидкости эта сила определяется лишь высотой столба жидкости Н и пло­щадью F дна сосуда:

Гидростатическое давление, жидкости на вертикальную стенку сосуда изменяется по высоте. Соответственно сила давления на стенку также раз­лична по высоте сосуда. Поэтому

где h — расстояние от верхнего уровня жидкости до центра тяжести смоченной пло­щади F стенки.

В уравнении (II,24а) выражение в скобках представляет собой гидро­статическое давление в центре тяжести смоченной площади стенки. По­этому сила давления на вертикальную стенку равна произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки.

Точка приложения равнодействующей Р сил давления на стенку называется центром давления. Эта точка расположена всегда ниже центра тяжести смоченной площади. Если давление р₀ передается жидкостью в одинаковой степени каждому элементу стенки, независимо от глубины его погружения, и, следовательно, равнодействующая сила этого давления приложена в центре, тяжести стенки, то давление столба жидкости на стенку тем больше, чем глубже расположен соответствующий ее элемент. В результате, в частности, для вертикальной прямоугольной стенки центр давления расположен на расстоянии 2/3 Н от верхнего уровня жидкости.

📸 Видео

Закон БернуллиСкачать

3.1. Основы гидростатики. ЛекцияСкачать

3.1 Основы гидростатики. ПрактикаСкачать

ОСНОВНЫЕ ЗАКОНЫ ГИДРОСТАТИКИСкачать

Закон ПаскаляСкачать

Закон БернуллиСкачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Следствие из основного уравнения гидравлики: закон ПаскаляСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Гидростатическое давлениеСкачать

Гидравлика лекция 2Скачать

Гидростатический парадокс или как Паскаль бочку разорвалСкачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Уравнение Бернулли гидравликаСкачать