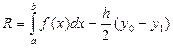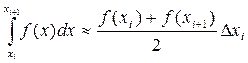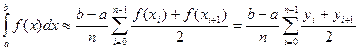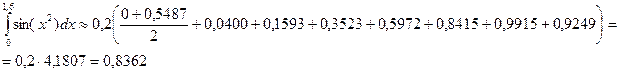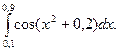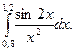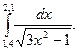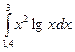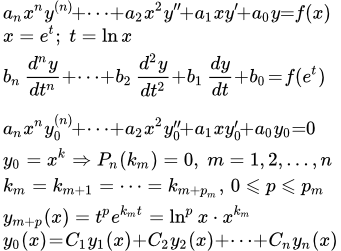Практическое занятие №25
«Численное интегрирование с помощью формул прямоугольников, трапеций, Симпсона.
Приближенное решение дифференциальных уравнений с помощью формул Эйлера»
1. Цель: Выработать навыки и умения по применению методов приближённого
интегрирования – формул прямоугольников, трапеций и Симпсона, в решении
приближенными методами дифференциальных уравнений
Пояснения к работе
2.1 Краткие теоретические сведения:
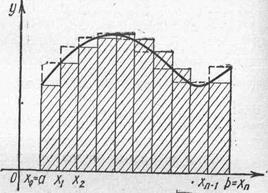
Формула прямоугольников
Известно, что не для всякой непрерывной функции ее первообразная выражается через элементарные функции. Кроме того, на практике сталкиваются с необходимостью вычислять интегралы от функций, заданных табличным или графическим способами, а так же интегралы от функций, первообразные которых выражаются через элементарные очень сложно, что требует большой вычислительной работы и с практической точки зрения нерационально. В этих случаях вычисление определенного интеграла по формуле Ньютона – Лейбница затруднительно, поэтому прибегают к различным методам приближенного интегрирования. Наиболее простым методом приближенного вычисления определенного интеграла является метод прямоугольников, основанный на непосредственном определении интеграла:
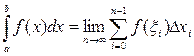
где 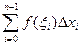
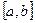
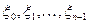
Вычисление определенного интеграла 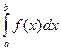
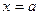
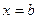
Для точности численного интегрирования нужно отрезок 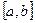

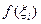
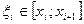
интеграла на отрезке 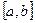
Практически удобно делить отрезок 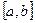
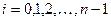
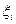
левыми 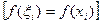
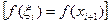
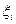
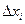
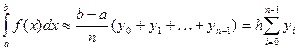
где 
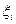
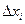

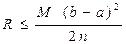
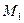
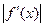
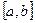
Пример 1. Используя формулу прямоугольников при 

Решение: разделим отрезок 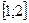
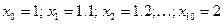

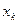 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 |
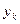 | 1.000 | 0.909 | 0.833 | 0.769 | 0.714 | 0.667 | 0.625 | 0.588 | 0.556 | 0.526 | 0.5 |
Тогда получим 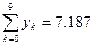
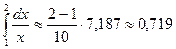
Оценим погрешность. Имеем 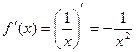
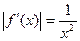
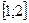
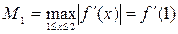

Так как допущенная погрешность влияет уже на второй знак после запятой, то третий знак следует округлить. Значит, 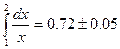
Лейбница, то получим 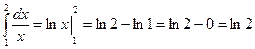
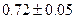

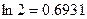
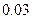
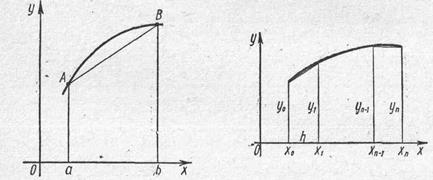
Формула трапеций
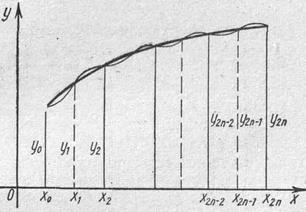
Приближенное значение определенного интеграла можно вычислить и иным способом.
Заменим на отрезке 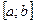
интеграла численно равным площади этой трапеции.
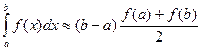
Это и есть формула трапеций для приближенного вычисления интеграла. Погрешность вычисления
для формулы трапеций оценивается так:
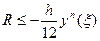
где точка 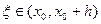
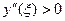
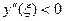
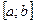
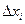
Для простоты вычислений удобно делить отрезок 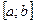
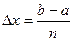
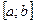
Эта формула называется общей формулой трапеций. Общую формулу трапеций можно переписать в более удобном виде:
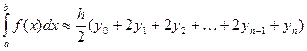

Пример 2.Вычислить интеграл 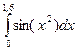
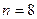
Решение: составим таблицу значений подынтегральной функции при 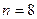
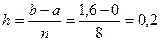
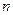 | 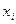 | 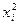  | 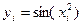 | 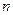 | 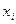 | 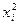 | 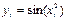 |
| 0,2 0,4 0,6 | 0,02 0,16 0,36 | 0,0000 0,0400 0,1593 0,3523 | 0, 1,0 1,2 1,4 1,6 | 0,64 1,0 1,44 1,96 2,56 | 0,5972 0,8415 0,9915 0,9249 0,5487 |
Используя формулу 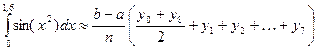
Находим:
Примечание. Если данный интеграл вычислить при 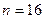
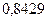
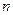
Формула Симпсона
Точность приближенного интегрирования заметно возрастает, если подынтегральную функцию 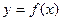
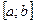
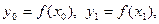
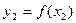
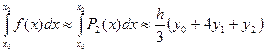
Соотношение (7) называется формулой Симпсона. Формула Симпсона обладает повышенной точностью и является точной не только для многочленов второй степени, но и третьей. Погрешность формулы Симпсона оценивается следующим образом:
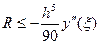
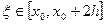
Для увеличения точности вычислений отрезок 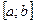
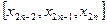
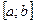
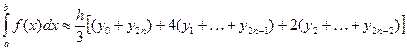
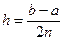
Соотношение (9) называется общей формулой Симпсона.
Пример 3. Вычислить по формуле Симпсона 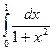
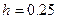
По формуле (9) имеем 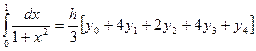
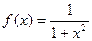
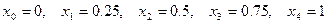
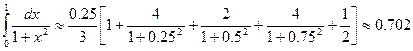
Приближенное решение обыкновенных дифференциальных уравнений. Метод Эйлера
Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка, разрешенное относительно производной:

Основная задача, связанная с этим уравнением, известна как задана Коши:найти решение уравнения (10) в виде функции у(х), удовлетворяющей начальному условию

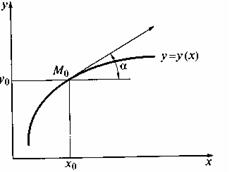
Геометрически это означает, что требуется найти интегральную кривую у = у(х), проходящую через
заданную точку M0(x0, .y0), при выполнении равенства (11) (см. рис.6). С численной точки зрения задача Коши выглядит следующим образом: требуется построить таблицу значений функции у=у(х), удовлетворяющей уравнению (10) и начальному условию (11) на отрезке [a;b]с некоторым шагом h. Обычно считается, что х0 = а, т.е. начальное условие задано в левом конце отрезка.
Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера.В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть дано уравнение (10) с начальным условием (11) (т.е. поставлена задача Коши). Решим вначале следующую задачу: найти простейшим способом приближенное значение решения в некоторой точке x1 = х0 + h, где h — достаточно малый шаг.
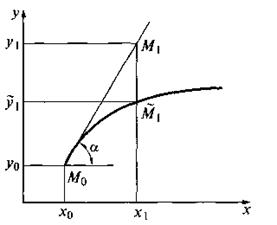
Заметим, что уравнение (10) совместно с начальным условием (11) задают направление касательной к искомой интегральной кривой в точке М0(х0, у0). Уравнение касательной имеет вид
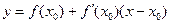
Двигаясь вдоль этой касательной (рис. 7), учитывая соотношения (10) и (12), получим приближенное значение решения в точке х1:
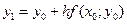
Располагая приближенным решением в точке М1 (х1,y1), можно повторить описанную ранее процедуру: построить прямую, проходящую через эту точку с угловым коэффициентом f (х1, y1) и по ней найти приближенное значение решения в точке х2 = х1 + h. Заметим, что в отличие от ситуации, изображенной на рис. 7, эта прямая не есть касательная к реальной интегральной кривой, поскольку точка M1, нам недоступна. Однако представляется интуитивно ясным, что если h достаточно мало, то получаемые приближения будут близки к точным значениям решения.
Продолжая эту идею, построим систему равноотстоящих точек
Получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом
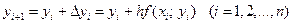
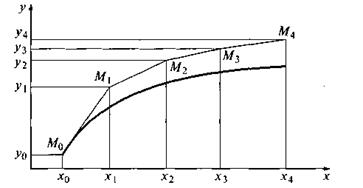
Геометрическая иллюстрация метода Эйлера приведена на рис. 8. Вместо интегральной кривой в реальности получается совокупность прямых (так называемая ломаная Эйлера).
Рис.8 Ломаная Эйлера
Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представитель семейства пошаговых методов.
Отметим, что оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага исходное значение у, в формуле (13) само является приближенным, т.е. погрешность на каждом следующем шаге систематически возрастает.
Наиболее используемым эмпирическим методом оценки точности как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).
Одна из принципиальных трудностей всех пошаговых методов численного решения дифференциальных уравнений состоит в возможности столкнуться с неустойчивостью метода. Оценка погрешности неявно предполагает, что ломаная приближенного решения (см. рис. 8) хотя и не совпадает с интегральной кривой, но качественно на нее похожа. Чаще всего это именно так, но иногда (например, при неудачном выборе шага h) приближенное решение может быть качественно непохожим на точное (например, точное монотонно убывает, а приближенное монотонно возрастает).
Для эмпирического контроля того, не имеет ли места неустойчивость, следует численно интегрировать уравнение с несколькими, значительно отличающимися, значениями шага h, сравнивая качественно поведение решений.
Пример 4.Применяя метод Эйлера, составить таблицу значений решения дифференциального уравнения 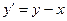
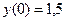
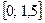
Для удобства вычислений составим таблицу.
1-й шаг: по начальным условиям заполним первую строку во 2-м и 3-м столбцах ;
2-й шаг: из уравнения 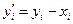
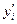
3-й шаг: содержимое столбца (4) умножаем на h (вычисляем 
записываем результат в столбец (5) этой же строки;
4-й шаг: к содержимом столбца (3) прибавляем содержимое столбца (5) этой же строки
(вычисляем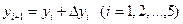
строки. Определяем хi+1 = xi + h и затем шаги 2-4 повторяем до тех пор, пока не будет пройден
весь отрезок 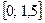
| i | xi | yi | 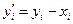 | 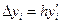 |
| (1) | (2) | (3) | (4) | (5) |
| 1,5000 | 1,5000 | 0,3750 | ||
| 0,25 | 1,8750 | 1,6250 | 0,4062 | |
| 0,50 | 2,2812 | 1,7812 | 0,4453 | |
| 0,75 | 2,7265 | 1,9765 | 0,4951 | |
| 1,00 | 3,2206 | 2,2206 | 0,5552 | |
| 1,25 | 3,7758 | 2,5258 | 0,6314 | |
| 1,50 | 4,4072 |
Пример 5. Решить методом Эйлера дифференциальное уравнение 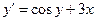
Решение: результаты вычислений с двумя знаками после запятой приведены в таблице:
| i | xi | yi | 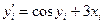 | 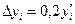 |
| (1) | (2) | (3) | (4) | (5) |
| 0,0 | 1,3 | 0,27 | 0,05 | |
| 0,2 | 1,35 | 0,82 | 0,16 | |
| 0,4 | 1,51 | 1,25 | 0,25 | |
| 0,6 | 1,76 | 1,61 | 0,32 | |
| 0,8 | 2,08 | 1,91 | 0,38 | |
| 1,0 | 2,46 |
Задание
Вариант 1
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 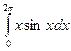
2. По формуле трапеций n=10 вычислить значение интеграла с тремя десятичными
знаками: 
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 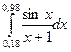
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
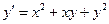
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 2
1.По формуле левых прямоугольников для n=12 вычислить значение интеграла: 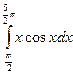
2.По формуле трапеций n=8 вычислить значение интеграла с тремя десятичными
знаками: 
3.По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками: 
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
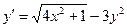
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 3
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2.По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными
знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
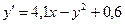
Сделайте ручную прикидку графика интегральной кривой на бумаге.
Вариант 4
1.По формуле правых прямоугольников для n=12 вычислить значение интеграла:
2. По формуле трапеций для n=10 вычислить значение интеграла с тремя десятичными знаками:
3. По формуле Симпсона для n=6 вычислить значение интеграла с тремя десятичными
знаками:
4. Применяя методом Эйлера, составить таблицу значений решения дифференциального уравнения
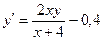
Сделайте ручную прикидку графика интегральной кривой на бумаге.
4. Контрольные вопросы:
1. Какие методы приближенного вычисления определенных интегралов вы знаете? Назовите
формулы для вычислений. Какой из них дает наиболее точный результат?
2. На чем основан метод Эйлера приближенно решения дифференциальных уравнений?
5. Содержание отчёта:
5.1 Наименование работы
5.4 Формулы для расчета
5.5 Необходимые расчеты. Анализ результатов расчетов
5.6 Выводы по работе
5.7 Ответы на контрольные вопросы
1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие — М.
Новая волна, 2005, ч.1, с.565-571;
2. Богомолов Н.В. «Практические занятия по математике» — Учебное пособие – М.:Высш. школа,
3. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Элементы численных методов: учебник для студ. сред.
проф. образования -М.: Издательский центр «Академия», 2007, с.152-184
- Дифференциальное уравнение Эйлера и методы его решения
- Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
- Решение однородного уравнения Эйлера
- Примеры
- Решение неоднородного уравнения Эйлера
- Пример
- Неоднородное уравнение Эйлера со специальной неоднородной частью
- Курсовая работа: Решение дифференциальных уравнений по методу Эйлера
- 💥 Видео
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Дифференциальное уравнение Эйлера и методы его решения
Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Видео:Метод ЭйлераСкачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Видео:Численное решение задачи Коши методом ЭйлераСкачать

Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Курсовая работа: Решение дифференциальных уравнений по методу Эйлера
| Название: Решение дифференциальных уравнений по методу Эйлера Раздел: Рефераты по математике Тип: курсовая работа Добавлен 20:43:28 26 декабря 2010 Похожие работы Просмотров: 1331 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |
 |





Получаем точку Nk / . В этой точке строим следующую касательную:
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой xк1 . Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
Эти формулы называются рекуррентными формулами метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции yк+1/2 в точках xк+1/2 , затем находят значение правой части уравнения (1) в средней точке
3. Блок-схема алгоритма
где A — начальное значение x, B — конечное значение x, F(x) — значение функции в точке xn , N — количество промежутков, st – выбор операции, C1,C2,C3 – константы для формул, nom — сохраняет номер используемой функции.
На рисунке представлена блок-схема процесса решения дифференциального уравнения методом Эйлера
Подсчитывая каждый раз новое значение уравнения F(x), получаем последовательность значений xn yn , n=1,2,…
По этим значениям строим график.
4. Описание программы
Программа весьма проста. В ней много предусмотрено моментов неправильного ввода данных, о которых программа предупреждает пользователя и сразу же просит повторно ввести данные.
С самого начала программа предоставляет пользователю меню выполняемых функций, которые выделяются при помощи стрелок ↑ и ↓ выбор клавишей Enter:
После запуска программы нужно выбрать Formyla -> Enter, эта опция позволит из предложенного списка формул выбрать одну, по которой компьютер будет производить расчет и строить график. Все предложенные формулы имеют номерацию; чтобы выбрать интересующий вас пример нажмите на цифру равную номеру примера, и сразу же появится новое окно, в котором сверху будет записан ваш пример. Также в окне будет этот же пример но с нулями на месте констант. Под примером будет высвечена большая буква С, это используется для ввода констант. Для этого вам нужно нажать номер константы, он появится, и после знака равно запишите чему она равна (вводятся целые и вещественные значения). По окончании набора нажать Enter. Операцию повторять пока не будут введены все числа. По окончании нажать Esc. После появится строчка «уточните границы изменения Х, от A= до B= » здесь нужно занести данные на каком промежутке абсциссы будет рассматриваться функция. Следующая строчка попросит ввести начальные данные y(A)=. Следующей строчкой будет вопрос: «сохранить данные в файле? Да/Нет» ответить на этот вопрос с помощью клавиш Д и Н (рус), после чего программа вернется в первоначальное меню. Если данные были сохранены (в папке с программой появляется файл form.txt), то в следующий раз чтобы не набирать снова выберите в меню опцию Formyla -> Open in fails и на экране появятся введенные данные с пометкой снизу, сообщая что данные были прочитаны из файла.
Следующая опция Reshenie. После нажатия в окне просят ввести N(целое число) – число промежутков, на которые разделится рассматриваемый участок (ось ОХ). После появится таблица рассчитанных данных (номер точки, значение абсциссы, значение ординаты). При нажатии любой клавиши произойдет переход в меню.
Graphic эта опция позволяет визуально видеть решение, а так же на этом графике прописываются все данные: начальная формула, шаг и промежуток построения графика, масштаб, данные об его изменении(клавишами +(увеличить) и -(уменьшить), а также возможность определить точное значение функции в любой точке.
Опция Exit применяется для выхода из программы.
Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать дифференциальные уравнения по методу Эйлера, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности.
Данная программа решает заданную пользователем дифференциальное уравнение за минимальный промежуток времени. При этом пользователю предоставляется возможность визуально оценить решение, рассматривая график полученного решения.
К достоинствам программы можно отнести также удобный пользовательский интерфейс, возможность ввода пользовательских дифференциальных уравнений, а также давольно высокая стабильность работы. Однако имеются и некоторые недостатки. К недостаткам программы можно отнести: критичность к вводимым пользователем урававней, отсутствие обработки исключительных событий. Это, естественно, ограничивает возможности программы.
Список использованной литературы
1. Д. Мак-Кракен, У. Дорн. Численные методы и программирование на фортране. –М.: Мир,1977.-389,396-408 с.
2. А.А. Самарский. Введение в численные методы. – М.:Наука,1987.-176 с.
3. Алгоритмы вычислительной математики: Лабораторный практикум по курсу «Программирование» для студентов 1 — 2-го курсов всех специальностей БГУИР/А.К. Синицын, А.А. Навроцкий.- Мн.: БГУИР, 2002.- 65-69 с.
4. ГОСТ 2.105-95. Общие требования к текстовым документам.
5. ГОСТ 7.32-91. Система стандартов по информации, библиотечному и издательскому делу. Отчет о НИР. Структура и правила оформления.
Приложение 1. Текст программы.
void formyl(int p)
if(p==1) printf(«n 1. C1*y’ = C2*y + C3*x + C4*x*y»);
else if(p==2) printf(«n 2. y’/(C1-100) = C2*y + C3*x + (C4+x)*y»);
else if(p==3) printf(«n 3. pow(e,C1)*y’ = C2*y + C3*cos(x) + (C4+x+y)»);
else if(p==4) printf(«n 4. C1*sin(x)*y’ = e*C2*y + C3*arcsin(x) + C4*y/x»);
else if(p==5) printf(«n 5. C1*y’ = sin(C2)*y + tg(C3*x) + C4*ln(x)*y»);
else if(p==6) printf(«n 6. C1*y’ = y*C2 + C3*sin(x) + C4*cos(x)*y»);
else if(p==7) printf(«n 7. (C1+C2+C3+C4)*y’ = C2*y + (C3-x) + lg(C4*x)*y»);
else if(p==8) printf(«n 8. y’/C1 = y/C2 + C3*sin(x) + C4*x*y»);
else if(p==9) printf(«n 9. sin(C1)*y’ = C2*y + |C3|*x + x*y/C4»);
void formyl2(int p,double C1,double C2,double C3,double C4)
else if(p==2) printf(«y’/(%.2f-100)=%.2f*y+%.2f*x+(%.2f+x)*y»,C1,C2,C3,C4);else if(p==3) printf(«pow(e,%.2f)*y’=%.2f*y+%.2f*cos(x)+(%.2f+x+y)»,C1,C2,C3,C4);
else if(p==4) printf(«%.2f*sin(x)*y’=e*%.2f*y+%.2f*arcsin(x)+%.2f*y/x»,C1,C2,C3,C4);
else if(p==5) printf(«%.2f*y’=sin(%.2f)*y+tg(%.2f*x)+%.2f*ln(x)*y»,C1,C2,C3,C4);
else if(p==6) printf(«%.2f*y’=y*%.2f+%.2f*sin(x)+%.2f*cos(x)*y»,C1,C2,C3,C4);
else if(p==8) printf(«y’/%.2f=y/%.2f+%.2f*sin(x)+%.2f*x*y»,C1,C2,C3,C4);
else if(p==9) printf(«sin(%.2f)*y’=%.2f*y+|%.2f|*x+x*y/%.2f»,C1,C2,C3,C4);
double formyl3(int p,double h,double x,double y,double C1,double C2,double C3,double C4)
else if(p==2) Y=h*(C1-100)*(y*C2+C3*x+(C4+x)*y)+y;
else if(p==3) Y=h*(C2*y+C3*cos(x)+C4+x+y)/exp(C1)+y;
else if(p==4) Y=h*(exp(1)*C2*y+C3*asin(x)+C4*y/x)/(C1*sin(x))+y;
else if(p==5) Y=h*(sin(C2)*y+tan(C3*x)+C4*log10(x)*y)/C1+y;
else if(p==6) Y=h*(y*C2+C3*sin(x)+C4*cos(x)*y)/C1+y;
else if(p==7) Y=h*(C2*y+(C3-x)+log10(C4*x)*y)/(C1+C2+C3+C4)+y;
else if(p==8) Y=h*(y/C2+C3*sin(x)+C4*x*y)*C1+y;
else if(p==9) Y=h*(C2*y+abs(C3)*x+x*y/C4)/sin(C1)+y;
int vv=0,vv1=0; // руководит операциями
int N=0,W; // кол промежутков
int i,j,k; // используются во всех «for»
int nom; // номер примера
int st=4,vst=0; // строчка в меню
double C1,C2,C3,C4; // константы
double M; // масштаб
double xtoch,ytoch; // считает y(x) по графику
double A=0,B=0,ii,jj,kk; // пределы интегрирования
double x[102],y[102]; // главные переменные x,y
int g_driver=9,g_mode=2, g_error;
printf(«n error=%d, reason=%sn», g_error, grapherrormsg(g_error));
💥 Видео
Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Численные методы решения ДУ: метод ЭйлераСкачать

Метод Эйлера. Решение систем ДУСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Системы дифференциальных уравнений.Метод исключения.Метод Эйлера.Скачать