Практическая работа уравнение касательной к графику функции

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Тестовые задания по теме: «Касательная к графику функции»

Разделы: Математика

При изучении темы “Касательная к графику функции” можно выделить 5 типов задач.

I. Задачи на составление уравнения касательной к графику функции в точке, принадлежащей графику

Обучение решению задач на касательную осуществляется при помощи алгоритма.

Уравнение касательной к графику функции y=f(x) в точке х: y = f(х) + f ‘(х)(x – х)

Алгоритм составления уравнения касательной к графику функции y = f(x):

1. Обозначить х абсциссу точки касания.

2. Найти f(х)

3. Найти f ‘(x) и f ‘(х) 4. Подставить найденные числа х, f(х), f ‘(х) в общее уравнение касательной

Задача. Составьте уравнение касательной к графику функции в точке с абсциссой х=3.

1. х = 3 – абсцисса точки касания.

3. f ‘(x) = x 2 – 4, f ‘(3) = 5. 4.Подставив в уравнение касательной значения х=3, f(х)=-2, f ‘(х)=5, получим y = – 2 + 5(x – 3), т.е. y = 5x – 17. Это и есть искомое уравнение касательной. Ответ: y = 5x-17.

Найти уравнение касательной к графику функции f(x) в точке с абсциссой х.

1. f(x)=-x-4x+2, х=-1.	1) y=-2x-3;	2) y=2x-1;	3) y=-2x+3;	4) y=2x+3.
2. f(x)=-x+6x+8, х=-2.	1) y=2x-6;	2 )y=10x+12;	3) y=4x+8;	4) y=-10x+8.
3. f(x)=x+5x+5, х=-1.	1) y=7x+8;	2) y=8x+7;	3) y=9x+8;	4) y=8x+6.
4. f(x)=2cosx, х=	1) y=	2) y=	3) y=	4) y=
5. f(x)=tgx, х= 1) y=x;	2) y=x+	3) y=x-	4) y=x-1.
6. f(x)=1-sin2x, х=0.	1) y=1-2x;	2) y=2x;	3) y = -2x;	4) y=2x+1.
7. f(x)= х=-2.	1) y = -x+1; 2) y = x+1;	3) y = -x-1;	4) y = -x-2.

8. Уравнение касательной, проведённой к графику функции y=lnx в точке его пересечения с осью абсцисс, имеет вид. 1) y = 2x-2; 2) y = x-1; 3) y = x+1; 4) y = x.

9. Уравнение касательной, проведённой к графику функции y=e-1 в точке его пересечения с осью абсцисс, имеет вид. 1) y = 2x; 2) y = 3x-1; 3) y = x-1; 4) y = x.

10. Уравнение касательной, проведённой к графику функции y=sin(x-)+1 в точке его пересечения с осью ординат, имеет вид. 1) y = x+1; 2) y = x-1; 3) y =- x-1; 4) y =1- x.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	3	2	2	2	3	1	3	2	4	4

II. Проведение касательной параллельно заданной прямой

Задача 1. В каких точках касательные к кривой у=— х— х+1 параллельны прямой y=2x-1?

Решение. Так как касательные параллельны прямой у=2х-1 то их угловые коэффициенты совпадают. Т. е. угловой коэффициент касательной в этой точке есть к = 2 .

Находим у’ = х-2х-1; к= у'(х)= х-2х-1=2.

Решив уравнение х-2х-1=2; х-2х-3=0, получим (х)=3, (х)=-1, откуда (у)= -2, (у)= . Итак, искомыми точками касания являются А(3;-2) и В(-1;)

Ответ: (3;-2) и (-1;).

Задача 2. Найти абсциссу точки, в которой касательная к графику функции f(x) = 2x-lnx, параллельна прямой у = х.

Решение. Пусть х— абсцисса точки касания. Угловой коэффициент касательной в этой точке есть к=1. Находим f ‘(x)=2-. К= f ‘ (х)=2-=1.

Решив уравнение 2-=1, получим х=1.

Найти абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у(х).

1. f(x)= х+е, у(х)= -х.	1) —; 2) 0; 3) ; 4) 1.
2. f(x)=2+х, у(х)= 2х.	1) 1; 2) 4; 3) 0; 4) .
3. f(x)=х-5х, у(х)= -х.	1) -2; 2) 3; 3) -3; 4) 2.
4. f(x)=2lnх-x, у(х)= 0.	1) -2; 2) 0; 3) 2; 4) 1.
5. f(x)=-х-е, у(х)= 4-2х.	1) 3; 2) 2; 3) 0; 4) –2.

6. Найти сумму абсцисс точек, в которых касательные к графику функции у=х— 3х+1 параллельны оси абсцисс. 1) 0; 2) 2; 3) 1; 4) –2.

7. Найти сумму абсцисс точек в которых касательные к кривой у= параллельны прямой у=х+5. 1) –2; 2) 4; 3) 2; 4) –4.

8. К графику функции у = проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х= -1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции. 1) –2; 2) 2; 3) 1; 4) –3.

9. К графику функции у =- проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х= 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции. 1) –1; 2) 5; 3) 2; 4) –3.

10. На графике функции у = х (х-4) указать точки, в которых касательные параллельны оси абсцисс. Найти сумму абсцисс данных точек. 1) 5; 2) 4; 3) 3; 4) – 27.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	1	4	2	2	1	4	3	2	1

III. Задачи на касательную, связанные с ее угловым коэффициентом

Задача 1. К графику функции f(x) = 3x+5x-15 в точке с абсциссой x= проведена касательная. Найти тангенс угла наклона касательной к оси Ох.

f'(x) является угловым коэффициентом касательной к графику функции у =f(x) в точке x. Угловой коэффициент прямой равен тангенсу угла, образованного этой прямой с положительным направлением оси Ох.

k= f ‘(x)=tg, где x— абсцисса точки касания, а — угол наклона касательной к оси Ох.

f ‘(x)= f ‘()=6. tg=6.

Задача 2. Напишите уравнение касательной к графику функции f(x) = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0.

Решение. f ‘(x)= x-3. Из условия f ‘(x) = tg 45° найдем x: x – 3 = 1, x= 4.

1. x= 4 – абсцисса точки касания.

2. f(4) = 8 – 12 + 1 = – 3.

4. y = – 3 + 1(x – 4). y = x – 7 – уравнение касательной

Задача 3. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=xlnx в точке x=1.

Решение. k= f'(x)=tg.

Находим f ‘(x)= 2xlnx+x=2xlnx+x=x(2lnx+1).

При x=1 получим f ‘(1)=1, откуда tg=1 и, значит, =.

Ответ: .

К графику функции f(x) в точке с абсциссой x проведена касательная. Найти тангенс угла наклона касательной к оси Ох если:

1. f(x)= 2+x-2x, x=1.	1) -1; 2) –7; 3) 3; 4) 0.
2. f(x)= , x=8.	1) 1; 2) 32; 3) 8; 4) 16.
3. f(x)= 5x-3x-7, x=-1.	1) 21; 2) 14; 3) 9; 4) -21.
4. f(x)= 3x-2lnx, x=2.	1) 10; 2) 8; 3) 11; 4) 11,5.
5. f(x)= -x+14, x=1.	1) -51; 2) –65; 3) 63; 4) 77.

Найти угловой коэффициент касательной проведённой к графику функции f(x) в точке x

6. f(x)=e-x, x=1.	1) e-2; 2) –1; 3) e-1; 4) –2.
7. f(x)=2sinx+2, x=0.	1) -2; 2) 0; 3) 4; 4) 2.
8. f(x)=4cosx-1, x=.	1) 4; 2) 2; 3) -2; 4) 1.
9. f(x)=2+3, x=4.	1) 3,5; 2) 0,5; 3) 7; 4) 2,5.

10. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=3lnx — x, в точке x=1. 1) 2) 3) arctg2; 4)

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	3	1	3	2	1	4	3	2	4

IV. Нахождение касательной проходящей через точку, внешнюю по отношению к заданному графику

Задача 1. Составить уравнения касательных к кривой y = x— 4x+3, проходящих через точку М(2;-5).

При х =2, находим у = 4-8+3=-1-5, то есть точка М не лежит на кривой y = x-4x+3 и не является точкой касания.

Пусть (х) – точка касания.

у ‘ =2х-4, k = 2x— 4. Составим уравнение касательной, проходящей через точку М:

у=-5-(2х-4)(2-х). Поскольку точка (х) лежит на кривой, получим y = x-4x+3.

Решим уравнение x-4x+3 = -5-(2х-4)(2-х);

x-4x+3=2x-8x+3, x— 4x=0, (х)=0, (х)= 4.

Таким образом, получили две точки касания А(0;3) и В(4;3). Итак, существуют две касательные к данной кривой; одна из них имеет угловой коэффициент k= -4 (при х=0) и уравнение у = -4х+3, а другая – угловой коэффициент k=4 (при х=4) и уравнение у=4х-13.

Ответ: у =-4х+3, у = 4х-13.

Через точку М(х;у) проведены две касательные к графику функции f(x). Найти сумму абсцисс точек касания.

1. f(x)=4х-8х-2, М(3;-90).	1) 4; 2) 6; 3) 5; 4) 3.
2. f(x)=7х-2х-5, М(2;-93).	1) 4; 2) 6; 3) 5; 4) 3.
3. f(x)=6х-4х-1, М(1;-23).	1) 1; 2) 5; 3) 2; 4) 3.
4. f(x)=х-8х-2, М(1,5;-54).	1) 2; 2) 4; 3) 5; 4) 3.
5. f(x)=х-9х-5, М(-1,5;4,5).	1) -2; 2) -5; 3) 2; 4) — 3.
6. f(x)=7х-7х-1, М(2;-50).	1) 4; 2) 6; 3) 5; 4) 3.

7. Напишите уравнение касательной к графику функции f(x)= х— 4х + 5, если эта касательная проходит через точку А(0;4) и абсцисса точки касания положительна.

1) у = 2х+4; 2) у = -2х+4; 3) у = -4х+4; 4) у = 4х-3.

8. Напишите уравнение касательной к графику функции f(x)= х+ 3х + 5, если эта касательная проходит через точку А(0;1) и абсцисса точки касания отрицательна.

1) у = 2х+1; 2) у = х+1; 3) у = -х+1; 4) у = -2х-5.

9. Напишите уравнения касательных к графику функции f(x)= -0,5 х+3, если эта касательные проходят через точку на оси Оу и образуют между собой угол 90 o ?.

1) у = х+3,5 и у = х-3,5 ; 2) у = -х+3,5 и у = х+3,5; 3) у = -х+4 и у =х+4; 4) у = -х+3 и у =х+3.

10. Через точку В(-2;3) проходят касательные к графику функции у=. Найти уравнения этих касательных.

1) у = 2х+2 и у = -22х+2; 2) у =-х+3 и у = х-3; 3)у =-0,5х+2 и у =х+4; 4)у =-0,5х+2 и у =-0,1х+2,8.

Ответы к упражнениям

Задание	1	2	3	4	5	6	7	8	9	10
Номер ответа	2	1	3	4	4	1	2	4	2	4

V. Нестандартные задачи, связанные с касательной

1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3. Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x₀ = 1, проходит через точку M(2; 3)? Ответ: a = 0,5.

3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2? Ответ: p₁ = – 10, p₂ = 2.

4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16). Ответ: A(2; – 2), B(– 4; 52).

5. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0. Ответ: M(2; 3).

6. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж. Ответ: y = 2x – 4.

7. На параболе y = x 2 взяты две точки с абсциссами x₁ = 1, x₂ = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.

Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.

8. Найдите угол между касательными к графику функции y = x 3 – 4x 2 + 3x + 1, проведенными в точках с абсциссами 0 и 1. Ответ: = 45°.

9. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5. Ответ: y = – 3x и y = x.

10. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.

Ответ: ₁ = arctg 6, ₂ = arctg (– 6).

11. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N. Ответ: K(1; – 9).

12. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15? Ответ: – 1; 31.

13. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.

14. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x₀ = 2, проходит через точку M(1; 8)?

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Практическое занятие «Касательная к графику функции» (для студентов СПО)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практическая работа №15 (естественно-научный профиль)

Тема: «Касательная к графику функции»

Цели: научиться находить угловой коэффициент касательной к графику функции в заданной точке; составлять уравнения касательных к графику функции по заданным условиям.

Краткая теоретическая справка.

Строгое определение касательной:

Касательная к графику функции f , дифференцируемой в точке x _о , — это прямая, проходящая через точку ( x _о ; f ( x _о )) и имеющая угловой коэффициент f ′( x _о ).

Угловой коэффициент имеет прямая вида y = kx + b . Коэффициент k и является угловым коэффициентом этой прямой.

Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:

Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой.
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).

Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).

Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).

Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c , где c – некоторое действительное число (рис.4).

Порядок выполнения работы.

Внимательно изучите теоретическую справку по теме.

Решите следующие задания.

Пример1. Найдем уравнение касательной к графику функции f ( x ) = x 3 – 2 x 2 + 1 в точке с абсциссой 2.

f ( x _о ) = f (2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Находим f ′( x ). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2 х , а х 3 = 3 х 2 . Значит:

3) Итак, у нас есть все необходимые данные: x _о = 2, f ( x _о ) = 1, f ′( x _о ) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

Пример 2. На рисунке изображены график функции y = f ( x ) и касательная к нему в точке с абcцисcой x ₀ . Найдите значение производной функции в точке x ₀ .

Значение производной функции y = f ( x ) в точке x ₀ равно тангенсу угла между касательной и положительным направлением оси ОХ. Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами А и В — эти точки выделены на касательной:

Проведем через точку А прямую параллельно оси ОХ, а через точку В — параллельно оси OY. Получим прямоугольный треугольник ABC. Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Длины катетов считаем по количеству клеточек

Пример 3. Найти угловой коэффициент касательной, проведенной к графику функции

в точке с абсциссой х0=1.

Тогда при x ₀ =1 значение производной равно

Отсюда получаем, что угловой коэффициент касательной в точке с абсциссой х ₀ =1 равен

Пример 4. Прямая y = 8 x -5 параллельна касательной к графику функции y = x 2 +7 x +7 . Найдите абсциссу точки касания.

Решение. Условием параллельности двух прямых является равенство их угловых коэффициентов, следовательно k =8 . Угловой коэффициент касательной – это есть значение производной функции в точке x ₀ . f ´( x ₀ ) = 2 x ₀ +7 =8, 2 x ₀ = -1, x ₀ = -0,5.

Выполните самостоятельную работу по вариантам.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Практическая работа по математике по теме: «Касательная к графику функции»

Инструкционная карта по выполнению практической работы по теме: «Касательная к графику функции».

Просмотр содержимого документа
«Практическая работа по математике по теме: «Касательная к графику функции»»

Тема: Касательная к графику функции.

— познакомиться с понятием касательной к графику функции, геометрическим смыслом касательной, формулой уравнения касательной;

— научиться проводить касательные к графику функции в данной точке, выводить уравнение касательной к данной функции в данной точке.

Норма времени: 2 часа

Оборудование: инструкционная карта

1. Познакомьтесь с основными вопросами темы и рассмотрите пример:

Прямую, проходящую через точку (х₀;f(x₀)), с отрезком которой практически сливается график функции f при значениях х, близких к х₀, называют касательной к графику функции f в точке (х₀;f(x₀)).

Геометрический смысл производной: Существование производной функции f в точке х₀ эквивалентно существованию (невертикальной) касательной в точке (х₀;f(x₀)) графика, при этом угловой коэффициент касательной равен

Касательная к графику дифференцируемой в точке х₀ функции f – это прямая, проходящая через точку (х₀;f(x₀)) и имеющая угловой коэффициент

Выведем уравнение касательной к графику функции f в точке А(х 0;f(x0)).

Уравнение прямой с угловым коэффициентом f ‘(x0)
имеет вид: y=f ‘(x0)х+b (y=kx+b-уравнение прямой, к=f ‘(x0)).

Так как касательная проходит через точку А:
f (x0)=f ‘(x0)х+b, откуда b=f(x0)-f ‘(x0)х0.

Таким образом уравнение касательной таково:
y=f ‘(x0)х-f ‘(x0)х0+f (x0)
или
y=f ‘(x0)х-f ‘(x0)(х-х0)

Найдём уравнение касательной к графику функции f(x)=x3–2×2+1 в точке с абсциссой х0

В этом примере х0=2,

f(x0)= f(2)=23 -2 22 +1=1,

f ‘(x0)= f ‘(2)=322 -4 2 =4,

Подставляя числа в уравнение касательной, получаем уравнение:

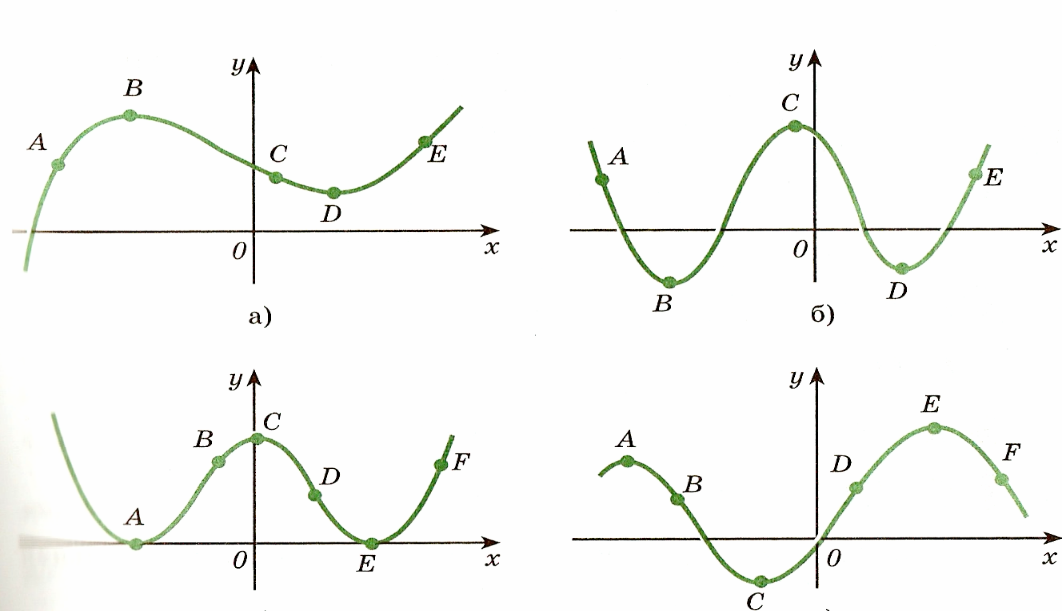
2. Проведите касательные к графикам в данных точках:

3. Выполните задание: Напишите уравнение касательной к графику функции f в точке с абсциссой х₀

1) f (х) = 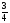, х₀=1 2) f (х) = х 2 +1, х₀ = -3

3) f (х) = х 3 + 1, х₀ = 2 4) f (х) = х 3 + 1, х₀ =2

5) f (х) = х 2 – 2х, х₀ = -2

1) f (х) = 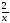, х₀ = -1 2) f (х) = 2х 2 — 1, х₀ = -2

3) f (х) = х 3 – 1, х₀ = 1 4) f (х) = — х 2 + 1, х₀ = -3

📺 Видео

Касательная к графику функции в точке. 10 класс.Скачать

Уравнение касательнойСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Уравнение касательной к графику функции в заданной точкеСкачать

Уравнение касательной к графику функции | Алгебра 10 класс #45 | ИнфоурокСкачать

Производная: касательная к графику.Скачать

Уравнение касательной к графику функции. Алгебра 10 классСкачать

Как составить уравнение касательной и нормали к графику функцииСкачать

Уравнение касательной к графику функции в задачах. Часть 1. Алгебра 10 классСкачать

Алгебра и начала анализа. 10 класс. Уравнение касательной к графику функции /01.02.2021/Скачать

Как написать уравнения касательной и нормали | МатематикаСкачать

Уравнение касательной к графику функции в задачах. Часть 5. Алгебра 10 классСкачать

Геометрический смысл производной. Уравнение касательнойСкачать

Уравнение касательной к графику функции в задачах. Часть 4. Алгебра 10 классСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Уравнение касательной к графику функцииСкачать

Касательная к графику функции. Простое объяснение формулыСкачать