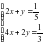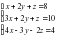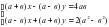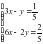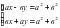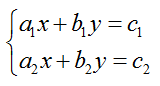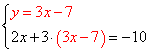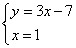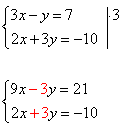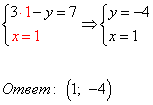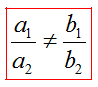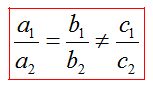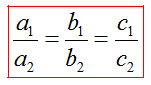Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера. Два варианта практических работ и методические рекомендации для решения систем линейных уравнений по формулам Крамера.
- Просмотр содержимого документа «Практическая работа по теме: «Решение систем линейных уравнений разными способами» и методичекие рекомендации для выполнения работы»
- Практическая работа: «Решение систем линейных уравнений различными способами»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Решение систем уравнений. план-конспект занятия по алгебре (10, 11 класс)
- Скачать:
- Предварительный просмотр:
- 🔥 Видео
Просмотр содержимого документа
«Практическая работа по теме: «Решение систем линейных уравнений разными способами» и методичекие рекомендации для выполнения работы»
Краевое государственное образовательное учреждение среднего профессионального образования «Хабаровский судостроительный колледж»
Специальность: 15.02.08 «Технология машиностроения»
Дисциплина: ЕН.01. «Математика», курс -1
Преподаватель — Михайлова М.Б.
Тема занятия: «Практическая работа: «Решение систем линейных уравнений»
Практическая работа по теме:
«Решение систем линейных уравнений»
Цель: формирование умений решать системы линейных уравнений разными способами: способом подстановки, способом алгебраического сложения, графическим способом и по формулам Крамера.
Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:
а) 
б) 
Решите систему уравнений по формулам Крамера:
Решите систему уравнений по формулам Крамера:
4. При каком значении а система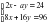 
имеет бесконечно много решений?
Решите систему уравнений способами алгебраического сложения, подстановки, графическим и по формулам Крамера:
а) 
б) 
Решите систему уравнений по формулам Крамера:
Решите систему уравнений по формулам Крамера:
При каком значении а система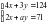 
не имеет решений?
Методические рекомендации для выполнения
практической работы по теме:
«Решение систем линейных уравнений»
Системы линейных уравнений
Решение системы линейных уравнений способом подстановки
Решение системы линейных уравнений способом сложения
Графическое решение системы линейных уравнений
График линейной функции
1. Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
Система уравнений такого вида, где a, b, c – числа, а x, y — переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
2. Решение системы линейных уравнений способом подстановки
Рассмотрим пример 
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.
3. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 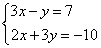методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
4. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
Ответ: (1; -4).
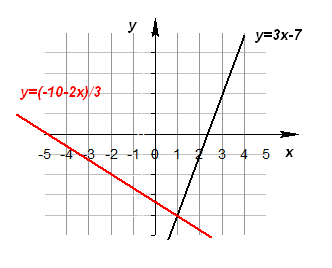
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система (1)
1) Если , то система (1) имеет единственное решение.
2) Если ,, то система (1) решений не имеет.
В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.
.
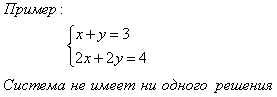
3) Если , то система (1) имеет бесконечное множество решений.
В этом случае прямые совпадают друг с другом.
.
II.Решение систем линейных уравнений по формулам Крамера
Система двух линейных уравнений с двумя переменными
Определитель системы уравнений.
Система трех линейных уравнений с тремя переменными
1.Решение систем линейных уравнений по формулам Крамера
Габриель Крамер (1704–1752) швейцарский математик.
Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, то есть ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель системы не равнялся .
Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
2.Система из двух уравнений с двумя неизвестными
решается с помощью формул Крамера:
При решении системы возможны три случая:
1. Определитель системы . Тогда система имеет единственное решение, определяемое формулами Крамера.
2. Определитель системы . Если при этом хотя бы один из определителей и не равен нулю, то система не имеет решений.
3. Если , и , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
П р и м е р 1. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители ,
Система имеет единственное решение
П р и м е р 2. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители , . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
Ответ: нет решений.
П р и м е р 3. Решить систему уравнений
Решение. Вычислим определитель системы , и дополнительные определители .
Так как , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на ).
Система сводится к одному уравнению и имеет бесчисленное множество решений, каждое из которых вычисляется по формуле: , где числовые значения задаются произвольно и вычисляются соответствующие значения .
Ответ: – общее решение данной системы, а решения – частные.
3.Система из трех уравнений с тремя неизвестными
При решении системы из трех уравнений с тремя неизвестными возможны три случая:
1. Определитель системы . Система имеет единственное решение, определяемое формулами Крамера ,
2. Определитель системы равен нулю, . Если при этом хотя бы один из определителей , не равен нулю, то система несовместна, решений не имеет.
3. Если и , то система имеет бесчисленное множество решений.
П р и м е р 4. Решить систему уравнений
Решение. Вычислим определитель системы и дополнительные определители
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать
Практическая работа: «Решение систем линейных уравнений различными способами»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка
а) 
в)
б)
Перечислите все известные вам способы решения систем линейных уравнений.
Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка. Сделать проверку.
а) 
в)
б)
2 . Запишите в общем виде систему из двух линейных уравнений и соответственно формулы Крамера к этой системе. В каком случае систему нельзя решать методом Крамера?
3 .Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка. Сделать проверку.
а) 
в)
б)
Поясните, в чём состоит суть метода Гаусса для решения систем линейных уравнений
Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка. Сделать проверку.
а) 
в)
б)
Поясните, в чём состоит суть графического метода для решения систем линейных уравнений.
Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка. Сделать проверку.
а) 
в)
б)
Что такое определитель второго и третьего порядка. Где используется понятие определителя второго порядка, третьего порядка?
Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Практическая работа №2
«Решение систем линейных уравнений различными способами»
Найти определители второго и третьего порядка
а) 
в)
б)
Поясните, в чём состоит суть метода сложения для решения систем двух линейных уравнений с двумя неизвестными.
Решить систему двух линейных уравнений всеми изученными методами ( подстановка, графический, сложения, Крамера):
а) 
б) 
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 575 831 материал в базе
Материал подходит для УМК
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
§ 59. Системы уравнений
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 29.09.2018
- 610
- 15
- 27.09.2018
- 480
- 1
- 27.09.2018
- 305
- 0
- 26.09.2018
- 148
- 1
- 26.09.2018
- 176
- 1
- 26.09.2018
- 303
- 4
- 26.09.2018
- 348
- 0
- 25.09.2018
- 594
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 29.09.2018 859
- DOCX 101 кбайт
- 7 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Сапожникова Галина Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 28494
- Всего материалов: 27
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Решение систем уравнений методом подстановкиСкачать
Решение систем уравнений.
план-конспект занятия по алгебре (10, 11 класс)
Практическая работа «Решение систем уравнений»
Видео:СИСТЕМА УРАВНЕНИЙ различные способы решения 9 10 класс алгебраСкачать
Скачать:
| Вложение | Размер |
|---|---|
| 96_reshenie_sistem_uravneniy.docx | 34.26 КБ |
Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Предварительный просмотр:
Тема: Решение систем уравнений.
— — закрепить основные приемы решения систем уравнений
Просмотрите видеоурок по ссылке:
Решить систему уравнений
Решим способом подстановки:
; 
; 
; 
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
1. Что значит решить систему уравнений?
2. Объясните алгоритм решения систем уравнений способом подстановки.
🔥 Видео
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Решение систем уравнений второго порядка. Практическая часть. 8 класс.Скачать
Матричный метод решения систем уравненийСкачать
Решение систем уравнений методом сложенияСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать
6 способов в одном видеоСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Решение систем уравнений методом сложенияСкачать
Решение системы уравнений методом ГауссаСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать
Решение систем уравнений второго порядка. 8 класс.Скачать
Решение систем уравнений. Методом подстановки. Выразить YСкачать
