- Просмотр содержимого документа «Практическая работа по теме: «Решение показательных уравнений и неравенств»»
- Решение задач по теме «Показательные функции, уравнения и неравенства»
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- 📺 Видео
Просмотр содержимого документа
«Практическая работа по теме: «Решение показательных уравнений и неравенств»»
Практическая работа №3
Тема: «Решение показательных уравнений и неравенств»
Цель: научиться применять свойства показательной функции для решения показательных уравнений и неравенств, закрепить знания и умения по применению методов решения показательных уравнений и неравенств для решения практических задач.
Основные теоретические положения
Определение. Уравнение вида 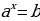
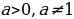
Если
Способы решения показательных уравнений.
1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.
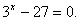
Вынесение общего множителя за скобки.
Примечание: выносим за скобки множитель с меньшим показателем.
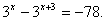
Введение новой переменной
Как правило, уравнения, решаемые этим способом, сводятся к квадратным.
Пример:
Пусть 4 x = а тогда уравнение можно записать в виде:
Сделаем обратную замену:
4 x = 4 или 4 x = 1;
х = 1 или х = 0
Ответ: х = 1 или х = 0
Определение Показательные уравнения вида 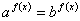
Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на 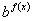
Разделим обе части уравнения на
Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.
Решение простейших показательных неравенств.
Простейшими считаются показательные неравенства вида: a x y , a x a y . (a x ≤a y , a x ≥a y ).
Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=а х является возрастающей (а1); eсли же показательная функция у=а х убывает (0), то знак нового неравенства меняют на противоположный:
a x a y → x y, если a1; знак сохранен, так как функция возрастает;
a x a y → x y, если 0; функция убывает – знак поменялся;
a x a y → x y, если a1; знак сохранен, так как функция возрастает
a x a y → x y, если 0; функция убывает – знак поменялся.
Представим правую часть в виде: 0,25=( 25 /100)=( 1 /4)=4 -1 ;
4 5-2x -1 ; функция у=4 х с основанием 41 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:
Представим число 0,16 в виде степени числа 0,4. Получаем:
0,4 2х+1 ≥0,4 2 ; основание степеней – число 0,4 — удовлетворяет условию: 0; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:
2 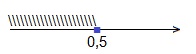
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7)
Решите систему уравнений
5)
8)
9)
1)
2)
6)
3)
4)
7) 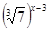
Решите систему уравнений
5)
8)
9)
Сделайте вывод по проделанной работе
От чего зависит возрастание или убывание показательной функции?
Дайте определение показательного неравенства.
Какие условия должны выполняться при решении показательных неравенств?
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Решение задач по теме «Показательные функции, уравнения и неравенства»
Разделы: Математика
1. Организационный момент.
Приветствие, проверка готовности класса к уроку.
Инструктаж по работе с Картой урока и её заполнению.
2. Мотивация и целеполагание.
В центре доски записаны слова М.В. Ломоносова:
“Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны знания, для практики сверх того, и умения”.
На откидных частях доски записаны слова “Знаю”, “Умею”.
— Несколько уроков мы были погружены в мир показательных функций, уравнений, неравенств. Посмотрите записи на доске и попытайтесь сформулировать тему урока, цель. (Слайд 1)
Учащиеся записывают тему в рабочую тетрадь.
3. Актуализация знаний.
— Посмотрите на слайд 2:
Нобелевские лауреаты в области физики
- Пьер Кюри – 1903 г
- Оуэн Ричардсон – 1928 г
- Игорь Тамм – 1958 г
- Альварес Луис – 1968 г
- Альфвен Ханнес – 1970 г
- Вильсон Роберт Вудро – 1978 г
— Что же позволило объединить в один список данных физиков?
(Учитель выслушивает ответы учащихся)
— Все они получили премию А. Нобеля за исследования в области физики с применением показательной функции.
— А что вы знаете о показательной функции?
Заполняется часть доски под словом “Знаю”.
Фронтальный опрос:
1. Какая функция называется показательной?
2. Область определения показательной функции?
3. Область значения функция?
4. Монотонность функции
5. Как называется график функции?
6. Основные методы решения показательных уравнений?
7. Методы решения показательных неравенств?
Заполняется часть доски под словом “Умею”
— Определить истинность ваших утверждений поможет работа на уроке.
Начинаем работу с математического диктанта. Будьте внимательны и собраны. Ответы записывайте в Карту урока.
Математический диктант. (Слайд 3-7 )
1. Какие из функций являются убывающими?
3) у =
5) у =
2. Какой из графиков является графиком функции 
3. Решите уравнения: 3 х+3 = 1, 4 х = 8, 5 х = 7 х
5. Решите неравенства: 2 х > 1, 0,2 х+1 4
Выполнение взаимопроверки (Слайд 8) и заполнение Карты урока.
4. Мини-ЕГЭ (проверочная работа).Слайд 9.
— Что вас ждёт в ближайшем будущем? ЕГЭ. Наша задача как можно лучше подготовиться к нему.
— В содержание экзамена, согласно кодификатору входят показательные выражения, уравнения, неравенства.
— Вам будут предложены задачи из заданий №6, №10 ЕГЭ-2015.
Проверочная самостоятельная работа “Мини-ЕГЭ” (три варианта)
Три человека работают у доски, выполняя задания, остальные в тетрадях.
Содержание проверочной работы:
В-1
1. Найдите корень уравнения: 2 4-2х = 64
2. Найдите значение выражения : 7 4/9 * 49 5/18
3. Найдите значение выражения : 18х 7 * х 13 : (3х 10 ) 2
В-2
1.Найдите корень уравнения: 5 х-7 =
2.Найдите значение выражения: 5 0,36 * 25 0,32
3.Найдите значение выражения: (7х 3 ) 2 : (7х 6 )
В-3
1. Найдите корень уравнения: ( 
2. Найдите значение выражения
3. Найдите значение выражения: (4а) 3 :а 7 * а 4
Время выполнения — 5 минут. Проверка по ключу, который находится на столе учителя. Заполнение Карты урока.
Ключ:
| Номер варианта | №1 | №2 | №3 |
| В-1 | -1 | 7 | 2 |
| В-2 | 4 | 5 | 7 |
| В-3 | 10 | 9 | 64 |
4. Практическая работа. Решение систем уравнений и неравенств.
- Работаем группами по три человека.
- Работа по учебнику: №40.29(а,б),
- Решить систему неравенств (ЕГЭ)
5. Выходной контроль.
— Решаем тест в тетрадях. В Карту записываем полученное слово.
Тест в двух вариантах
1 вариант.
Укажите промежуток, которому принадлежит корень уравнения 25 3-х =1/5.
2. Найдите корень уравнения 3 х-1 = 243.
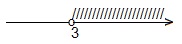
3. Укажите промежуток, являющийся решением неравенства 3 х 4 .
П) (- 
М) (4; +
4. Решите уравнение: 
И) среди ответов нет правильного.
5. 3 х + 2 – 3 х + 1 + 3 х = 21.
2 вариант.
1. Укажите промежуток, которому принадлежит корень уравнения: (1/3) х-1 =9.
А) (3;+
2. Найдите корень уравнения: 4 х-1 =256.
3. Укажите промежуток, являющийся решением неравенства
Р) (5; + 
Л) (- 
К) (10; + 
4. Решите уравнение: 
И) среди ответов нет правильного.
5. 3 х + 2 – 3 х + 1 + 3 х = 21.
— Какие слова у вас получились? Знакомы ли вам эти математики?
— Какой след они оставили в истории математики вы можете узнать самостоятельно или ждите следующих уроков.
7. Подведение итогов.
- Заполните Карту урока.
- Выставите себе оценку за работу на уроке.
8. Домашнее задание.
— Запишите в дневник д/задание: Сообщение, презентация по теме “Значение показательной функции в природе, науке, технике”, №40.49(б), №40.29(г)
9. Рефлексия.
— Проанализируйте свою работу на уроке. Заполните таблицу и сдайте Карту урока.
| Вопрос | Варианты ответа |
| Своей работой на уроке я | |
| Материал урока мне был | |
| Совпала ли оценка за урок с твоими ожиданиями? |
— Всем спасибо. Наш урок я хочу начать притчей: “Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: “Я принимаю радость в мою жизнь, но радости в моей жизни нет”. Мудрец положил перед собой ложку, свечу и кружку и попросил: “Назови, что ты выбираешь из них”. “Ложку”, – ответил юноша. “Произнеси это 5 раз”. “Я выбираю ложку”, послушно произнес юноша 5 раз. “Вот видишь”, – сказал мудрец, “повторяй хоть миллион раз в день, она не станет твоей. Надо протянуть руку и взять ложку.
— Чтобы сдать успешно ЕГЭ, надо не только мечтать и желать, но и действовать – активно заниматься на уроках и дополнительно решать задачи.
Рабочая карта урока
| Учебный элемент | Этапы урока | Примечание | Оценка |
| У1 | Математический диктант |
| № 1 | № 2 | № 3 | № 4 | № 5 | № 6 | № 7 |
Задания выполняем устно и в таблицу записываем ответы
Заполняем лист контроля.
Время – 3 минуты
Правильно
- 7 номеров-“5”
- 5-6 номеров– “4”
- 3-4 номера – “3”
- менее 3 номеров– “2”
Задания выполняем на доске,
проверяем по ключу ответы.
Заполняем лист контроля.
- 3 задания – “5”
- 2 задания – “4”
- 1 задание – “3”
Время – 4 минуты
Необходимо решить систему уравнений и задание №17 из ЕГЭ в тетради.
Если что-то забыл, посмотри в учебнике, спроси у другого.
Видео:§14 Системы показательных уравнений и неравенствСкачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:Показательные уравнения. 11 класс.Скачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📺 Видео
Решение показательных уравнений 1Скачать

Показательные уравнения. Практическая часть. 11 класс.Скачать

11 класс, 13 урок, Показательные неравенстваСкачать

Это просто! Как решать Показательные Неравенства?Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Показательные неравенства. Практическая часть. 11 класс.Скачать

Показательные неравенства и их системы. Вебинар | МатематикаСкачать

Графический метод решения показательных уравнений и неравенств Алгебра 10 (база)Скачать

Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Решение показательных уравнений и неравенствСкачать

11 класс, 12 урок, Показательные уравненияСкачать

Решение показательных уравнений | Математика ЕГЭСкачать

Показательные неравенства. Практическая часть. 11 класс.Скачать

Показательные уравнения и неравенстваСкачать

Решение показательных уравнений и неравенствСкачать

Показательные неравенства. 11 класс.Скачать


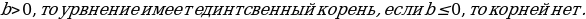
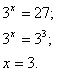

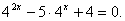
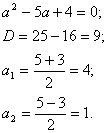
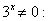
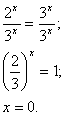
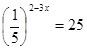
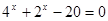
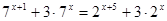
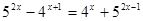
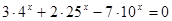
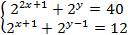
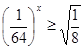
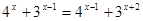
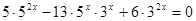
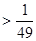

















































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);










