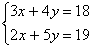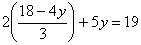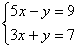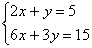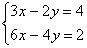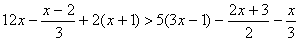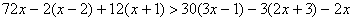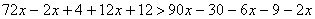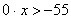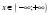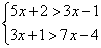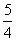Практическая работа решение линейных уравнений и неравенств

Математика. Отработка навыков решения уравнений и неравенств. Задания для самостоятельной работы.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

По теме: методические разработки, презентации и конспекты

Разработка урока по теме «Решение уравнений и неравенств с модулем»

Целью урока является совершенствование навыков решения уравнений и неравенств с модулем. В ходе урока рассматриваются рациональные приёмы и методы решения. Урок предназначен для классов с .

Решение уравнений и неравенств с параметрами

Методика решений уравнений и неравенств с параметрами. Можно использовать на факультативных занятиях и при подготовки к ЕГЭ (часть С).

Элективный курс по алгебре 11 класс «Решение уравнений и неравенств»

Рабочая программа элективного курса по алгебре 11 класс.

Программа элективного курса «Решение уравнений и неравенств с модулем.»

Элективный курс для 10 классов.

Урок по теме «Решение уравнений и неравенств с параметром»

9-й класс. Урок по теме «Решение уравнений и неравенств с параметром»Чехолкова Алла ВладимировнаЦель: Выработка навыка решения уравнений и неравенств с параметром различными способами. Разв.

Применение свойств функций к решению уравнений и неравенств

Работа посвящена одному из нестандартных методов решения уравнений и неравенств основанному на свойстве ограниченности функций, входящих в уравнение (неравенство). Предлагаемые мной задачи можно рассм.

Контрольная работа по алгебре 9 класс «Решение уравнений и неравенств второй степени с одной переменной».

Цель урока: проверить знания, умения и навыки учащихся по теме «Решение уравнений и неравенств второй степени с одной переменной».

Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

«Решение линейных уравнений, систем уравнений и неравенств»

Разработка содержит практическую работу по теме «Решение линейных уравнений,систем уравнений и неравенств» для обучающихся СПО и НПО.Проводится при повторении основного материала.

Содержимое разработки

Практическая работа по теме: «Решение линейных уравнений, систем уравнений и неравенств»

Повторить знания обучающихся в теме: « Решение линейных уравнений, систем уравнений и неравенств».

Закрепить умения и навыки решения линейных уравнений, систем уравнений и неравенств .

Определить уровень усвоения знаний, оценить результат деятельности обучающихся.

Оборудование: рабочие тетради и тетради для практических работ, ручка, калькулятор.

Продолжительность: 1 час

Ознакомиться с теоретическим материалом и решением примеров .

Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры).

В тетрадях для практических работ выполнить практическую работу .

Линейные уравнения.
Уравнение вида ax+ b=0, где a и b — некоторые постоянные, называется линейным уравнением.
Если a  0, то линейное уравнение имеет единственный корень: x = .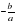
Если a=0; b  0, то линейное уравнение решений не имеет.
Если a=0; b = 0, то, переписав исходное уравнение в виде ax = -b, легко видеть, что любое x является решением линейного уравнения.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Примеры решения уравнений

2x – 3 + 4(x – 1) = 5

Пос Последовательно раскроем скобки, приведём

подобные члены и найдём x:

2x – 3 + 4x – 4 = 5

2x + 4x = 5 + 4 + 3,
6x = 12

Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:
16х-15х=88-40-12

2x – 3 + 2(x – 1) = 4(x – 1) – 7

2x + 2x – 4x = 3 +2 – 4 – 7

2x + 3 – 6(x – 1) = 4(x – 1)+ 5

2x – 6x + 3 + 6 = 4 – 4x + 5
– 4x + 9 = 9 – 4x
-4x + 4x = 9 – 9
0x = 0 Ответ: Любое число.

Системы уравнений с двумя переменными
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет.
При решении линейных систем используют метод подстановки и метод сложения.

Примеры решения систем уравнений

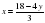
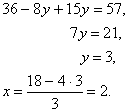
Для решения этой системы применим метод подстановки . Выразим из первого уравнения х и подставим это значение во второе уравнение системы, получим :

Ответ: (2; 3).

Для решения этой системы применим метод сложения уравнений . 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1.
Ответ: (2; 1).

Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений.
Ответ: (х; 5-2х), х–любое.

Умножим первое уравнение на –2 и сложим

С со вторым уравнением, получим 0×х+0×у=-6. Этому у уравнению не удовлетворяет ни одна пара чисел. Сл Следовательно, эта система не имеет решений.
Ответ: система не имеет решений.

Линейные неравенства с одной переменной .

Линейным называется неравенство вида ax+b0 (соответственно ax+b 0, ax+b 0), где а и b – действительные числа, причем а0.
Неравенства решаются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.

Примеры решения неравенств

2(х-3)+5(1-х) 3(2х-5)

Раскрыв скобки, получим 2х-6+5-5х6х-15
-3х-1 6х-15

-9х -14

Ответ: .

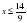
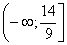
Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства:

Далее последовательно получаем:

Последнее неравенство верно при любом значении х, так как при любом значении переменной получается истинное

высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая.
Ответ:

Система неравенств
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.

Пример решения систем неравенств

x

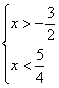
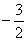
С помощью числовой прямой находим, что пересечением этих множеств служит интервал 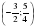. Ответ:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Решение линейных уравнений и неравенств

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практическая работа №_______

Тема: «Решение линейных уравнений и неравенств».

Цель: формирование навыков решения линейных уравнений и неравенств.

Основные теоретические сведенья.

Определение. Линейным уравнением называется уравнение вида ах= b , где а, b -числа, х- переменная.

Равносильные преобразования уравнений.

Если из одной части уравнения перенести в другую слагаемое с противоположным знаком, то получится равносильное уравнение.

Если обе части уравнения умножить или разделить на одно и то же действительное число отличное от нуля, то получится равносильное уравнение.

Определение. Линейным неравенством называется неравенство вида ах> b , ax b , где a , b -числа, х — переменная.

Равносильные преобразования неравенств.

Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное неравенство.

Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное неравенство.

Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное неравенство.

Примеры решения уравнений и неравенств.

4х 2 +20х+х+5-4х 2 +6х-2х+3=58 12-3х+4>6

х=2 x Примеры для самостоятельного решения.

а) 50х=-5 б) 8-0,8х=0 в) 2=2(3х-5)-(7-4х) г) д) е) ж) (4х+1)(3х-1)+(2х-5) 2 =(8х+1)(2х-1)

2. Решить неравенство.

а) 50х>-5 б) 8-0,8х 2(3х-5)-(7-4х) г) д) е) ж) (4х+1)(3х-1)+(2х-5) 2 (8х+1)(2х-1)

3.При каком значении t значение выражения 0,25 t -31 на 5 больше значения выражения t -18?

1. Решить уравнение.

а) 30х=-3 б) 7-0,7х=0 в) 11-(3х+1)=2х г) д) =3-х

е) ж) (2-3х) 2 +(1+4х) 2 =(5х-1)(5х+1) з) 2(х 2 -3х-1)-(2х 2 +3х-5)=1,5

а) 30х>-3 б) 7-0,7х 2 +(1+4х) 2 (5х-1)(5х+1) з) 2(х 2 -3х-1)-(2х 2 +3х-5) t значение выражения 0,25 t -31 на 0,5 больше значения выражения t -18?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 929 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Решение линейных неравенств. Практическая часть. 6 класс.Скачать

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 587 345 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 31.03.2017
• 446
• 1

• 31.03.2017
• 3125
• 1

• 31.03.2017
• 2245
• 1

• 31.03.2017
• 2465
• 10

• 31.03.2017
• 541
• 1

• 31.03.2017
• 676
• 32

• 31.03.2017
• 397
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 31.03.2017 765
• DOCX 34.8 кбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Волохо Наталья Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 20641
• Всего материалов: 16

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Швеции запретят использовать мобильные телефоны на уроках

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только на 23 февраля!
Получите новую
специальность
по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

🎥 Видео

8 класс, 40 урок, Решение линейных неравенствСкачать

Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Урок по теме РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Решение квадратных неравенств | МатематикаСкачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

A.1.3 Линейные уравнения, неравенства и системы неравенствСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Решение неравенства методом интерваловСкачать

Неравенства с двумя переменными. 9 класс.Скачать

Решение системы неравенствСкачать

Линейное неравенство с одной переменной. 6 класс.Скачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать