Практическая работа расчет сложных электрических цепей методом узловых и контурных уравнений

Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Порядок расчёта:

1. Произвольно задаёмся направлением токов в ветвях.

Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.

Красным выделены изменения после первого действия

Синим выделены изменения после третьего пункта

2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:

1. Обозначаем узлы буквами.
2. Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
   0=I1-I4-I6 (Полученное уравнение)
3. Повторяем пункт B ещё для двух узлов.
   0=-I3+I4+I5(Узел В)
   0=I3-I1-I2(Узел D)

3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы. Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.

3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)

3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)

3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.

Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3

Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5

Контур ABCA 0=I6*R6-I4*R4+I5*R5

4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.

Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.

Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.

I3=I1+I2(Узел D)

I5=I3-I4(Узел В)

I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:

Заменим токи I3 I5 I6 и получим уравнения с тремя токами :

Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:

40 = 71*I1 + 24*I2 + 14*I4

20 = 55*I1 + 93*I2 — 61*I4

0 = 60*I1 + 16*I2 — 81*I4

Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.

Правильность решения можно проверить с помощью баланса мощностей.

Видео:Метод узловых и контурных уравненийСкачать

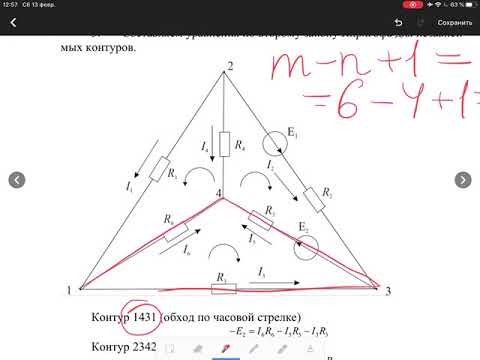
Практическая работа «Расчет электрических цепей методом узловых и контурных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Практическое занятие №15

Тема: Расчет электрических цепей методом узловых и контурных уравнений

Цель работы : научиться рассчитывать сложные электрические схемы постоянного тока методом узловых и контурных уравнений (МУКУр)

— Записать название работы, тему и цель работы

— рассмотреть и записать в конспект приведенный пример

— решить индивидуальное задание

Методика расчета сложной цепи методом узловых и контурных уравнений

Данный метод является одним из самых простейших методов расчёта электрических цепей постоянного тока любой сложности. Основывается на составлении уравнений по I и II законам Кирхгофа.

1. Определяем число ветвей m, узлов и контуров в электрической цепи. Число токов в цепи равно числу ветвей. Для каждой ветви выбираем условное направление тока и укажем их на схеме.

2. По первому закону Кирхгофа составляем уравнение для узлов в количестве n -1, где n – число узлов.

3. На основании II закона Кирхгофа составляем m – n + 1 уравнений, где m-число ветвей, n-число узлов. Для обхода выбираем контуры с меньшим числом ветвей и содержащих хотя бы одну новую ветвь. Контур обходим по часовой стрелке.

4. Полученные уравнения объединяем в систему и решаем любым способом, известным из математики.

Определить токи во всех ветвях цепи (рисунок 3), если Э.Д.С. источников энергии Е ₁ = 150В, Е ₂ = 80В, их внутренние сопротивления R ₀₁ = 1 Ом, R ₀₂ =0.5 Ом; сопротивления резисторов R ₁ =9 Ом, R ₂ =19,5 Ом, R ₃ = 25 Ом. Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощностей.

Рисунок 3 — Электрическая схема

1. На схеме произвольно показываем направления токов ветвей.

2. В задаче три неизвестных тока, для их нахождения необходимо составить систему из трех уравнений.

Первое уравнение составим для узловой точки С по первому закону Кирхгофа:

второе уравнение составим для контура АСDВА по второму закон Кирхгофа; направление обхода контура примем «по часовой стрелке»

третье уравнение составим для контура СК ND С но второму закону Кирхгофа; направление обхода контура примем «по часовой стрелке»:

3. Подставляем исходные данные в полученную систему из трех уравнений и находим значения токов ветвей:

Из второго уравнения получаем:

70=10 I ₁ – 20 I ₂ ;

Из третьего уравнения получаем:

80=20I ₂ +25 I ₃ ;

Подставляем выражения I ₁ и I ₃ в первое уравнение и находим ток I ₂ :

Определяем токи I ₁ и I ₃ :

Проверка по первому закону Кирхгофа: I ₁ + I ₂ — I ₃ =0; 5-1-4 = 0.

Ток I ₂ получился отрицательным, это значит, что первоначально произвольно принятое направление тока I ₂ от точки Dк точке С оказалось неверным и должно быть изменено на противоположное. При этом ток I ₂ будет направлен против направления Э.Д .С. Е ₂ , следовательно, источник с Э.Д.С. Е ₂ находится в режиме потребителя (например, заряд батареи аккумуляторов)

Индивидуальные задания для практической работы №15

Задача На рисунке 4 изображена схема сложной электрической цепи: Е ₁ , Е ₂ – Э.Д.С. источников энергии; R ₀₁ , R ₀₂ – их внутренние сопротивления; R ₁ , R ₂ , R ₃ – сопротивления резисторов.

Числовые значения этих параметров указаны в таблице 1

Начертить схему цепи; показать направление токов в ветвях. Определить токи ветвей I ₁ , I ₂ , I ₃ методом узловых и контурных уравнений.

Составить уравнение баланса мощностей

Перед решением задачи изучите методические указания к решению задачи и решение типового примера.

В задаче обязательно вычертить электрическую схему, соответствующую условию задачи, и показать на ней заданные и искомые величины, а также направление токов. Привести данные своего варианта.

Решение задачи сопровождается краткими пояснениями.

Текст, формулы, числовые выкладки должны быть четкими без помарок. Цифровая подстановка в уравнении должна даваться один раз без промежуточных сокращений и расчетов. Численное значение каждого символа должно обязательно занимать то же место в формуле, что и сам символ. Все расчеты необходимо вести в системе СИ. Буквенные обозначения единиц измерения ставятся только возле окончательного результата и в скобки не заключаются, например, 120 В, 13 А, 100 Вт.

Видео:Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Задачи по ТОЭ с решением и примерами

Содержание:

Метод преобразования схем

Метод преобразования электрических схем применяют для расчета сложных испей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.

Контур, состоящий из трех сопротивлений , имеющий три узловые точки , образует треугольник сопротивлений (рис. 4.6а).

Электрическая цепь, состоящая из трех сопротивлений соединенных в одной узловой точке О, образует звезду сопротивлений (рис. 4.66).

Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треуголь-• ником или наоборот.

Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками токи звезды и треугольника оставались без изменений.

Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.

Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинами и к этим обозначенным вершинам подсоединить эквивалентную звезду (или треугольник).

При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.

При замене звезды эквивалентным треугольником каждое сопротивление треугольника определяется следующими выражениями:

Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.

Пример задачи с решением 4.4

с Определить токи во всех ветвях цепи (рис. 4.7а) при следующих Исходных данных:

Решение

Дчя расчета этой цепи заменим треугольник сопротивлений, Подключенных к точкам , эквивалентной звездой, подключенной к тем же точкам (рис. 4.76).

Определим величины сопротивлений эквивалентной звезды:

Пример задачи с решением 4.6

Определить токи во всех ветвях цепи, схема которой приведена на рис. 4.8а, если задано:

Решение

Количество ветвей и соответственно различных токов в цепи (рис. 4.8а) равно пяти. Произвольно выбирается направление этих токов.

Расчетных схем две, так как в цепи два источника с ЭДС и . Вычисляются частичные токи, созданные в ветвях первым источником . этого изображается та же цепь, только вместо — его внутреннее сопротивление . Направление частичных токов в ветвях указаны в схеме рис. 4.86.

Вычисление сопротивлений и токов производится методом свертывания.

Первые частичные токи в цепи (рис. 4.86), созданные источником , имеют следующие значения:

Вычисляются частичные токи, созданные вторым источником. Для этого изображается исходная цепь, в которой источник :ЭДС заменен его внутренним сопротивлением . Направления частичных токов в ветвях указаны на схеме рис. 4.8в. 1 Сопротивления и токи определяются методом свертывания.

Вторые частичные токи в цепи (рис. 4.8в) имеют следующие значения:

Искомые токи в рассматриваемой цепи (рис. 4.8а) определяют алгебраической суммой частичных токов (см. рис. 4.8):

Ток имеет знак «минус», следовательно, его направлен и противоположно произвольно выбранному, он направлен из точ ки А в точку В.

Метод узлового напряжения

Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение между узлами и называется узловым. -узловое напряжение цепи (рис. 4.9)

Для различных ветвей (рис. 4.9) узловое напряжение можно определить следующим образом.

1. Поскольку для первой ветви ис точник работает в режиме генератор;

Величина тока определяется как

где проводимость 1-й ветви.

2. Для второй ветви источник работает в режиме потребителя следовательно

3. Для третьей ветви

(Потенциал точки для третьей ветви больше, чем потенции, точки А, так как ток направлен из точки с большим потенциалов в точку с меньшим потенциалом.)

Величину тока можно определить по закону Ома

По первому закону Кирхгофа для узловой точки А (или В):

Подставив в уравнение (4.6) значения токов из уравнений (4.3), (4.4) и (4.5) для рассматриваемой цепи, можно записать

Решив это уравнение относительно узлового напряжения , ожно определить его значение

Следовательно, величина узлового напряжения определяется от-ошением алгебраической суммы произведений ЭДС и проводимости етвей с источниками к сумме проводимостей всех ветвей.

Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т. е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус».

Таким образом, для определения токов в сложной цепи с двумя злами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5).

Узловое напряжение может получиться положительным или ггринательным, как и ток в любой ветви.

Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно ‘словно выбранному.

Пример задачи с решением 4.7

В ветвях схемы (рис. 4.10) требуется определить токи, если:

Решение

I. Узловое напряжение

где

тогда

Токи в ветвях будут соответственно равны

Как видно из полученных результатов, направление токов противоположно выбранному. Следовательно, источник работает в режиме потребителя.

Пример задачи с решением 4.8

Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: , питают потребитель (нагрузку) с сопротивлением

Как изменится ток второго генератора:

1) при увеличении его ЭДС на 1 %;

2) при увеличении узлового напряжения на 1 %.

Решение

Определяется узловое напряжение цепи (рис. 4.11)

Тогда ток второго генератора

I. При увеличении на 1 %, его величина станет равной

тогда

При этом |;довательно, увеличение ЭДС генератора на 1 % приводит личению тока этого генератора на 24 %.

2. При увеличении узлового напряжения на 1 % его величина станет равной

При этом

мм образом, ток второго генератора при увеличении узлово-.пряжения на 1 % уменьшится на 23,4 %.

Знак «минус» означает уменьшение, а не увеличение тока

Параллельное соединение генераторов

Как видно из решения примера 4.8, незначительное изменение ЭДС одного из параллельно работающих генераторов значительно изменяет ток этого генератора.

Причиной значительного изменения тока генератора может также незначительное изменение узлового напряжения 4.11), что связано с изменением сопротивлений участков или ЭДС источников.

Параллельное соединение генераторов нашло широкое примере в электрических сетях энергоснабжения потребителей осветительная и силовая нагрузка).

Значительные изменения токов генераторов, вызванные незна-пьными изменениями параметров схемы электропитания постелей от параллельно включенных генераторов, необходимо ывать при проектировании и эксплуатации электроустано-в частности тот факт, что в различное время суток работает ое количество параллельно включенных генераторов.

Увеличение ЭДС какого-либо из параллельно работающих генераторов приведет к тому, что ток этого генератора окажется в олько раз больше тока остальных генераторов. Этим обстоятельством пользуются, когда хотят «перевести нагрузку» с одного генератора на другой.

Генераторы окажутся также неодинаково загруженными при равых ЭДС, но при различных внутренних сопротивлениях. Более загруженными окажутся генераторы с меньшим внутренним сопротивлением.

И снижении ЭДС какого-либо из параллельно включенных раторов до величины узлового напряжения цепи ток в цепи этого генератора падает до нуля: . Генератор, находящийся в таком режиме, называется уравновешенным (скомпенсированным). Если ЭДС генератора станет меньше углового напряжения, то такой генератор начнет работать в режим потребителя.

Метод узловых и контурных уравнений

Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравнений по законам Кирхгофа. При составлении системы уравнения должно учитываться следующее.

1. Число уравнений равно числу токов в цепи (число токов paвно числу ветвей в рассчитываемой цепи). Направление токов на ветвях выбирается произвольно.

2. По первому закону Кирхгофа составляется уравнение где n —число узловых точек в схеме.

3. Остальные уравнения составляются по второму закону Кирхгофа.

В результате решения системы уравнений определяются иске мые величины для сложной электрической цепи (например, вс токи при заданных значениях ЭДС источников и сопротивл

Пример задачи с решением 4.9

Составить необходимое и достаточное количество уравнени* по законам Кирхгофа для определения всех токов в цепи (рис. 4.12) методом узловых и контурный уравнений.

Решение

В рассматриваемой сложной цепи имеется 5 ветвей, сдедовательно, 5 различных токов, поэтому для расчета необходимо соста вить 5 уравнений, причем 2 уравнения — по первому закон: Кирхгофа (в цепи узловых точки ) и 3 уравнения по второму закону Кирхгофа (внутренним сопротивлением ис точников пренебрегаем, т. е. = О).

Обход по часовой стрелке.

Пример задачи с решением 4.10

Определить токи в примере 4.7 методом узловых и контурных уравнений (схема рис. 4.10) при тех же заданных условиях.

Решение

При выбранном в схеме рис. 4.10 направлении токов составим необходимое и достаточное количество уравнений по законам Кирхгофа:

1.

2. (обход по часовой стрелке)

3. (обход против часовой стрелки)

К уравнение (2) подставляются значения тока из уравнения и числовые значения заданных величин. Тогда уравнения (2) будут выглядеть так:

Иля сокращения тока при суммировании уравнений (2) и (3) К числовые значения уравнения (3) умножаются на 2 (два).

Откуда

Из уравнения

И из уравнения (1):

Очевидно, что полученный результат совпадает с результатом полученным методом узлового напряжения.

Метод контурных токов

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.

Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений.

Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.

Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи . Контурный ток — это расчетная величина, измерить которую невозможно.

Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.

Для определения контурных токов составляют m уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).

Для данной схемы (рис. 4.13) необходимо составить 4 уравнено знаком «плюс» записываются ЭДС и падения напряжению разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные против контурного тока.

схема уравнений для схемы (рис. 4.13):

Решением системы уравнений вычисляются значения контурных токов, которые и определяют действительные токи в каждой схемы (рис. 4.13).

Пример задачи с решением 4.11

Определить токи во всех участках сложной цепи (рис. 4.14), если:

Решение

бходимо составить 3 уравнения по второму закону Кирхгофа для определения контурных токов (направление рных токов выбрано произвольно указано пунктирными линиями).

Подставляются числовые значения величин

Из уравнения (2) определяется ток

Значение тока (выражение (2’)) подставляется в уравнение

То же значение тока подставляется в уравнение (3):

Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим

Откуда контурный ток

Из уравнения (3) определяется контурный ток

Из уравнения (2′) определяется ток

Вычисляются реальные токи в заданной цепи:

Проверяется правильность решения для 1-го контура (рис. 4.14).

Такую же проверку можно произвести и для других контуров (2-го и 3-го):

Проверка показала правильность решения.

Метод эквивалентного генератора

Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощности и др.) только одной ветви сложной электрической цепи.

Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление , ток которого нужно определить, и всю остальную цепь, ее называют активным двухполюсником, так как эта часть имеет две клеммы , к которой и подключается сопротивление (рис. 4.15).

Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС и определенным внутренним сопротивлением азывается эквивалентным генератором.

Ток в резисторе с сопротивлением R определяют по закону Ома

Таким образом, определение тока I сводится к вычислению ЭДС эквивалентного гора и его внутреннего сопротивления

чина ЭДС определяется любым методом расчета цепей постоянного тока относительно точек при разомкнутых клеммах, т. е. в режиме холостого хода. Практически эту ЭДС можно измерить вольтметром, подключенным к клеммам лостом ходе.

реннее сопротивление эквивалентного генератора Лж вы-тся относительно точек А и В после предварительной ,i всех источников сложной схемы эквивалентного генера-х внутренними сопротивлениями.

ггически для определения внутреннего сопротивления эк-нтного генератора измеряют амперметром ток между точ-4 и В работающего двухполюсника при коротком замыка-ак как сопротивление амперметра настолько мало, что им I пренебречь. Тогда

где — напряжение холостого хода, — ток короткого замыкания

Такой метод практического определения внутреннего сопротивления эквивалентного генератора называется методом холостого хода и короткого замыкания.

Расчет параметров эквивалентного генератора, его ЭДС и ннего сопротивления , рассматриваются в примерах 4.12

Пример задачи с решением 4.12

Определить ток в сопротивлении , подключенном к точкам А ектрической цепи (рис. 4.8а) примера 4.6 методом эквивалентного генератора.

Решение

Для определения тока в сопротивлении определим ЭДС эквивалентного генератора (рис. 4.16а) и его внутреннее сопро тивление (рис. 4.166) при холостом ходе, т. е. разомкнутой цеш (между точками ).

Знак «минус» обусловлен тем, что источники в схеме включень встречно и потенциал в точке А больше потенциала в точке В, так как (см. пример 4.6).

Следовательно,

Внутреннее сопротивление эквивалентного генератора

Искомый ток

такой же ток получен в примере 4.6 на сопротивлении

Пример задачи с решением 4.13

На схеме рис. 4.17а сопротивления плеч моста равны

Сопротивление гальванометра ЭДС источника . Методом эквивалентного генератора определить в ветви гальванометра (между точками А и В).

Решение

Для определения тока в цепи гальванометра методом эквивалентного генератора необходимо вычислить ЭДС эквивалентного генератора между точками А и В (рис. 4.176) и внутреннее сопротивление эквивалентного генератора относительно точек А и В при (отсутствии гальванометра, заменив в схеме (рис. 4.17в) источник ЭДС , его внутренним сопротивлением равным нулю.

Для определения ЭДС эквивалентного генератора принимают потенциал точки С схемы (рис. 4.176) равным нулю, т. е.

При замене источника ЭДС его внутренним сопротивле-нием, равным нулю, замыкаются накоротко точки С и D схемы (рис. 4.17в). При этом (рис. 4.17г) сопротивления соединены между собой параллельно. Также параллельно соединены между собой сопротивления . Между точками А и В сопротивления соединены последовательно. Следовательно, сопротивление эквивалентного генератора относительно точек А и В будет равно

Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с меньшим потенциалом (рис. 4.17а), будет равен

Эти страницы вам могут пригодиться:

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎬 Видео

Законы Кирхгофа. Метод контурных уравненийСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Лекция 117. Правила КирхгофаСкачать

Электротехника (ТОЭ). Лекция 10. Потенциальная диаграмма | Решение задачСкачать

Применение законов Кирхгофа при решении задачСкачать

46 Алгоритм решения метода узловых и контурных уравненийСкачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

2 7 Методы расчета цепей постоянного токаСкачать

Урок 7. ЗАКОН ОМА простыми словами с примерамиСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

ТОЭ - Метод двух узлов│Самое подробное решение задачиСкачать

Метод контурных токовСкачать

Практическая работа №2. Часть 1Скачать

1 4 3 Метод узловых напряжениеСкачать

Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать