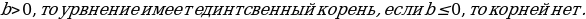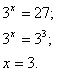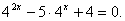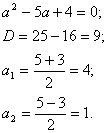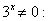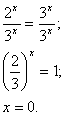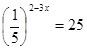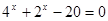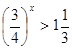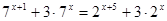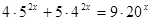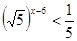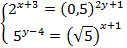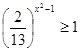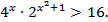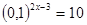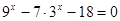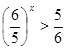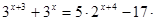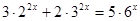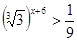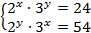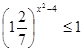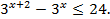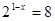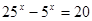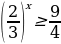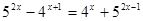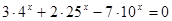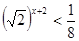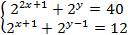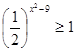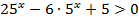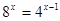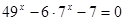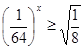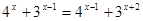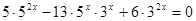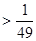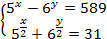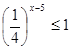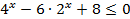Практическая работа по теме показательные уравнения ответы

Видео:Показательные уравнения. Практическая часть. 11 класс.Скачать

Практическая работа по теме: «Решение показательных уравнений и неравенств»

Просмотр содержимого документа
«Практическая работа по теме: «Решение показательных уравнений и неравенств»»

Практическая работа №3

Тема: «Решение показательных уравнений и неравенств»

Цель: научиться применять свойства показательной функции для решения показательных уравнений и неравенств, закрепить знания и умения по применению методов решения показательных уравнений и неравенств для решения практических задач.

Основные теоретические положения

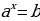
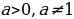
Определение. Уравнение вида , где , называется показательным.

Если

Способы решения показательных уравнений.

1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.

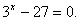
Вынесение общего множителя за скобки.

Примечание: выносим за скобки множитель с меньшим показателем.

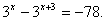
Введение новой переменной

Как правило, уравнения, решаемые этим способом, сводятся к квадратным.

Пример:

Пусть 4 x = а тогда уравнение можно записать в виде:

Сделаем обратную замену:

4 x = 4 или 4 x = 1;
х = 1 или х = 0

Ответ: х = 1 или х = 0

Определение Показательные уравнения вида 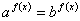называются однородными.

Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на .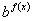

Разделим обе части уравнения на

Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.

Решение простейших показательных неравенств.

Простейшими считаются показательные неравенства вида: a x y , a x a y . (a x ≤a y , a x ≥a y ).

Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=а х является возрастающей (а1); eсли же показательная функция у=а х убывает (0), то знак нового неравенства меняют на противоположный:

a x a y → x y, если a1; знак сохранен, так как функция возрастает;

a x a y → x y, если 0; функция убывает – знак поменялся;

a x a y → x y, если a1; знак сохранен, так как функция возрастает

a x a y → x y, если 0; функция убывает – знак поменялся.

Представим правую часть в виде: 0,25=( 25 /₁₀₀)=( 1 /₄)=4 -1 ;

4 5-2x -1 ; функция у=4 х с основанием 41 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:

Представим число 0,16 в виде степени числа 0,4. Получаем:

0,4 2х+1 ≥0,4 2 ; основание степеней – число 0,4 — удовлетворяет условию: 0; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:

2 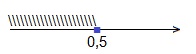х≤2-1;

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

Сделайте вывод по проделанной работе

От чего зависит возрастание или убывание показательной функции?

Дайте определение показательного неравенства.

Какие условия должны выполняться при решении показательных неравенств?

Видео:Показательные уравнения. 11 класс.Скачать

Практическая работа «Решение показательных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: «Показательные уравнения» Цель работы:

1. Формировать умения и навыки решения показательных уравнений (закрепление и систематизация знаний о методах решения показательных уравнений и выработку самостоятельно решать показательные уравнения).

2. Формировать умения и навыки самостоятельного умственного труда

3. Прививать умения и навыки работы со справочным материалом 4. Определить уровень остаточных знаний студентов по данной теме Перечень справочной литературы :

1. Башмаков, М. И. Математика: алгебра и начала анализа, геометрия: учеб. для студ. учреждений сред. проф. Образования / М.И. Башмаков. – 4-е изд., стер. – М.: Издательский центр «Академия», 2017. – 256 с. ISBN 978-54468-5988-7; 2. Башмаков, М. И. Математика: алгебра и начала анализа, геометрия: Задачник: учеб. для студ. учреждений сред. проф. образования / М.И. Башмаков. – 4-е изд., стер. – М.: Издательский центр «Академия», 2017. – 416 с. ISBN 978-5-4468-5127-0;

3. указания по выполнению практической работы; 4. рабочая тетрадь с конспектами, тетрадь справочник. Краткие теоретические сведения:

Определение: Показательным уравнением называется уравнение, в котором переменная содержится в показателе степени.

Простейшее показательное уравнение – это уравнение вида:

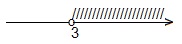
а х = b, где а >0, а ≠1, b>0. Уравнение a x = b не имеет корней, если b

Методы решения показательных уравнений:

1. Уравнивание оснований.

1. Уединить слагаемое, содержащее переменную.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Практическая работа №5
учебно-методический материал по алгебре на тему

Практическая работа №5

Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Скачать:

Видео:Алгебра 10 класс (Урок№22 - Показательные уравнения. Системы показательных уравнений.)Скачать

Предварительный просмотр:

ПРАКТИЧЕСКАЯ РАБОТА № 5

Тема: Решение показательных уравнений и неравенств.

Вид занятия: Практическое занятие.

Проверить знания и практические умения студентов решать показательные уравнения и неравенства

Обеспечить высокую творческую активность при выполнении практической работы.

Математика (школьный курс)

Физика, техническая механика, электротехника, химия, экономика, курсовое и дипломное проектирование

Использование ИКТ (информационно – коммуникационных технологий)

(мультимедийные презентации, проекционное оборудование, интерактивная доска, персональный компьютер, компьютерное тестирование)

Наглядные пособия и раздаточный материал: методические указания для практической работы №5, плакат «Свойства степеней»

Литература: Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М.: Просвещение, 2012

Определение типов показательных уравнений и методов их решения, решение простейших показательных неравенств.

Определение. Уравнение вида , где , называется показательным.

Если

Способы решения показательных уравнений.

1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.

1. Вынесение общего множителя за скобки.

Примечание: выносим за скобки множитель с меньшим показателем.

1. Введение новой переменной

Как правило, уравнения, решаемые этим способом, сводятся к квадратным.

Пусть 4 x = а тогда уравнение можно записать в виде:

Сделаем обратную замену:

4 x = 4 или 4 x = 1;
х = 1 или х = 0

Ответ: х = 1 или х = 0

Определение Показательные уравнения вида называются однородными.

Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на .

Пример: 2 x = 3 x

Разделим обе части уравнения на

Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.

Решение простейших показательных неравенств.

Простейшими считаются показательные неравенства вида: a x y , a x >a y . (a x ≤a y , a x ≥a y ).

Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют , если функция у=а х является возрастающей (а>1 ); eсли же показательная функция у=а х убывает (0 ), то знак нового неравенства меняют на противоположный :

a x a y → x y, если a>1 ; знак сохранен, так как функция возрастает;

a x > a y → x > y, если a>1 ; знак сохранен, так как функция возрастает

Представим правую часть в виде: 0,25=( 25 / 100 )=( 1 / 4 )=4 -1 ;

4 5-2x -1 ; функция у=4 х с основанием 4>1 возрастает на R , поэтому, опуская основания степеней, знак неравенства сохраним:

Представим число 0,16 в виде степени числа 0,4. Получаем:

0,4 2х+1 ≥ 0,4 2 ; основание степеней – число 0,4 — удовлетворяет условию: 0 ; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:

🎥 Видео

№18 Показательные уравнения с параметром. Подготовка к ЕГЭ по математике.Скачать

11 класс, 12 урок, Показательные уравненияСкачать

Показательные уравнения | Алгебра 11 класс #8 | ИнфоурокСкачать

Показательные уравнения — что это такое и как решатьСкачать

Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Показательные неравенства. Практическая часть. 11 класс.Скачать

Методы решения показательных уравнений. Урок №25.Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ😩 #математика #shorts #егэ #огэ #уравнение #показательныеуравненияСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

§12 Показательные уравненияСкачать

Как решать Показательные Уравнения? (часть 2)Скачать

Математика это не ИсламСкачать

Показательные неравенства. Практическая часть. 11 класс.Скачать

Показательные уравнения в ЕГЭ 🥊Скачать