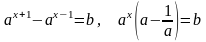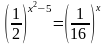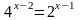Практическая работа корни уравнений равносильность уравнений преобразование уравнений (7 видео)

Практическая работа корни уравнений равносильность уравнений преобразование уравнений

Цель: формирование навыков преобразования и решения уравнений.

Вид работы: индивидуальный.

Время выполнения: 2 часа.

Теоретические сведения

Уравнения, имеющие одно и то же множество корней, называются равносильными.

Уравнения, не имеющие корней, также являются равносильными.

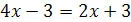
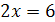
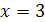
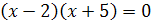
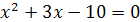
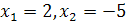
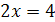
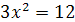
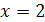
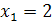
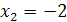
Например, уравнения и равносильны, так как каждое из них имеет только один корень . Уравнения и также равносильны, так как они имеют одни и те же корни . Уравнения и не равносильны, так как первое имеет корень , а второе – корни и .

Два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого уравнения.

Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.

При этих преобразованиях исходное уравнение заменяется на равносильное ему уравнение.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.

Из этого определения и определения равносильности уравнений следует, что:

1) если два уравнения равносильны, то каждое из них является следствием другого;

2) если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.

При решении уравнений главное – не потерять корни, а наличие посторонних корней можно установить проверкой.

Посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное.

Потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.

При решении уравнения можно делать только такие его преобразования, при которых не происходит потерь корней. Если при этом получаются уравнения – следствия данного, то необходима проверка найденных корней.

Пример 1. Решить уравнение .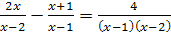

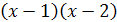
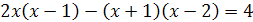
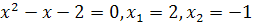
Решение. Умножив обе части уравнения на общий знаменатель всех трех дробей, т.е. на , получим , откуда .

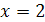
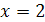
Проверка. 1) При знаменатели двух дробей уравнения равны нулю. Поэтому не является корнем данного уравнения.

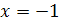
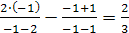
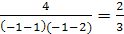
2) При левая часть уравнения равна , правая часть равна .

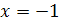
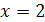
Таким образом, корнем уравнения является , а корень — корнем данного уравнения не является, его называют посторонним корнем.

Пример 2. Решите уравнение .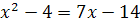

Решение. Преобразуем данное уравнение так:

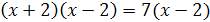
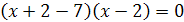
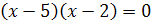
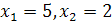
Откуда , т.е. , следовательно, .

Задания к практической работе

Задание 1. Равносильны ли следующие уравнения:

1. и ;

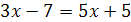
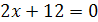
2. и ;

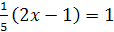
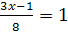
3. и ;

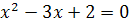
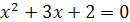
4. и ;

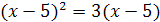
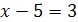
5. и ;

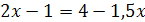
6. и ;

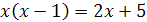
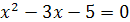
7. и ;

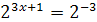
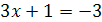
8. и .

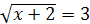
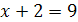
Задание 2. Решите уравнения:

1. 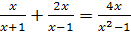;	2. ;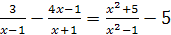
3. 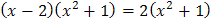;	4. .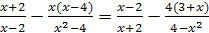

Контрольные вопросы

1. Какие уравнения называются равносильными? Приведите примеры.

2. Какое уравнение называется следствием другого? Приведите примеры.

3. Какие методы преобразования уравнений вы знаете?

Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1.

Содержание

Основные приемы решения уравнений
Просмотр содержимого документа «Основные приемы решения уравнений»
Практическое занятие .Нахождение корней уравнений. Равносильность уравнений. Преобразование уравнений.
🎬 Видео

Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Основные приемы решения уравнений

Практическое занятие по теме: Основные приемы решения уравнений

Просмотр содержимого документа
«Основные приемы решения уравнений»

Практическое занятие Приложение 29

Основные приемы решения уравнений.

Корни уравнений. Равносильность уравнений. Преобразование уравнений.

1) Теоретический этап. Опорный конспект.

Уравнением с одной переменной x называется выражение f(x) = g(x), содержащее переменную величину x и знак равенства.

Число a называется корнем уравнения f(x) = g(x), если при подстановке этого числа в уравнение получается верное числовое равенство.

Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим уравнением, ему равносильным. Такая замена называется тождественным преобразованием.

Основные тождественные преобразования:

Замена одного выражения другим, тождественно равным ему.

Например, уравнение (3x+ 2) 2 = 15x+10 можно заменить следующим равносильным:

Перенос членов уравнения из одной стороны в другую с обратными знаками.

Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком « – »: 9x 2 + 12x + 4 – 15x – 10 = 0, после чего получим: 9x 2 – 3x – 6 = 0 .

Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение (x – 1)(x – 3 ) = 0, у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление может привести к потере корня. Так, если (x – 1)(x – 3) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x – 3 .

Можно возвести обе части уравнения в нечетную степень или извлечь из обеих частей уравнения корень нечетной степени. Необходимо помнить, что: а) возведение в четную степень может привести к приобретению посторонних корней;

б) неправильное извлечение корня четной степени может привести к потере корней.

Уравнение 7x = 35 имеет единственный корень x = 5. Возведя обе части этого уравнения в квадрат, получим уравнение: 49x 2 = 1225 , имеющее два корня: x = 5 и x = – 5. Последнее значение является посторонним корнем.

Неправильное извлечение квадратного корня из обеих частей уравнения 49x 2 = 1225 даёт в результате 7x = 35,и мы теряем корень x = – 5. Правильное извлечение квадратного корня приводит к уравнению: | 7x | = 35, следовательно, к двум случаям: 1) 7x = 35,

тогда x = 5; 2) – 7x = 35, тогда x = – 5. Следовательно, при правильном извлечении квадратного корня мы не теряем корней уравнения.

1) Если показательное уравнение сводится к виду a x = a b (1) где a 0 и a ≠1, то оно имеет единственный корень х = b.

2) Иногда, чтобы привести показательное уравнение к виду (1), необходимо в левой части уравнения вынести за скобки общий множитель а х , например:

3) Некоторые показательные уравнения заменой а х = t сводятся к квадратным.

Надо помнить, что t 0, так как показательная функция не может принимать отрицательные значения.

Чаще всего при решении логарифмического уравнения его приводят к виду

Решив полученное уравнение, следует сделать проверку корней, чтобы исходное уравнение не потеряло смысл.

2) Подготовительный этап. Перепишите и заполните пропуски:

Пример 1. Решить уравнение: 9 х – 7 3 х = — 12

9 х – 7 3 х = — 12; Пусть 3 х = t , t 0; t 2 — 7t + 12=0; D = 1; t₁ = 3, t ₂= 4.

Делаем обратную замену 1) 3 x = 3; 2) 3 x = 4

x₁ = …; x ₂ =

Ответ: х₁ = 1; x ₂ = .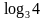

Пример 2. Решить уравнение:

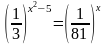
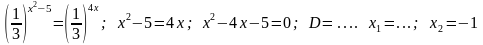
Решение: . _{Уравниваем основания :}.

Пример 3. Решить уравнение: log₅ (x 2 — 10) = log ₅ 9x

Решение: log₅ (x 2 — 10) = log ₅ 9x; x 2 — 9x – 10 = 0, D = …; x₁=10, x₂= -1

Проверка: при х = 10, log₅ (10 2 — 10) = log ₅ (9 ∙10) – верно

Пример 4. Решить уравнение: log ₇ (x 2 + 6x) = 1;

Решение: log ₇ (x 2 + 6x) = 1;

x 2 + 6x =7 1 ; x 2 + 6x – 7 = 0; D = 64; x₁ = — 7 u x₂ = …

Проверка: при х = — 7, log ₇ ((- 7) 2 + 6 ∙(-7)) = 1 – верно

при х = 1, log ₇ (1 2 + 6 ∙1) = 1 – верно

Пример 5. Решить уравнение log₂ (x – 5) + log₂ (x +2) = 3

Используем свойство логарифмов: log₂(( x-5)(x + 2)) = 3; (x-5)(x+2) = 2 3 ; (x-5)(x+2) = 8;

х 2 + …х – 5х – 10 = 8; x 2 – 3x — 18 = 0; D = …; x₁ = – 3; x₂ = ….

Проверка: при x = – 3, log₂ (– 3 – 5) + log₂ (– 3 +2) = 3 – неверно

При х = 6, log₂ (6 – 5) + log₂ (6 + 2) = 3 – верно

Пример 6. Решить уравнение: .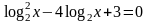

Решение:

Пусть 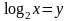, тогда у 2 – 4у + 3 = 0; D = …; у₁ = 1; у₂ = …

Сделаем обратную подстановку:

1) = 1; х = 2; 2) = 3; х = 2 3 ; х = …

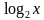
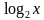
Ответ: х = 2, х = 8.

3) Практический этап.

1. Решить уравнение: 4 х – 6 ∙ 2 х = – 8

2. Решить уравнение:

3. Решить уравнение: log₃ (x 2 + 6) = log₃ 5x

4. Решить уравнение: log₁₂ (x 2 – x) = 1

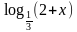
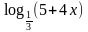
5. Решить уравнение: + = 0

6. Решить уравнение: log 2 ₂ Х – 4 log ₂ Х = 12

4) Дополнительные задания *

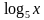
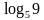
1. Укажите промежуток, которому принадлежит корень уравнения: + = 3

1) [ – 10; – 15] ; 2) (5; 10); 3) (10; 13); 4) [ 10; 15]

2. Укажите промежуток, которому принадлежит корень уравнения: 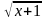х = 1

1) [ 2; 5] ; 2) (– 2; – 1); 3) [– 1; 1]; 4) [ 1; 2]

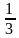
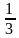
3. Найдите сумму корней уравнения: ( ) 2х + 5∙ ( ) х – 24 = 0

4.Укажите промежуток, которому принадлежит корень уравнения: log ₅ (3х – 1) = 3

1) (15; 20) ; 2) [ 0; 2]; 3) (20; 40); 4) [ 40; 50]

5. Найдите сумму корней уравнения: 3 2х – 4 3 х + 3 = 0

6. Решите уравнение lg(5х + 11) – lg( 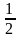) = lg13

7. Решите уравнение:

Видео:Алгебра 7 класс (Урок№47 - Равносильность уравнений и систем уравнений.)Скачать

Практическое занятие .Нахождение корней уравнений. Равносильность уравнений. Преобразование уравнений.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Практическое занятие № 19.Нахождение корней уравнений. Равносильность уравнений. Преобразование уравнений.

Цель занятия :
Владение стандартными приемами находить корни, обобщать, систематизировать, видеть равносильность преобразования уравнений.
Образец решения:
Пример 1
Уравнения х 2 -4=0 и (х+2)*(2х-4)=0 — равносильны?
Решение:
Решим первое уравнение:х 2 -4=0 имеет корни х=±2, т.к. х 2 =4;

Решим второе уравнение (х+2)*(2х-4)=0, т.к. х+2=0, x=-2 или 2х-4=0, 2х=4, х=2.

Ответ: да, так как имеют одинаковые корни.

Пример 2
Проверить на равносильность уравнения: х 2 +1=0 и =0.
Решение:
х 2 +1=0 –не имеет корней в области действительных чисел R=(-∞; +∞)

и =0.-не имеет корней в области R=-∞; +∞

Ответ: равносильны, так как они не имеют корней.
Пример 3
Определить уравнение-следствие при решении уравнений x-2=3 и х 2 -25=0. Решение:
Уравнение x-2=3 имеет корень 5, уравнение х 2 -25=0 имеет корни ± 5. Так как корень уравнения x-2=3 является корнем уравнения х 2 -25=0, то уравнение х 2 -25=0 является следствием уравнения x-2=3.
Пример 4
Решить двумя способами уравнения и сделать вывод:
а) = х-1;б) =

х≥-11 , далее возведём обе части уравнения в квадрат:

х 2 -3х-10=0, решим его через дискриминант
х ₁ =-2; х ₂ =5.Оба корня принадлежат ОДЗ уравнения, но это не меняет сути дела и мы вынуждены выполнить проверку корней.
Проверка: при х ₁ =-2, получим -2+11=-2-1 — неверное равенство, х ₁ =-2 — посторонний корень;
при х ₂ =5, получим 5+11=5-1 или 4=4 — верное равенство, 5 — корень исходного уравнения.
Ответ: 5
второй способ:
Исходное уравнение равносильно системе:

Решение системы исходного уравнения х2=5 . Ответ: 5
б ) =

Решений нет
Значит, ОДЗ уравнения пустое множество, уравнение решений не имеет
Ответ: корней нет
второй способ:
Исходное уравнение равносильно системе:

Системы решений не имеют, значит, и исходное уравнение тоже решений не имеет
Ответ: корней нет.
Вывод: При решении иррациональных уравнений – возведение обеих частей уравнения в четную степень, принадлежность полученных корней ОДЗ уравнения не позволяет сделать вывод, о том являются ли эти корни посторонними или нет. Поэтому выполнение проверки корней обязательно и это этап решения уравнения. Если корень не принадлежит ОДЗ, то он, конечно, посторонний корень уравнения. В то же время, записывая систему равносильную уравнению, мы не нарушаем логики решения: ведь уравнение с пустой ОДЗ равносильно системе, не имеющей решений.
Пример 5
Решить уравнение: │2х-3│=5

Решение: Данное уравнение равносильно системам, на основании определения модуля:│ а│

Пример 6
Являются ли уравнения равносильными: 2 х -2 х-4 =15 и х+=7?

2 х -2 х-4 =15 – показательное уравнение
По свойству степеней:
2 х -2 х :2 4 =15, 2 х (1-=15; 2 х * =15 , 2 х =16, х=4 – корень уравнения х+=7 – иррациональное уравнение
ОДЗ:
25-х 2 ≥0
х ∈( -5; 5)

Данное уравнение равносильно системе:

2х 2 -14х+24=0 ,разделим все коэффициенты на 2

х1=4, х2=3- корни уравнения
Ответ: неравносильны, так как уравнения имеют не одинаковые корни.

1 вариант
1. Уравнения х 2 -9=0 и (х+3)*(3х-18)=0 — равносильны?
2.Решить 2-мя способами уравнение:
=х+2 и сделать вывод
3.Равносильны ли уравнения:
5 х+1 +5 х =750 и х 2 -9=0?

4.Решить уравнение:
sin4х=0 и вычислить полученный результат при k=0; ±2

5.Найти корень уравнения:

1.Уравнения х 2 -64=0 и (х+8)*(4х-32)=0 — равносильны?
2.Решить 2-мя способами уравнение:
и сделать вывод
3.Равносильны ли уравнения:
6 х+2 -6 х =35 и х 2 =0?

4.Решить уравнение:
cos6х=1 и вычислить полученный результат при k=0; ±12