Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.
- Поворот точки вокруг точки
- Полный оборот
- Угол поворота
- Направление поворота
- Величина угла поворота, угол произвольной величины
- Поворот фигуры вокруг точки на угол
- Поворот точек на произвольный угол онлайн
- Синтаксис
- Примеры
- Компьютерная Графика
- Двумерный алгоритм преобразование в новые координаты
- Поворот.
- 📸 Видео
Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Поворот точки вокруг точки
Центр поворота – точка, относительно которой осуществлен поворот.
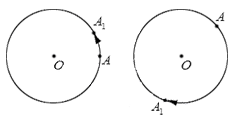
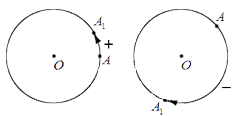
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .
Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.
Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:
Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Полный оборот
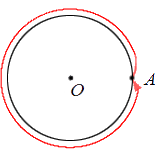
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .
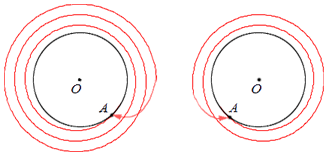
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:
В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Угол поворота
Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.
Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.
Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .
Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .
Разберем характеристики угла поворота подробнее.
Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Направление поворота
Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.
Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Величина угла поворота, угол произвольной величины
Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.
Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;
Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.
Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.
Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.
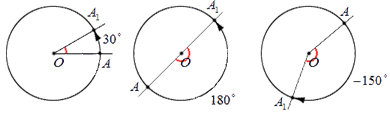
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :
Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:
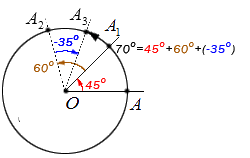
Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:
Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .
По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .
Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.
В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.
При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .
Видео:Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать

Поворот фигуры вокруг точки на угол
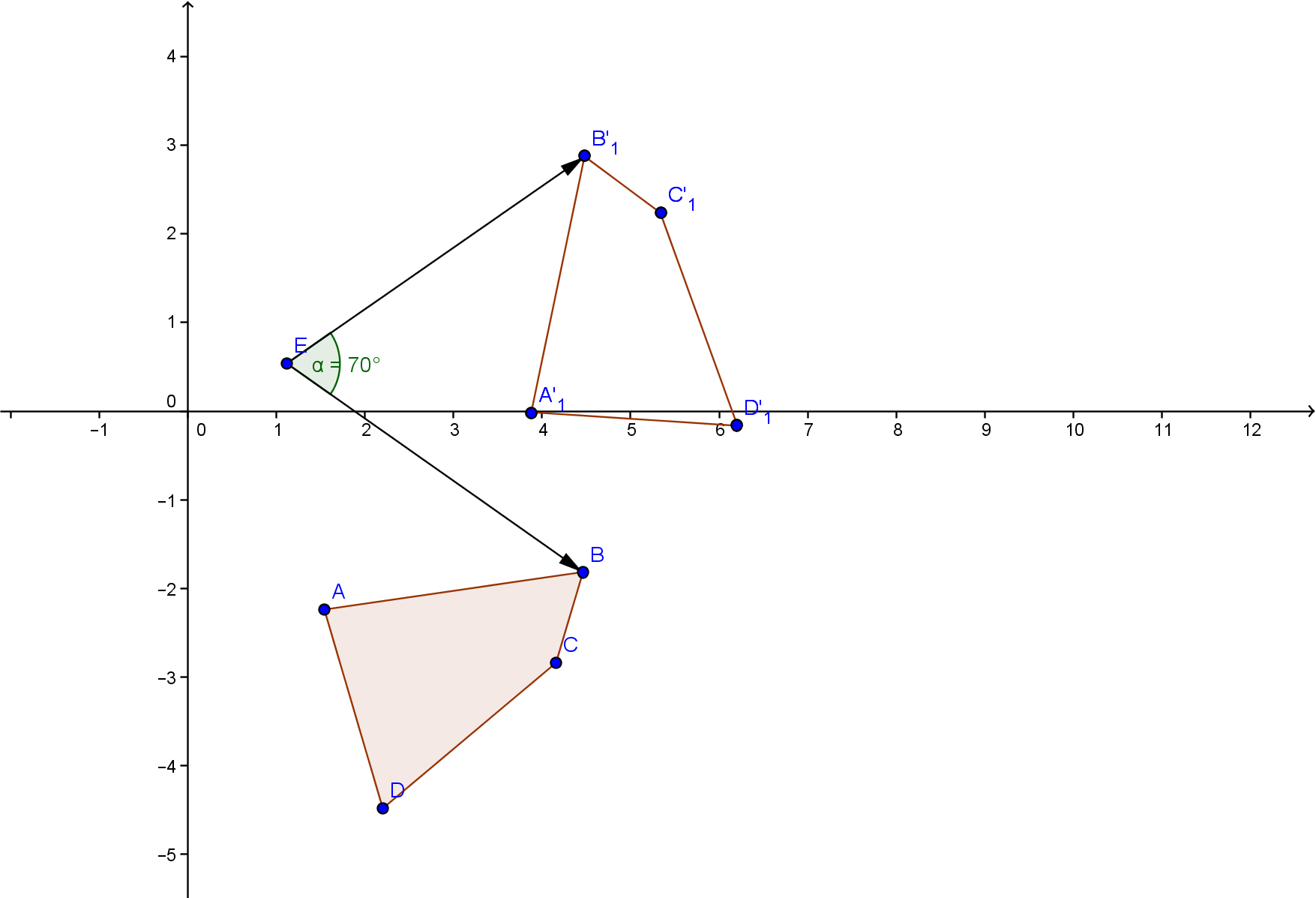
Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).
Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .
Видео:§22 Поворот точки вокруг начала координатСкачать

Поворот точек на произвольный угол онлайн
| Координаты фигуры, разделенные через пробел |
| Угол поворота в градусах (если положительное то против часовой стрелки) |
| Точка относительно которой проводится поворот |
| Новые координаты полученные при повороте фигуры(точки) на заданный угол |
Поворот — это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству. Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  СинтаксисКоординаты — строка, содержащая координаты в виде x:y (где x — абсцисса координаты, y — ордината координаты), разделенные хотя бы одним пробелом Точка вращения — точка, относительно которой будет осуществляться поворот, всех заданных координат. Поворот в градусах — поворот фигуры на заданный угол. Если число положительное — то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке. Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  ПримерыПример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7) Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3 Видео:Уравнение окружности (1)Скачать  Компьютерная ГрафикаВидео:9 класс, 33 урок, ПоворотСкачать  Двумерный алгоритм преобразование в новые координатыВидео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать  Поворот.Пусть необходимо повернуть точку P(x, y) вокруг начала координат O на угол (фи) . Изображение новой точки на рис. 2.2. обозначим через P’(x’, y’). Всегда существуют четыре числа a, b, c, d, такие, что новые координаты могут быть вычислены по значениям старых координат x и y из следующей системы уравнений: Для получения значений a, b, c, d рассмотрим вначале точку (x, y) = (1, 0). Полагая x =1 и y =0 в уравнении (2.1), получим Но в этом простом случае, как это видно из рис. 2.3(а), значения x’ и y’ равны соответственно Cos (фи) и Sin (фи). Тогда будем иметь: Аналогичным образом из рис. 2.3(б) следует Тогда вместо системы уравнений (2.1) можем записать Система уравнений (2.2) описывает поворот вокруг точки O — начала системы координат. Но часто это не то, что нам нужно. Если требуется выполнить поворот относительно заданной точки, то в этих уравнениях можно заменить: x — на (x-xo) , y — на (y-yo), x’ — на (x`-xo) и y’ — на (y`-yo) (сдвигаем систему координат) . Система уравнений, которая описывает поворот точки вокруг любой точки: Система уравнений (2.3) неудобна для реализации на PC. Применяем матричную запись. 📸 Видео§35 Формулы поворота координатных осейСкачать  Как искать точки на тригонометрической окружности.Скачать  Видеоурок "Преобразование координат"Скачать  Сферическое движениеСкачать  Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать  9 класс, 7 урок, Уравнение прямойСкачать  Формула поворота РодригаСкачать  ПоворотСкачать 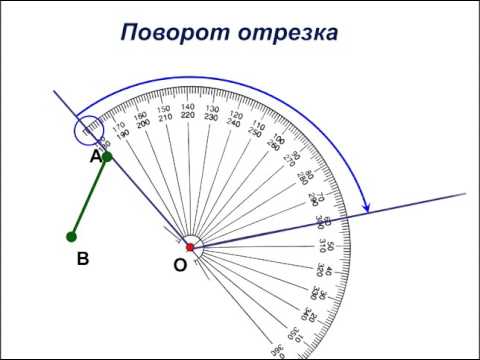 |
 (2.1)
(2.1) 


 (2.2)
(2.2)  (2.3)
(2.3)