Алгебраические уравнения поверхностей

Напомним, что многочленом степени одной переменной называется выражение вида

где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .

Многочленом трех переменных называется выражение вида

называется степенью многочлена трёх переменных.

Алгебраической поверхностью называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида

где — многочлен трех переменных .

Уравнение вида (4.11) называется алгебраическим уравнением с тремя неизвестными. Степенью уравнения (4.11) называется степень многочлена . Одна и та же поверхность может быть задана уравнением вида (4.11) с многочленами разных степеней. Порядком алгебраической поверхности называется наименьшая из степеней этих многочленов.

Всякую неалгебраическую поверхность называют трансцендентной.

В примере 4.1,а,б,в,г — поверхности алгебраические: а — первого порядка. б,в,г — второго порядка. Примером трансцендентной поверхности служит цилиндрическая поверхность (см. рисунок), образующие которой, параллельные оси , пересекают координатную плоскость в точках синусоиды . Эту линию нельзя задать уравнением вида (4.11).

Содержание

Теорема (4.1) об инвариантности порядка алгебраической поверхности
Порядок поверхности.
Кривые 3-го и 4-го порядка
СОДЕРЖАНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
🔍 Видео

Видео:Поверхности второго порядкаСкачать

Теорема (4.1) об инвариантности порядка алгебраической поверхности

Если в некоторой аффинной системе координат в пространстве поверхность задана уравнением (4.11), то и в любой другой аффинной системе координат эта поверхность задается уравнением того же вида (4.11) и той же степени. Другими словами, порядок алгебраической поверхности является инвариантом (остается неизменным в любой аффинной системе координат).

Теорема доказывается аналогично теореме 3.1.

В аналитической геометрии в пространстве изучаются:

– алгебраические поверхности первого порядка , описываемые алгебраическим уравнением первой степени с тремя неизвестными

– алгебраические поверхности второго порядка , описываемые алгебраическим уравнением второй степени с тремя неизвестными

1. Теорема 4.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных

где , степень многочлена не изменяется.

2. Алгебраическое уравнение (4.11) может не иметь действительных решений. Например, в пространстве нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теореме алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (4.11) вида , где задает некоторую алгебраическую поверхность в трехмерном комплексном пространстве (см. пункт 2 замечаний 2.9). Если все точки этой поверхности вещественные (действительные), т.е. а то поверхность называют вещественной (действительной). В противном случае поверхность называют мнимой.

3. Алгебраическими неравенствами с тремя неизвестными называются неравенства вида

где — многочлен трех переменных . Степенью алгебраического неравенства называется степень многочлена .

4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.

5. Многочлен второй степени

называется также квадратичной функцией трех переменных; многочлен

называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.

6. Квадратичную функцию (см. пункт 5) можно записать:

а) в матричном виде

где — матрица квадратичной функции; — расширенный (дополненный единицей) столбец переменных;

б) выделяя квадратичную и линейную части:

где — матрица квадратичной формы, — столбец коэффициентов линейной формы, — столбец переменных.

Матрицы и называются также матрицами малой и большой квадратичных форм квадратичной функции .

7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).

8. Теорема 4.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт 5 замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Порядок поверхности.

В пространстве аналитическая геометрия изучает поверхности, которые в прямоугольных декартовых координатах определяются алгебраическими уравнениями первой, второй и т.д. степени относительно X,Y,Z:

Ax+By+Cz+D=0 (1)

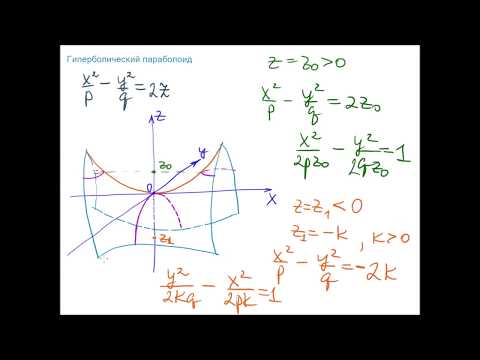
Аx²+By²+Cz²+2Dxy+2Exz+2Fyz+2Mx+2Ny+2Lz+K=0 (2)

и т.п. Порядок уравнения называется порядком поверхности им определяемой. Мы уже видели, что уравнение первого порядка (линейное) (1) всегда задаёт плоскость — это единственная поверхность первого порядка. Поверхностей второго порядка уже много. Рассмотрим наиболее важные из них.

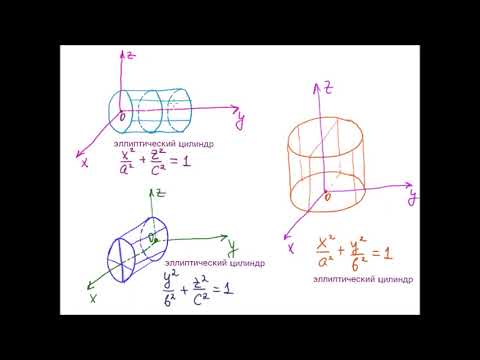
§2. Цилиндрические поверхности с образующими, параллельными одной из координатных осей.

Пусть в плоскости XОY, например, задана некоторая линия L, её уравнение есть F(x,y)=0 (1) . Тогда множество прямых, параллельных оси oz (образующие) и проходящих через точки на L, образуют поверхность S, называемую цилиндрической поверхностью.

Покажем, что уравнение (1), не содержащее переменной z, и есть уравнение этой цилиндрической поверхности S. Возьмём произвольную точку М(x,y,z), принадлежащую S. Пусть образующая, проходя через М пересекает L в точке N. Точка N имеет координаты N(x,y,0), они удовлетворяют уравнению (1), т.к. (·)N принадлежит L. Но тогда и координаты (x,y,z,) удовлетворяют (1), т.к. оно не содержит z. Значит, координаты любой точки цилиндрической поверхности S удовлетворяют уравнению (1). Значит, F(x,y)=0 — уравнение этой цилиндрической поверхности. Кривая L называется направляющей (кривой) цилиндрической поверхности. Заметим, что в пространственной системе L должна задаваться, вообще-то, двумя уравнениями F(x,y)=0 , z=0, как линия пересечения.

1) Если направляющей служит окружность x²+y²=R², то соответствующая поверхность называется круговым цилиндром.

2)
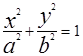
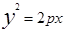
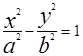
Уравнения , , задают в пространстве соответственно эллиптический цилиндр, параболический цилиндр, гиперболический цилиндр.

Направляющими в плоскости хоу являются эллипс, парабола, гипербола. Очевидно, уравнения F=(y,z)=0 и F(x,z)=0 задают соответственно цилиндрические поверхности с образующими параллельными оси OX и OY. Их направляющие лежат в плоскостях YOZ и XOZ соответственно.

Замечание. Цилиндрическая поверхность не обязательно является поверхностью второго порядка. Например, 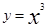есть цилиндрическая поверхность 3го порядка, а уравнение y=sin(x) задаёт синусоидальный цилиндр, которому никакого порядка не приписывают, это вообще, не алгебраическая поверхность.

Кривые 3-го и 4-го порядка

Описание: Первые рисунки на стенах пещер примитивные орнаменты на домашней утвари показывают что люди умели не только отличать прямую от кривой но и различать отдельные кривые. Впервые уравнение кривой исследовал Р. Оси координат служат касательными к ветвям кривой в начале координат поэтому кривая пересекает сама себя в начале координат под прямым углом. Вводя в качестве параметра отношение и подставляя в уравнение кривой легко получить параметрическое представление: В полярных координатах.

Дата добавления: 2015-07-25

Размер файла: 853.59 KB

Работу скачали: 204 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

СОДЕРЖАНИЕ

Глава I . Кривые 3-го порядка 3

§ 1. Декартов лист 4

§ 2. Циссоида Диоклеса 8

§ 3. Локон Аньези 16

Глава II . Кривые 4-го порядка 19

§ 1. Лемниската Бернулли 20

§ 3. Овалы Кассини 31

Список использованных источников 34

Понятие линии возникло в сознании человека в доисторические времена. Траектория брошенного камня, очертание цветов и листьев растений, извилистая линия берега и другие явления природы с давних пор привлекли внимание людей. Наблюдаемые многократно, они послужили основой для постепенного установления понятия о линии. Но потребовался значительный промежуток времени для того, чтобы наши предки стали сравнивать между собой формы кривых.

Первые рисунки на стенах пещер, примитивные орнаменты на домашней утвари показывают, что люди умели не только отличать прямую от кривой, но и различать отдельные кривые.

Так же и сегодня, все что нас окружает, состоит из множества черт, которые, в свою очередь, складываются из различных кривых.

Замечательные кривые обладают целым рядом геометрических и механических свойств. С ними связываются в истории математики ряд важных теоретических открытий. Поэтому знакомство с отдельными кривыми и их свойствами вызывает особый интерес, развивает математическое мышление, устанавливает связь математической теории с практикой.

С этой точки зрения моя работа посвящена вопросам замечательных кривых, описанию их замечательных свойств и особенностей формы отдельных кривых.

Кривые 3-го порядка

Кривые линии третьего порядка представляют собой геометрическое место точек, координаты которых в прямоугольной системе координат описываются алгебраическим уравнением третьей степени. Такие кривые могут иметь одну, две или три бесконечные ветви.

Среди большого разнообразия кривых третьего порядка существует ряд так называемых замечательных кривых, построения некоторых из них рассмотрим далее.

§ 1. Декартов лист

1.Исторические сведения. Впервые уравнение кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом координатном угле, где и принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. В то время эта кривая называлась цветком жасмина (рис. 1).

В современном виде эту кривую впервые представил Х. Гюйгенс в 1692 году.

2.Определение. Декартов лист плоская алгебраическая кривая третьего порядка. Ее уравнение в прямоугольной декартовой системе координат имеет вид

Параметр определяется как диагональ квадрата, сторона которого равна наибольшей хорде петли (рис. 2).

Прямая ось симметрии, её уравнение: .

Точка называется вершиной, её координаты

Для обеих ветвей существует асимптота , её уравнение: .

Оси координат служат касательными к ветвям кривой в начале координат, поэтому кривая пересекает сама себя в начале координат под прямым углом.

Вводя в качестве параметра отношение и подставляя в уравнение кривой легко получить параметрическое представление :

В полярных координатах декартов лист имеет вид (полюс,полярная ось)

Вычислим площадь петли декартова листа

От неявного задания кривой перейдем к заданию в полярных координатах

откуда, после сокращения на , получим

Так как петля кривой отвечает изменению от до , то искомая площадь равна

Вычислим площадь половины петли

и затем удвоим ее.

§ 2. Циссоида Диоклеса

1.Исторические сведения. Впервые циссоиду исследовал греческий математик Диокл во II веке до н. э. При этом древние греки рассматривали только часть циссоиды, лежащую внутри производящей окружности; эта часть циссоиды вместе с дугой окружности напоминают лист плюща.

Этим и объясняется название кривой: оно произошло от греческого слова χισσειδήζ плющевидный , похожий на лист плюща, которое, в свою очередь, пошло от χισσοζ плющ и ειδος вид, форма . Наличие бесконечных ветвей у циссоиды было установлено в 17 веке Робервалем и независимо от него Слюзом .

В современном виде циссоиду воспроизвел французский математик Жиль Роберваль в 1640 г.

2.Определение и построение кривой. Циссоида Диоклеса плоская алгебраическая кривая третьего порядка (рис. 3). Ее уравнение в прямоугольной декартовой системе координат имеет вид

Пусть Тогда, подставляя эти равенства в уравнение , получим

откуда, после сокращения на , получим уравнение циссоиды в полярной системе координат.

Уравнение циссоиды в полярной системе координат имеет вид (полюс,полярная ось):

В декартовой системе координат, где ось абсцисс направлена по , а ось ординат по , на отрезке строится вспомогательная окружность (рис. 4).

В точке проводится касательная . Из точки проводится произвольная прямая , которая пересекает окружность в точке и касательную в точке От точки, в направлении точки откладывается отрезок , длина которого равна длине отрезка

При вращении линии вокруг точки точка описывает линию, которая называется циссоида Диокла . Две ветви этой линии на рисунке показаны синим и красным цветами.

Асимптота:- радиус вспомогательной окружности.

Диокл строил кривую так: находится точка , которая расположена на вспомогательной окружности симметрично точке ; ось симметрии диаметр . Из точки проводится перпендикуляр к оси абсцисс.

Точка , принадлежащая циссоиде, находится на пересечении этого перпендикуляра и прямой .

Этим методом Диокл построил только кривую внутри вспомогательной окружности. Если эту часть циссоиды замкнуть дугой окружности , то получается фигура, напоминающая своей формой лист плюща, от чего и произошло название кривой.

I . Найдем площадь между кривой и асимптотой, используя формулу:

Итак, площадь, ограниченная циссоидой и ее асимптотой, равняется утроенной площади производящего круга

II . Найдем длину дуги кривой от точки до точки

Вернемся к и подставим полученное нами выражение:

Сначала вычислим неопределенный интеграл

Отдельно посчитаем интегралы:

III . Вычислим объем тела, образованного при вращении ветви вокруг оси абсцисс, используя следующую формулу:

1.Исторические сведения. Свое название кривая получила в честь итальянского математика Марии Гаэтаны Аньези (1718-1799), исследовавшей эту кривую (1748).Иначе эту кривую называют верзьерой.

Пьер Ферма в 1630 году нашёл площадь области между кривой и её асимптотой. В 1703 году Гвидо Гранди, независимо от Ферма, описал построение этой кривой, а в работе 1718 года назвал её верзьерой.

В 1748 году Мария Аньези опубликовала известный обобщающий труд «Основы анализа для итальянской молодежи», в котором кривая, как и в работе Гранди , именовалась верзьерой. По совпадению, итальянское слово Versiera/Aversiera, производное от латинского Adversarius, имело также значение «ведьма».

Возможно, по этой причине кембриджский профессор Джон Колсон , переводивший труд Аньези на английский, неправильно перевёл это слово, в результате чего в литературе на английском языке кривая часто именуется как «ведьма Аньези».

2.Определение и построение кривой. Локон Аньези плоская алгебраическая кривая третьего порядка, геометрическое место точек , для которых выполняется соотношение , где диаметр окружности, полухорда этой окружности, перпендикулярная .

В прямоугольной декартовой системе координат уравнение кривой имеет вид:

Параметрические уравнения кривой:

В полярной системе уравнение верзьеры достаточно сложное: чтобы найти его необходимо решить кубическое уравнение:

Однако полученная формула будет слишком сложной и громоздкой, чтобы иметь какое-либо практическое значение.

Ось абсцисс служит для кривой асимптотой. В точке локон и окружность имеют общую касательную, параллельную оси абсцисс.

Строится окружность диаметра и касательная к ней. На касательной выбирается система отсчёта с началом в точке касания. Строится прямая через выбранную точку касательной и точку окружности, противоположную точке касания. Эта прямая пересекает окружность в некоторой точке . Через эту точку строится прямая, параллельная касательной. Точка верзьеры лежит на пересечении этой прямой и перпендикуляра к касательной в выбранной точке.

I . Вычислим площадь между кривой и ее асимптотой, используя формулу:

Кривые 4-го порядка

Кривые линии четвертого порядка представляют собой геометрическое место точек, координаты которых в прямоугольной системе координат описываются алгебраическим уравнением четвертой степени.

Среди большого разнообразия кривых четвертого порядка существует ряд так называемых замечательных кривых, построения некоторых из них рассмотрим далее.

§ 1. Лемниската Бернулли

1.Исторические сведения. Название происходит от греч. λημνισχος (лемнискос) лента, повязка .

В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Данный вид лемнискаты назван в честь швейцарского математика Якоба Бернулли (1654-1705), положившего начало её изучению.

Уравнение лемнискаты впервые встречается в статье Я. Бернулли, опубликованной в 1694 г. в журнале «Труды ученых».

Он отмечает сходство этой линии с цифрой 8 и узлообразной повязкой, которую он именует «лемниском» (шерстяная повязка). Отсюда называние лемниската.

Лемниската получила широкую известность в 1718 г., когда итальянский математик Джулио Карло Фаньяно (1682 -1766) установил, что интеграл, представляющий длину дуги лемнискаты, не выражается через элементарные функции.

Некоторые свойства кривой были также исследованы Якобом Штейнером в 1835 году.

2.Определение . Лемниска́та Берну́лли плоская алгебраическая кривая 4-го порядка. Определяется как геометрическое место точек , произведение расстояний от которых до двух фиксированных точек (фокусов) и , отстоящих одна от другой на расстоянии есть величина постоянная.

Эта постоянная может выражаться любым положительным числом, заданием которого определяется квадрат половины расстояния между фиксированными точками (рис. 6).

Прямая ось лемнискаты. Точка , в которой лемниската пересекает саму себя, называется узловой точкой (или двойной) с касательными .

Касательные в двойной точке взаимно перпендикулярны.

Касательные к лемнискате, проведенные в концах хорды, проходящей через полюс системы, параллельны между собой.

В прямоугольной декартовой системе координат уравнение кривой имеет вид:

Уравнение кривой в полярной системе координат :

Если вместо подставить то уравнение не измениться. Отсюда следует, что кривая симметрична относительно полярной оси.

3.Построение кривой. Проведем прямую и отметим на ней точку . По обе стороны от данной точки построим два одинаковых отрезка равных . Так мы получим два фокуса лемнискаты

Затем, с центром в одном из фокусов, построим окружность радиуса . Далее, через точку проводится произвольная секущая где и -точки пересечения с окружностью (рис. 8).

После этого, от точки в обе стороны прямой откладываются отрезки равные хорде . Образовавшиеся точки и будут лежать на разных петлях лемнискаты (рис. 9).

Построив еще несколько секущих, мы определим больше точек, которые будут принадлежать лемнискате Бернулли (рис. 10).

Плавно соединив все точки, построенные на секущих, мы получим искомую кривую (рис. 11).

Так будет выглядеть лемниската (рис. 12).

I . Найдем площадь области, ограниченной лемнискатой (рис. 13), используя следующую формулу:

II . Вычислим длину дуги лемнискаты от вершины, отвечающей до любой точки с полярным углом , используя формулу:

Эта длина выражается эллиптическим интегралом 1-го рода. Так как таблицы вычислены для интегралов, в которых множитель при меньше единицы, то прибегаем к замене переменной.

Положим (так как , то и угол отсюда определить можно), тогда

Полагая, что а , для длины четверти лемнискаты получим выражение через полный эллиптический интеграл

Длина всей лемнискаты будет

4.Применение кривой. В технике лемниската используется, в частности в качестве переходной кривой на закруглениях малого радиуса, как это имеет место на железнодорожных линиях в горной местности и на трамвайных путях.

1.Исторические сведения. Кардиоида впервые встречается в трудах французского учёного Луи Карре (1705 г.). Название кривой дал Иоганн Кастильон (Джованни Франческо Мельчоре Сальвемини) в 1741 г.

Вычисление длины кривой, выполнил Ла Ир , который открыл кривую независимо, в 1708 г.

Также независимо описал кардиоиду голландский математик Й. Коерсма (1741). В дальнейшем к кривой проявляли интерес многие видные математики XVIII-XIX веков.

По мнению математиков, придумавших название кривой, она отдаленно напоминает форму сердца (греческое слово «кардиа» означает «сердце»).

2.Определение. Кардиоида плоская алгебраическая кривая 4-го порядка, которая описывается фиксированной точкой окружности радиуса , катящейся по неподвижной окружности с таким же радиусом (рис. 14).

В прямоугольной декартовой системе координат уравнение кривой имеет вид:

Выведем уравнение кривой в полярной системе координат:

Итак, уравнение кривой в полярной системе координат имеет вид

Подставляя в уравнения вместо уравнение кривой в полярных координатах, получим параметрические уравнения кривой

I . Найдем площадь всей кардиоиды.

То есть, мы получили, что площадь кардиоиды равна шестикратной площади основного круга.

II . Найдем длину всей кардиоиды, используя формулу:

То есть, мы получили, что длина кардиоиды равна восьмикратному диаметру основного круга.

3.Применение кривой. Кардиоида имеет различные применения в технике. В форме кардиоиды делают эксцентрики . Ею пользуются иногда при вычерчивании зубчатых колес.

Кардиоида хорошо знакома конструкторам и возникает при возвратно-поступательных движениях стержней в двигателях.

§ 3. Овалы Кассини

1.Исторические сведения. В 1680 г. знаменитый французский астроном Джованни Доменико (Жан Доменик) Кассини (1625-1712) начал изучать кривую, названную овалом Кассини . Он полагал, что линия, носящая теперь его имя, может точнее представить орбиту Земли, чем эллипс. Об этом стало известно в 1749 г. из публикации его сына Жака Кассини (тоже выдающегося астронома). Хотя гипотеза Кассини и не оправдалась, но введенная им линия стала предметом многочисленных исследований. Ее часто называют овалом Кассини, хотя на самом деле она не всегда овальна.

2.Определение. Овал Кассини — множество всех точек плоскости, для каждой из которых произведение расстояний до двух данных точек (фокусов) той же плоскости есть величина постоянная (рис. 15).

В прямоугольной декартовой системе координат уравнение кривой имеет вид:

Уравнение кривой в полярной системе координат :

В уравнении кривой содержатся два независимых параметра: половина расстояния между фокусами и произведение расстояний от фокусов до любой точки кривой.

В зависимости от величины параметров и различают три основные формы овалов Кассини, соответствующие трем соотношениям

Кривая в этом случае имеет форму замкнутой, симметричной относительно координатных осей линии (рис.15).

При таком соотношении параметров получается лемниската Бернулли, являющаяся, таким образом, частным случаем овалов Кассини (рис. 15).

Овал будет состоять в этом случае из двух замкнутых линий (рис. 15).

На этом очерк о замечательных кривых я заканчиваю. Я рассмотрела лишь немногие из них.

Применение замечательных кривых широко распространено, их применяют в производстве, строительстве. Замечательные кривые поистине замечательны своими свойствами. Трудно себе представить мир без этих кривых, хотя они так не заметны для нашего повседневного взора.

Несмотря на то, что у них на первый взгляд сложные и непонятные названия все они по-своему замечательные!

Видео:Поверхности 2 порядкаСкачать