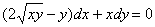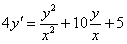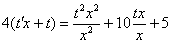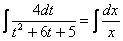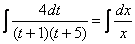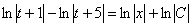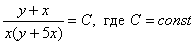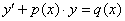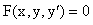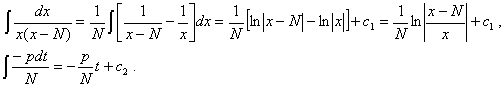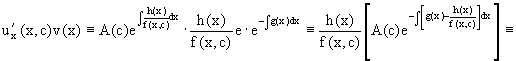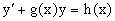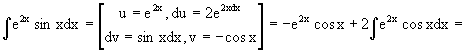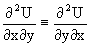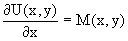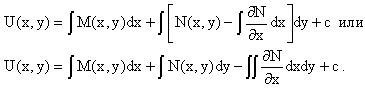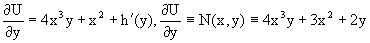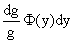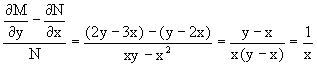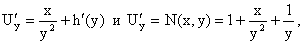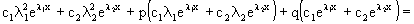В однородных уравнениях решение может потеряться в результате типовой замены и дальнейших сокращений, однако, на практике распространена и другая причина потери решений – это неосмотрительное деление. На самом деле с этим мы столкнулись в первом же примере вводного урока о дифференциальных уравнениях. В процессе решения уравнения 
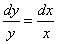
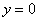

Аналогичная история с уравнением 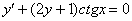



В действительности, конечно же, вовсе «не обошлось» – ситуация была под контролем, но я намеренно умолчал об этих нюансах на 1-ом уроке, чтобы не перегружать «чайников» информацией.
При неравносильных преобразованиях ВСЕГДА проверяйте (по крайне мере, устно), не теряете ли вы решения! Какие это преобразования? Чаще всего, сокращение на что-то или деление на что-то. Так, например, при делении на 
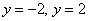

Перечисленные тонкости также теряют актуальность, если в задаче требуется найти только частное решение (см., например, Пример №2 первого урока).
Следующий диффур – самостоятельно:
Решить дифференциальное уравнение
Полное решение и ответ в конце урока. Попробуйте для тренировки и здесь выразить общее решение.
В заключительной части урока рассмотрим еще пару характерных задач по теме:
Решить дифференциальное уравнение
Решение: «любимая функция» 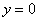
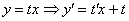
После замены проводим максимальные упрощения:
Разделяем переменные:

Интегрируем:
Интеграл левой части можно найти двумя способами: методом выделения полного квадрата или методом неопределенных коэффициентов. Как я уже отмечал, в диффурах удобнее использовать второй метод (если, конечно, многочлен можно разложить на множители)
Здесь многочлен на множители раскладывается: можно решить квадратное уравнение 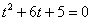
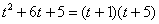
Методом неопределенных коэффициентов получим сумму дробей:


Таким образом:

Получившийся общий интеграл упрощаем:
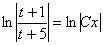
И только после упрощений выполняем обратную замену: 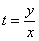
Ответ: общий интеграл:
Решить дифференциальное уравнение
Это пример для самостоятельного решения. Отмечу, что время от времени однородное уравнение встречается в виде дроби, и типичный пациент выглядит примерно так:
Наверное, многие обратили внимание, что во всех приведенных примерах мы не находили частные решения уравнений (задача Коши). Это не случайно. В практических заданиях
с однородными уравнениями частное решение требуют находить крайне редко, если честно, я даже не припомню таких случаев. Ну а если уж встретилась задача Коши в однородном уравнении, то, после изучения предыдущего урока, она не должна представлять для вас трудностей. Технология – точно такая же, как и для уравнений с разделяющимися переменными. Если уточнить, то почти всегда будут получаться не частные решения, а частные интегралы.
Существуют и более сложные однородные уравнения. Сложность состоит не в замене переменной или упрощениях, а в достаточно трудных или редких интегралах, которые возникают в результате разделения переменных. У меня есть примеры решений таких однородных уравнений – страшненькие интегралы и страшненькие ответы. Но о них не будем, иначе к большинству читателей во сне явится Александр Емелин известный персонаж с формулами на полосатом свитере.
И, для полноты картины, рекомендую изучить статью Линейные неоднородные дифференциальные уравнения.
Решения и ответы:
Пример 2: Решение: Проверим уравнение на однородность:
Вместо 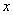
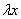

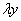

Все лямбды сократились, и получилось исходное уравнение, значит, данное ДУ является однородным.
Очевидно, что 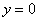
Проведем замену: 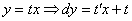
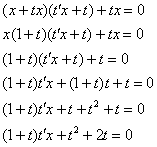
Разделяем переменные, слева собираем «тэ», справа – «иксы»:

Интегрируем:

Надо сказать, с интегралом левой части повезло, бывает гораздо хуже.
Максимально упрощаем общий интеграл.
Если есть дроби, то от них лучше избавиться, умножаем каждую часть на 2:

Константу 
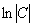

(Если этот момент не понятен, читайте статью Дифференциальные уравнения первого порядка)
Собираем в правой части всё под логарифм, затем избавляемся от логарифмов
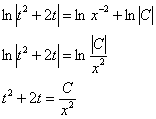
Обратная замена: 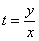

Умножаем все слагаемые на 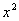

Ответ: общий интеграл:
Примечание: Решение 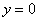
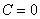
Проверка: Дифференцируем общий интеграл:
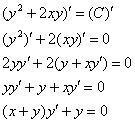
Получено исходное дифференциальное уравнение, значит, решение найдено верно.
Пример 4: Решение: Проверим уравнение на однородность:

Таким образом, данное уравнение является однородным.
Очевидно, что 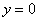
Проведем замену:
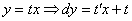

После подстановки проводим максимальные упрощения:

Разделяем переменные и интегрируем:

Новорожденный общий интеграл получен, здесь константу я не стал загонять под логарифм, в данном случае – это ни к чему. Использовать или не использовать этот прием с константой – понимание придет с опытом.
Упрощать особо нечего, поэтому проводим обратную замену: 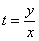

Общий интеграл можно упростить:

Ответ: общий интеграл: 
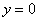
Примечание: здесь решение 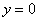
Пример 6: Решение: Преобразуем уравнение:
Очевидно, что 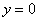
Данное уравнение является однородным, проведем замену:
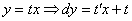

Максимально упрощаем:

Разделяем переменные и интегрируем:

Упрощать нечего, поэтому проводим обратную замену 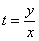

Ответ: общий интеграл: 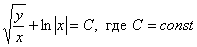
Примечание: также здесь можно выразить и общее решение: 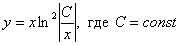
Пример 8: Решение: Данное ДУ является однородным, проведем замену: 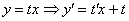
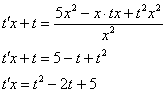



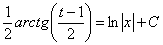
Обратная замена: 
Ответ: общий интеграл:
Линейные дифференциальные уравнения первого порядка.
Примеры решений
На данном уроке мы рассмотрим алгоритм решения третьего типа дифференциальных уравнений, который встречается практически в любой контрольной работе – линейные неоднородные дифференциальные уравнения первого порядка. Для краткости их часто называют просто линейными уравнениями. Материал не представляет особых сложностей, главное, уметь уверенно интегрировать и дифференцировать.
Начнем с систематизации и повторения.
На что в первую очередь следует посмотреть, когда вам предложено для решения любое дифференциальное уравнение первого порядка? В первую очередь необходимо проверить, а нельзя ли у данного диффура разделить переменные? Если переменные разделить можно (что, кстати, далеко не всегда очевидно), то нужно использовать алгоритмы и приемы решения, которые мы рассмотрели на первом уроке – Дифференциальные уравнения первого порядка. Советую посетить этот урок чайникам и всем читателям, которые чувствуют, что их знания и навыки в теме пока не очень хороши.
Если переменные в ДУ разделить не удалось, переходим к следующему этапу – проверяем, а не является ли уравнение однородным? Проверку обычно выполняют мысленно или на черновике, с самим алгоритмом проверки и образцами решения однородных уравнений можно ознакомиться на втором уроке – Однородные дифференциальные уравнения первого порядка.
Если переменные разделить не удалось, и уравнение однородным не является, то в 90% случаев перед вами как раз линейное неоднородное уравнение первого порядка.
Линейное уравнение первого порядка в стандартной записи имеет вид:
Что мы видим?
1) В линейное уравнение входит первая производная 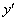
2) В линейное уравнение входит произведение 

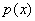
3) И, наконец, в линейное уравнение входит выражение 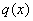
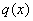
Примечание: Разумеется, в практических примерах эти три слагаемых не обязаны располагаться именно в таком порядке, их спокойно можно переносить из части со сменой знака.
Перед тем, как перейти к практическим задачам, рассмотрим некоторые частные модификации линейного уравнения.
– Как уже отмечалось, выражение 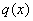

– Выражение 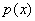

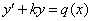


– Рядом с производной может находиться множитель 

Решить дифференциальное уравнение
Решение: Данное уравнение является линейным и имеет простейший вид: 
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Особые решения дифференциальных уравнений
Решение дифференциального уравнения
называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению
Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).
Полученное после исключения из (1) и (2) уравнение
Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.
Пример 1. Найти особые решения дифференциального уравнения
а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем
Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.
б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).
в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение
Выпишем условие касания двух кривых и в точке с абсциссой :
Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .
Полагая , находим, что условия (7) принимают вид
Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.
Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).
г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).
Огибающей семейства кривых
называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.
Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.
Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.
Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений
Некоторая ветвь СДК заведомо будет огибающей, если на ней:
1) существуют ограниченные по модулю частные производные
где и — постоянные;
Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.
Пример 2. Найти особые решения дифференциального уравнения
а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда
Это и есть C-дискриминантная кривая: она состоит из двух прямых и .
б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).
в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке
где — область допустимых значений .
Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).
Итак, установлено, что каждое из решений (15) есть особое решение.
В вопросах отыскания особых решений оказываются полезными следующие символические схемы:
Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места точек заострения (возврата);
3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.
Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:
1) — уравнение огибающей;
2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;
3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.
Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).
Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.
В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.
Пример 3. Найти особое решение дифференциального уравнения
Решение. Особое решение, если оно существует, определяется системой
где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви
Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).
Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства
являющегося общим интегралом для (18).
Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.
Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).
Пример 4. Найти особые решения дифференциального уравнения
Решение. Дифференцируем (23) по
Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.
Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).
Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).
Пример 5. Найти особые решения дифференциального уравнения
Решение. Найдем . Исключая из системы уравнений получаем
Преобразовав уравнение (25) к виду , находим его общий интеграл .
Найдем . Исключая из системы уравнений будем иметь
Итак, из (26) и (27) имеем
Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.
Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .
Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).
Пример 6. Найти особые решения дифференциального уравнения
а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда
Подставляя (29) в (28), найдем уравнение :
б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде
Дифференцируя обе части (28) по и учитывая, что , будем иметь
Приравнивая нулю первый множитель , получаем (29), а соотношение дает
Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):
в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь
Подставляя (34) в (33), получаем уравнение .
Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Особые решения дифференциального уравнения
2. Особые решения дифференциального уравнения.
Пусть рассматривается дифференциальное уравнение первого порядка общего вида F(x,y,y/)=0.
Тогда существование его особого решения прежде всего может быть связано с условием 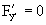
Таким образом, формируя систему уравнений
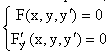
и исключая из нее переменную y/, получаем функцию y=y(x), которая может дать особое решение дифференциального уравнения F(x,y,y/)=0.
Определение. Кривая, получаемая исключением параметра p из системы уравнений
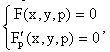
называется дискретной кривой уравнения F(x,y,y/)=0.
Для того, чтобы дискретная кривая давала особое решение дифференциального уравнения, остается проверить, что она удовлетворяет уравнению F(x,y,y/)=0, и что через каждую ее точку проходит хотя бы одна интегральная кривая общего решения этого уравнения, т.е. проверить, что в точках дискретной кривой нарушается свойство единственности решения дифференциального уравнения.
Пример 1. Дано уравнение 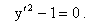
Как было указано выше его особое решение дается уравнениями y=x+c и y=-x+c. Опреляя для него дискретную кривую имеем систему уравнений
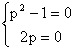
Очевидно, данная система решения не имеет, поэтому рассматриваемое дифференциальное уравнение особых решений не имеет.
Пример 2. Рассмотрим решение уравнения
Его общее решение имеет вид 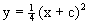
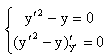
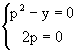
и исключая из нее переменную p, получаем уравнение дискретной кривой y=0 (ось Ox). Очевидно, она является решением дифференциального уравнения, так как из y=0=const следует y/=0. Кроме того через любую точку M(x0;0) этой кривой проходит частное решение дифференциального уравнения, получаемое из общего при c=-x0. Не трудно убедиться, что касательные в точке M(x0;0) дискретной кривой и частного решения совпадают. Таким образом, дискретная кривая y=0 является особым решением исходного дифференциального уравнения.
Ниже на рис. 3 изображено семейство интегральных кривых этого уравнения, являющееся семейством парабол.
Из рисунка видно, что дискретная кривая y=0, являющаяся осью Ox, касается в каждой точке некоторой кривой семейства.
Выше была рассмотрена ситуация, когда уравнение F(x,y,y/)=0 не определяло y/ как неявную функцию переменных x и y, так как выполнялось условие 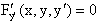
Предположим теперь, что в области D, где ищется решение дифференциального уравнения, выполняется условие 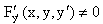
Таким невыполнимым условием, обычно, берется условие Липшица, и геометрическое место точек, в которых оно нарушается, задается условием 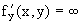
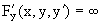
Пример 3. Рассматривается дифференциальное уравнение 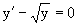
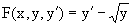
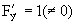
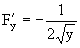
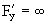
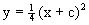
Пример 4. Дано уравнение 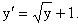
Для него 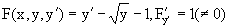
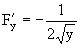
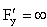
Однако, в данном случае кривая y=0 не удовлетворяет дифференциальному уравнению. Следовательно, это уравнение особых решений не имеет.
Особым решением дифференциального уравнения довольно часто бывают огибающие семейства его интегральных кривых.
Определение. Кривая y=y(x) называется огибающей семейства интегральных кривых интегрального уравнения, задаваемого общим решением Ф(x,y,c)=0, если в каждой точке она касается одной из кривых данного семейства, т.е. имеет с ней в этой точке общую касательную.
Для нахождения огибающей может быть использован следующий подход.
Пусть огибающая задана параметрически уравнениями x=x(t),y=y(t).
Со значением параметра t можно связать значение постоянной c, отвечающей той интегральной кривой семейства Ф(x,y,c)=0, которая касается огибающей в точке M(x(t),y(t)), т.е. величину c можем рассматривать как функцию параметра t, а именно c=c(t).
Подставляя функции x=x(t),y=y(t) и c=c(t) в Ф(x,y,c)=0, получаем тождество
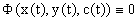
Предполагая, что Ф(x,y,c) имеет непрерывные частные производные первого порядка, из тождества вытекает 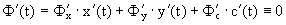
Покажем, что 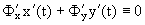
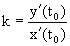
Уравнение Ф(x,y,c0)=0, где c0=c(t0), задает интегральную кривую семейства, проходящую через точку M0(x0, y0). Угловой коэффициент касательной к данной интегральной кривой в точке M0(x0, y0) равен 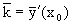
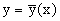
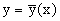
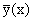
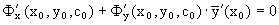
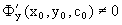
Из 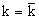
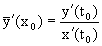
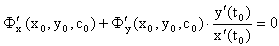
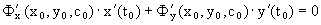
Таким образом, для произвольного значения t0 параметра t выполняется 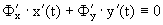
Следовательно, из 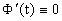
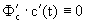
Но так как 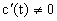
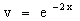
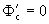
Таким образом, для нахождения огибающей надо рассмотреть систему уравнений
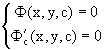
Исключая из нее параметр c, найдем уравнение y=y(x) или Y(x,y)=0 огибающей (исключая точки, где одновременно 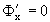
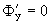
Пример 5. Снова рассмотрим уравнение из примера 2 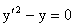
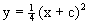
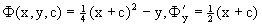
Для нахождения огибающей рассмотрим систему
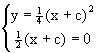
Из нее получаем уравнение огибающей y=0. Далее убеждаемся, что y=0 действительно является огибающей, так как через каждую ее точку M(x0;0) проходит интегральная кривая со значением параметра c=-x0.
Пример 6. Рассмотрим дифференциальное уравнение 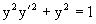
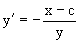
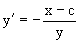
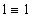
Нетрудно видеть, что семейством интегральных кривых являются окружности единичного радиуса с центром в точках (c,0), лежащих на оси Ox.
На рис. 4 изображено семейство этих окружностей.
Из рисунка видно, что семейство интегральных кривых имеет две огибающие y=1 и y=-1, удовлетворяющих диффренциальному уравнению и, следовательно, дающих его два особых решения.
Найдем уравнения огибающих аналитически. Из Ф(x,y,c)=(x-c)2+y2-1, 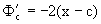
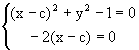
Исключая из уравнения параметр c, получаем y2=1. Данное уравнение дает две огибающих y=1 и y=-1.
Пример 7. Дано уравнение 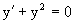
Его общее решение будет 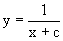
Из 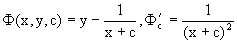
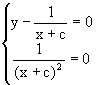
Исключая из уравнений параметр c получаем уравнение кривой y=0, являющейся осью Ox.
Кривая y=0 удовлетворяет дифференциальному уравнению и, следовательно, является его решением. Однако, она не является огибающей, так как не имеет общих точек с интегральными кривыми семейства. Таким образом, являясь решением уравнения, она не является его особым решением.
Далее будут рассмотрены методы решения отдельных типов дифференциальных уравнений.
3. Дифференциальное уравнение первого порядка с разделяющимися переменными.
Определение. Дифференциальное уравнение первого порядка
называется уравнением с разделяющимися переменными, если оно может быть представлено в виде 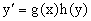
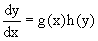
Разнося переменные x и y и их дифференциалы в разные стороны такого уравнения, оно может быть записано в виде
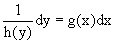
Можно следующую интерпретацию происхождения данного уравнения.
Пусть величина Z является с одной стороны функцией величины y, т.е. z=M(y). С другой стороны величина Z является функцией величины x, т.е. z=g(x). Например, если Z-объем выпуска продукции, то с одной стороны z зависит от величины y – объема основных фондов, с другой стороны z может рассматриваться зависимой от величины x – объема затрачиваемых трудовых ресурсов. Таким образом, через соотношения z=H(y) и z=G(x) одна из величин y или x представляется функцией другой величины x или, соответственно, y. Исходное дифференциальное уравнение отображает эту функциональную связь через дифференциалы функций H(y) и G(x), уравнивая их, т.е. dz=dH(y)=dG(x). Отсюда можно считать, что 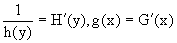
Таким образом, чтобы найти эту функциональную связь в виде y=y(x),x=x(y) или f(x,y)=0, надо проинтегрировать каждую из частей дифференциального уравнения, получая
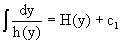
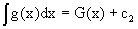
Если это возможно, из него одна из величин может быть представлена явно функцией другой y=y(x) или x=x(y).
Пример 1. Рассмотрим дифференциальное уравнение получаемое при моделировании процесса распространения информации о новом товаре
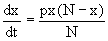
Данное уравнение, очевидно, относится к уравнению с разделяющимися переменными. Разнеся переменные x и t и их дифференциалы по разные стороны, уравнение запишем в виде
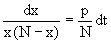
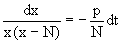
Проинтегрируем каждую из сторон этого уравнения:
Приравнивая найденные интегралы получаем
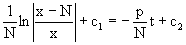
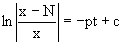
где c=N(c1-c2). Отсюда далее 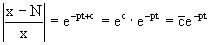
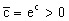
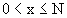
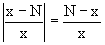
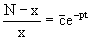
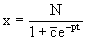
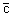
Нетрудно проверить, что дискретной и огибающей кривых дифференциальное уравнение не имеет. Однако беря крайние значения для 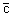
Пример 2. Возьмем дифференциальное уранение
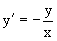
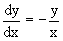
геометрическая иллюстрация решений которого рассматривается в параграфе 2.
Данное уравнение является с разделяющимися переменными> Разнося переменные в разные стороны, записываем уравнение в виде
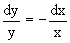
Интегрирование левой и правой частей уравнения, дает общее решение вида 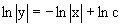
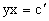
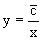
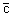
Как видно получилось семейство гипербол.
Пусть из данного семейства интегральных кривых (гипербол) необходимо выделить кривую (решение) проходящую через точку M(1,1), т.е. выделить решение, удовлетворяющее начальному условию y(1)=1. Для этого в общее решение уравнения подставим значения x=1, y=1, и найдем, отвечающее искомой кривой, значение постоянной 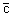
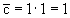
Yx=1 или 
Пример 3. Рассмотрим уравнение 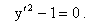
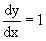
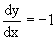
Оба являются с разделяющимися переменными и приводятся к виду dy=dx и dx=-dx. Интегрирование левых и правых частей уравнений дает следующие их общие решения y=x+c и y=-x+c.
Пример 4. Следующим уравнением возьмем уарвнение 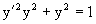
Разрешая его относительно y/ получаем
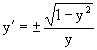
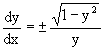
Разделяя переменные имеем
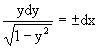
Найдем интегралы от левой и правой частей уравнения:
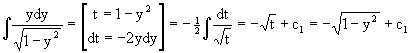
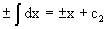
Приравнивая интегралы и заменяя две постоянных на одну получаем следующий вид общего решения уравнения
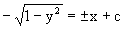
Возводя в квадрат обе части данного уравнения, получаем окончательный вид общего решения
Пример 5. Решить дифференциальное уравнение 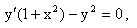
Найти его частное решение при условии 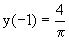
Разрешая уравнение относительно y/, видим, что оно является уравнением с разделяющимися переменными
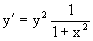
Разнося переменные по разные стороны уравнения получаем
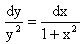
Интегрируя каждую из частей этого уравнения, получаем следующее общее решение исходного дифференциального уравнения
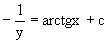
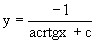
Используя начальное условие 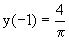
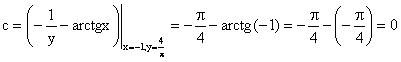
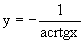
4. Однородное дифференциальное уравнение первого порядка.
Функция f(x,y) называется однородной степени m, если 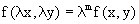
Функция f(x,y) называется однородной нулевой степени, если 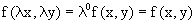
Например, функция 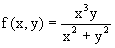
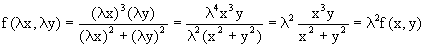
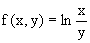
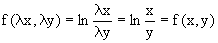
Всякая однородная функция нулевой степени может быть представлена в виде функции от отношения y/x (или отношения x/y). Действительно, пусть f(x,y) – однородная функция нулевой степени, тогда, взяв в качестве 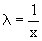
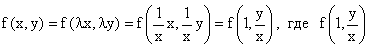
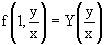
Определение. Дифференциальное уравнение первого порядка F(x,y,y/)=0, называется однородным, если оно может быть представлено в виде y/=f(x,y) или 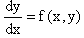
Решение однородного дифференциального уравнения сводится к решению уравнения с разделяющимися переменными заменой y/x=u или y=ux, где u-функция от x.
Подставляя в исходное уравнение 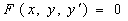
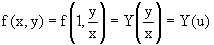
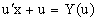
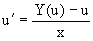
Пример 1. Рассматривается уравнение
Перепишем его в виде 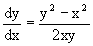
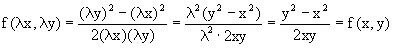
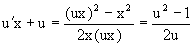
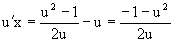
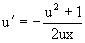
Разделяя переменные приходим к уравнению
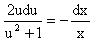
Интегрируем левую и правую части этого уравнения:
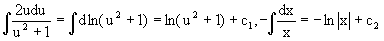
Приравнивая найденные интегралы, получаем общее решение вспомогательного дифференциального уравнения относительно переменных x и u
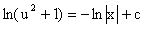
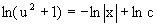
Потенциируя последнее выражение, общее решение получает вид 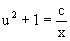
Заменяя u=y/x, получаем общий интеграл исходного дифференциального уравнения 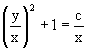
Последнее выражение приводится к виду
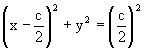
Таким образом, семейством интегральных кривых исходного уравнения является семейство окружностей с центрами в точках 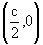
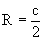
Пример 2. Требуется найти частное решение уравнения 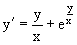
Удовлетворяющих начальному условию y(1)=0.
Нетрудно видеть (убедиться), что справа стоит однородная функция нулевой степени. Итак, исходное дифференциальное уравнение является однородным. Выполняя замену y=ux, приводим его к виду
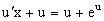
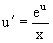
Разделяем переменные, получаем
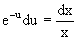
Интегрируя обе части этого уравнения, получаем общее решение вспомогательного дифференциального уравнения
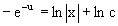
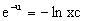
Подставим в него 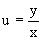
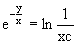
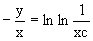
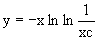
Последнее соотношение дает общее решение исходного дифференциального уравнения. Чтобы найти частное решение, воспользуемся начальными условиями x=1,y=0. Подставим их в общее решение 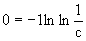
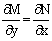
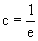
Таким образом, искомое частное решение имеет вид 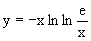
5. Линейное дифференциальное уравнение первого порядка.
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x).
Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное.
Если 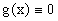
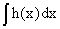
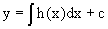
Если 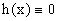
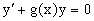
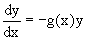
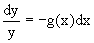
Его общее решение имеет вид 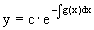
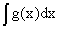
Предположим теперь, что 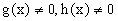
Представим исходное уравнение в виде
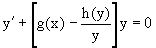
и подставим в выражение, стоящее в квадратных скобках, 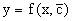
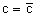
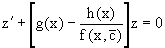
являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным).
Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде
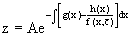
где A – произвольная постоянная. Очевидно, 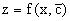
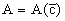
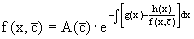
Если теперь освободиться от условия фиксирования постоянной 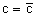
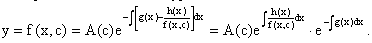
В нем второй множитель функция 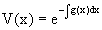
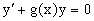
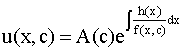
Действительно, подставляя в это уравнение u/x(x,c), получаем тождество
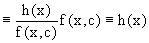
Таким образом, показано, что общее решение линейного дифференциального уравнения
Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного уравнения 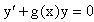
Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными.
Заметим, что хотя при решении однородного уравнения 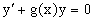
Являющегося уравнением с разделяющимися переменными.
На втором этапе определяется решение u(x,c) дифференциального уравнения u/v(x)=h(x),
Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде
Пример 1. Решить уравнение
Сначала решаем однородное уравнение v/+2v=0.
Из него получаем
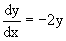
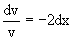
Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида
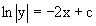
Полагая в нем c=0 и потенциируя его, получаем следующее его нетривиальное частное решение 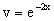
Далее решаем уравнение вида
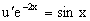
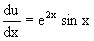
Разнося переменные в разные части уравнения и интегрируя их, получаем общее решение этого уравнения
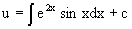
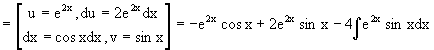
Рассматривая данное уравнение, как уравнение относительно интеграла, находим его вид
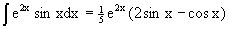
Следовательно, 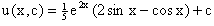
Тогда общее решение исходного уравнения будет
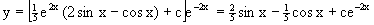
Предположим теперь, что требуется выделить частное решение, проходящее через точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для этого подставим значения x=0, y=0 в общее решение и найдем соответствующее значение постоянной c:
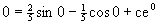
Искомым частным решением является
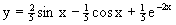
Пример 2. Решить уравнение
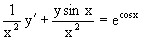
являющееся линейным дифференциальным уравнением.
На первом этапе найдем решение соответствующего линейного однородного уравнения

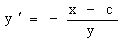
Разделяя переменные по разные стороны уравнения, имеем
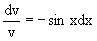
Интегрируя обе части данного уравнения, получаем следующее его частное решение
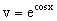
На втором этапе решаем уравнение вида
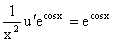
Делая замену 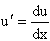
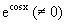
Интегрируя правую и левую части уравнения, получаем его общее решение
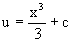
Общее решение исходного дифференциального уравнения имеет вид
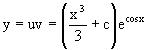
6. Дифференциальное уравнение первого порядка в полных дифференциалах.
Определение. Пусть дифференциальное уравнение первого порядка представлено в виде
Где M(x,y) и N(x,y) – функции двух переменных x и y. Тогда, если левая часть уравнения есть полный дифференциал некоторой функции U(x,y), т.е.
то такое уравнение называется уравнением в полных дифференциалах.
Уравнение в полных дифференциалах кратко можно представить в виде
а поэтому общий интеграл (решение) такого уравнения имеет вид U(x,y)=0.
Дифференциальное уравнение такого типа возникает, когда поведение системы подчинено условию сохранения некоторой величины U(энергии, массы, стоимости и т.д.).
Отметим следующий признак, позволяющий определить является ли рассматриваемое уравнение уравнением в полных дифференциалах.
dU(x,y)=M(x,y)dx+N(x,y)dy, тогда функции M(x,y) и N(x,y) должны быть для U(x,y) частными производными первого порядка, соответственно, по переменным x и y, т.е.
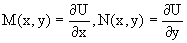
Предполагая функции M(x,y) и N(x,y) непрерывными и имеющими непрерывные частные производные, соответственно, по y и x, т.е. выполнение соотношений
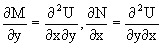
получаем, что для M(x,y) и N(x,y) должно выполняться условие
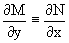
Полученное условие является не только необходимым, но и достаточным для того, чтобы уравнение M(x,y)dx+N(x,y)dy=0
Было уравнением в полных дифференциалах.
Нахождение общего решения уравнения в полных дифференциалах проводится в два этапа.
На первом этапе функция U(x,y) рассматривается как функция только аргумента x, переменная y получает как бы фиксированное значение 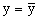
ставится в соответствие дифференциальное уравнение
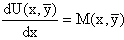
Пусть его общее решение представляется в виде
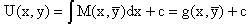
Но так как решение уравнения зависит от y, то в общем решении постоянная c является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего дифференциального уравнения, снимая с y условие закрепления его значения, имеет вид
На втором этапе находится вид функции h(y). Для этого обратимся к соотношению
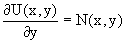
в котором уже закрепляется как бы значение переменной x.
Используя данное соотношение и вид функции U(x,y), получаем дифференциальное уравнение, связывающее переменные h и y:
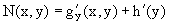
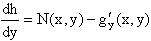
Интегрируя это уравнение, находим его общее решение
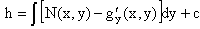
Из 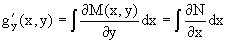
В последнем двойном интеграле вместо 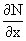
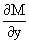
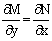
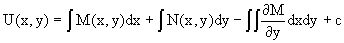
Так как общее решение исходного дифференциального уравнения записывается в виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий вид общего решения уравнения
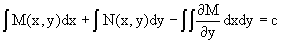
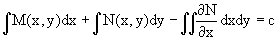
Пример 1. Дано дифференциальное уравнение
В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из 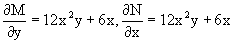
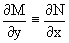
Следует, что данное уравнение является уравнением в полных дифференциалах. Проведем его решение в два этапа.
На первом решаем уравнение
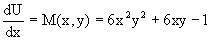
в котором переменная y считается закрепленной. Интегрируя это уравнение, получаем
На втором этапе определяем вид функции h(y), используя для этого соотношение
и дифференциальное уравнение для h и y
4x3y+3×2+h/(y)=4x3y+3×2+2y или 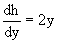
Интегрируя последнее, получаем h=y2+c. Общий интеграл исходного уравнения тогда можно записать в виде
Пример 2. Найти решение уравнения
Проверяем, является ли оно уравнением в полных дифференциалах? Для этого из M(x,y)=2xsiny, N(x,y)=3y2+x2cosy
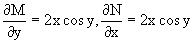
Так как, очевидно, выполняется условие
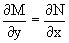
то уравнение есть уравнение в полных дифференциалах.
Сначала решаем уравнение
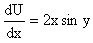
считая y постоянной. Интегрирование уравнения дает
Затем находим функцию h(y), используя соотношения
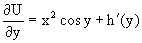
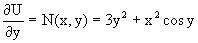
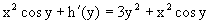
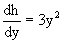
Интегрируя последнее уравнение, получаем h=y3+c.
Тогда общий интеграл исходного дифференциального уравнения записывается в виде
Далее рассмотрим понятие интегрирующего множителя. Ранее отмечалось, что уравнение в полных дифференциалах возникает, когда поведение системы сохраняет некоторую величину U, т.е. удовлетворяет соотношению
Дифференциальным аналогом его является уравнение dU(x,y)=0 или
Где 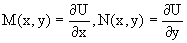
Предположим теперь, что частные производные функции U(x,y) представимы в виде
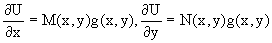
Тогда соотношению U(x,y)=e будет соответствовать уравнение в полных дифференциалах вида
Если теперь данное уравнение разделить на общий множитель слагаемых g(x,y), то получим уравнение M(x,y)dx+N(x,y)dy=0.
Решение последнего уравнения эквивалентно решению предыдущего, из которого оно получено, однако оно может уже не являться уравнением в полных дифференциалах, также для него возможно будет
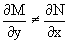
В то же время после умножения его на множитель g(x,y), оно становится уравнением в полных дифференциалах.
Определение. Функция g(x,y) называется интегрирующим множителем дифференциального уравнения
Если после умножения его на эту функцию оно становится уравнением в полных дифференциалах.
Данный способ решения дифференциального уравнения называется методом интегрирующего множителя.
Найдем условие, которому должен подчиняться интегрирующий множитель g(x,y). Из предложения, что уравнение
Становится уравнением в полных дифференциалах следует выполнение условия
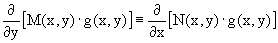
Разверернув левую и правую части этого тождества
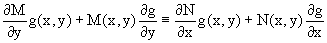
заключаем, что функция g(x,y) должна являться решением уравнения
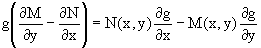
В общем случае решение данного уравнения вызывает затруднения. Отметим два случая, когда его решение становится проще.
Случай первый. Пусть
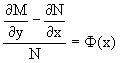
Тогда интегрирующий множитель можно искать в виде функции зависящей только от x.
Действительно, пусть g=g(x). Тогда в виду 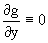
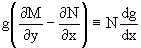
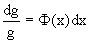
интегрируя которое, находим
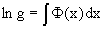
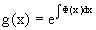
Второй слуяай относится к аналогичной ситуации, когда
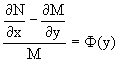
Тогда интегрирующий множитель ищется в виде функции только от y, т.е. g=g(y).
Аналогично предыдущему, не трудно видеть, что функция g(y) является решением уравнения
и представляется в виде
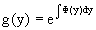
Пример 3. Дано уравнение
Из M(x,y)=y2-3xy-2×2, N(x,y)=xy-x2, 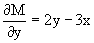
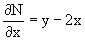
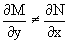
Однако из соотношения
вытекает, что можно найти такой интегрирующий множитель g=g(x), после умножения на который исходное уравнение становится уравнением в полных дифференциалах.
Указанный множитель находим из уравнения
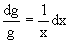
интегрируя которое получаем 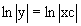
Умножая исходное уравнение на множитель g=x, получаем
являющееся уже уравнением в полных дифференциалах. Интегрируя его, находим
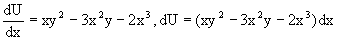
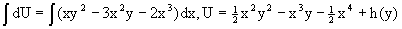
затем из U/y=x2y-x3+h/(x) и U/y=N(x,y)=x2y-x3
получаем x2y-x3+h/=x2y-x3, т.е. 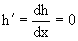
следовательно, h=c=const. Таким образом, общее решение имеет вид
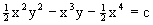
Пример 4. Требуется решить уравнение
Из M(x,y)=2xy2-y, N(x,y)=y2+x+y, 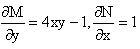
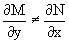
Однако из соотношения
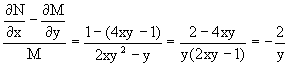
вытекает, что для исходного дифференциального уравнения существует интегрирующий множитель g=g(y), с помощью которого уравнение становится уравнением в полных дифференциалах.
Интегрирующий множитель находится из уравнения
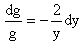
Интегрируя его, получаем 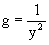
Умножая исходное уравнение на множитель 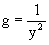
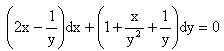
Это уравнение является уже уравнением в полных дифференциалах. Решаем его
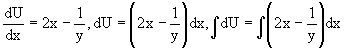
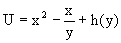
затем из
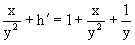
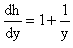
Интегрируя последнее уравнение, имеем 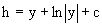
Таким образом, общий интеграл исходного уравнения имеет вид
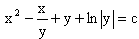
7. Дифференциальные уравнения второго порядка.
Обыкновенное дифференциальное уравнение второго порядка имеет следующий общий вид
F(x,y,y/,y//)=0 или 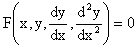
Наше знакомство с дифференциальными уравнениями второго порядка будет ограничено рассмотрением линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где p и q – числа, h(x) – некоторая функция от x.
Если в этом уравнении 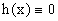
Рассмотрим решение однородного уравнения
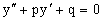
Этому явлению может быть поставлено в соответствие квадратное уравнение вида 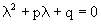
Называемое характеристическим. Его корни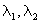
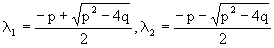
Возможны следующие три случая для вида корней 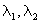
1) корни уравнения – действительные и различные;
2) корни – действительные и равные;
3) корни уравнения – комплексно-сопряженные.
Для каждого из этих случаев однородное дифференциальное уравнение имеет свой вид общего интеграла.
Случай 1. Дискриминант характеристического уравнения положителен, т.е. p2-4q>0. Тогда оба корня 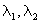
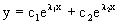
где c1, c2 – произвольные постоянные.
Действительно, если 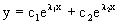
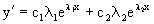
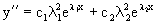
Подставляя выражения для y,y/ и y// в уравнение получим
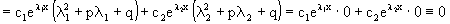
Случай 2. Дискриминант характеристического квадратного уравнения равен нулю, т.е p2-4q=0.
Тогда оба корня 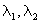
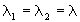
В этом случае общее решение однородного уравнения имеет вид
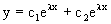
🎥 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

6. Особые решения ДУ первого порядкаСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать
Общее и частное решение дифференциального уравненияСкачать
Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения. 11 класс.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Задача Коши для дифференциальных уравненийСкачать

Как распознать талантливого математикаСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

11. Уравнения в полных дифференциалахСкачать