Пример 15. Построим множество точек ( x , y ) (x, y) , удовлетворяющих уравнению x 2 + x y = 0 x^2 + xy = 0 .
Построим множество точек ( x , y ) (x, y) таких, что
x 2 + 4 x + 4 + 4 y 2 = 0 x^2 + 4x + 4 + 4y^2 = 0 .
Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.
т. е. уравнению снова будет удовлетворять единственная точка ( 0,5 ; – 0,5 ) (0,5; – 0,5) (см. рис. 39).
Множеством точек может быть область на плоскости. Рассмотрим пример.
Построим множество точек ( x , y ) (x, y) таких, что
Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.
Построим множество точек, удовлетворяющих | y | = | x | |y| = |x| .
- Графики функций, содержащих знак модуля (стр. 2 )
- Найти множество точек координатной плоскости удовлетворяющих уравнению x ^ 2 + y ^ 2 — 6x + 2y = 6?
- Решите пожалуйста подробно?
- Постройте множество на координатной плоскости, задаваемое неравенством|x| + 3|y|< ; 6?
- Построить на плоскости множество точек, координаты которых удовлетворяют равенству 4у2 — 2х2 — 1 = |4х2 — 2у2 — 1|?
- Найти множество точек координатной плоскости, удовлетворяющих уравнению : 1) х + у — 3 = 0 2)( х — 3) ^ 2 + (y + 2) ^ 2 = 16?
- Изобразите на координатной прямой множество точек, координаты которых удовлетворяют двойному неравенству ; б) — 15< ; х< ; 27?
- Нарисовать любой рисунок координатной плоскости из 20 точек на координатной плоскости?
- На координатной плоскости покажите штриховкой множество точек, заданных системной неравенств : ( » ^ » — в квадрате) y≥x ^ 2 y — 4≤0?
- СРОЧНО?
- 2. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию : а) х = — 2 ; б) у = 4?
- На координатной плоскости закрасьте множество точек (х, у)?
- 🌟 Видео
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Графики функций, содержащих знак модуля (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |




 |  |

 |
Рис.9 -3 У=2│х│-3 Рис.10
При решении девятого задания, рассмотрим цепочку функций: у1=│х +2│, у2 =│х +2│-3 и у=││х+2│-3│). Графики первых двух мы умеем строить (первый изображён тонкой сплошной линией, а второй – сплошной жирной и частично пунктирной линией). При построении третьего достаточно отразить нижнюю часть второго графика зеркально относительно оси абсцисс (на рис.10 эта часть показана сплошной линией).
Для закрепления навыков построения графиков функций, содержащих модули, выполните самостоятельно следующие задания, а потом проверьте свои чертежи с рисунками 11 – 13.
№ 3. Построить графики функций:
10) у = – │х – 3│, 11) у = -3│ х│+5, 12) у = 0,5│х — 2│- 4.
 |  |











Рис.11 Рис.12 Рис.13
В тестах часто встречаются некоторые примеры, использующие функции и графики специфического вида. И хотя эти функции и не входят в общую программу, но лучше знать основные особенности некоторых «полезных» функций и их графики. Такие графики могут встретиться на математических олимпиадах, абитуриентам на вступительных экзаменах. Знание этих функций, умение быстро построить график позволяет ускорить решение многих примеров. Для запоминания удобно дать этим графикам «имена».
№4. Построить графики функций:
13) у = │х — а│+│х — в│ («Корыто»);
14) у = │х — а│-│х — в│ («Ступенька»);
15) у = ││х — а│ — в│ («W»). Эта функция нам уже встречалась.
Рассмотрим график под номером 13 (рис. 14) в общем виде

Например, построим график функции: У=│х-1│+│х+2│.
 |
 |







Рассмотрим график под номером 15 (рис. 18) в общем виде
 |  |

Задания для самостоятельного решения.
№ 5. Используя переход к блочно-кусочному виду, постройте графики следующих функций:
16) у = │х +1│-│х -1│, 17) у =│-│х + 3│ — 2│,
18) у = │х -1│-│х + 1│, 19) у = │х│- х, 20) у = │1-х│-│х-2│-│х-3│,
Геометрическое место точек вида │у│=│х│, │у –у0│=│х – х0│ и других.
Мы рассмотрели наиболее общие методы построения графиков некоторых функций вида у = f(x). При этом каждому допустимому значению аргумента соответствовало одно значение функции. Однако на практике очень часто встречаются такие зависимости между двумя переменными х и у, в которых одному значению х соответствует два или более значений у. Зависимость между двумя переменными может быть задана и в виде неравенства. Подобные зависимости тесно связаны с понятием геометрического места точек.
Определение. Геометрическим местом точек, обладающих каким-либо свойством, называется множество, в которое входят все те и только те точки, которые обладают этим свойством.
Указанное в данном определении свойство, характеризующее геометрическое место точек (г. м.т.) может задаваться либо уравнением вида F(x;y) = 0, либо неравенством F(x;y) ≥ 0.
Например, г. м.т., координаты которых удовлетворяют уравнению х2+ у2= 1,
является окружность единичного радиуса с центром в начале координат. Г. м.т., координаты которых удовлетворяют неравенству х2 + у 2≤ 1, будет круг единичного радиуса с центром в начале координат. Каждому значению х из интервала -1≤х≤1 в первом случае соответствует два значения, во втором случае – бесконечное множество значений у.
Все графики функций у= f(x), которые рассматривались до сих пор, можно также рассматривать как геометрические места точек, координаты которых удовлетворяют заданному уравнению у= f(x). Таким образом, построение г. м.т., координаты которых удовлетворяют какому-либо соотношению, является задачей более общей, чем построение графиков (однозначных) функций. Г. м.т. плоскости, когда каждому значению аргумента х соответствует не одно, а два или более значений переменной у, называют многозначной функцией.
В настоящем параграфе рассмотрим ряд заданий, посвящённых отысканию на плоскости ХОУ геометрических мест точек, координаты которых удовлетворяют заданному уравнению F(x;y) = 0 или неравенству F(x;y) ≥ 0.

Заметим попутно, что при построении геометрических мест точек такого вида (да и любых других) полезно использовать чётность по одной или двум координатным осям. Это экономит время при выполнении заданий.
Изобразите в плоскости ХОУ множество всех точек, координаты которых удовлетворяют равенству ││х│ -│у││=1.
Выражение чётно по двум координатным осям, поэтому достаточно провести построение лишь при х ≥ 0, у ≥ 0, т. е. в первом квадранте, где уравнение имеет вид │х — у│= 1. Последнее выражение эквивалентно двум уравнениям х – у = 1 и х – у = — 1, определяющим две параллельные прямые, построение которых и произведём (с учётом ограничения выполняем построение только двух лучей, расположенных в первом квадранте). Далее, используя чётность (проведя отражения относительно осей координат), получим искомое геометрическое место точек (рис. 26).
 |







Полезно запомнить, что в случаях расположения переменных х и у одновременно внутри знака модуля, графики многозначных функций следует строить, применяя это свойство двойной чётности.
Изобразите в плоскости ХОУ множество всех точек, координаты которых удовлетворяют равенству ││х│ + │у│- 3│=2.
При построении используем двойную чётность и способ разбиения на два уравнения, как и в предыдущем примере. Работая в первом квадранте (при х ≥ 0, у ≥ 0), получим два уравнения у = — х + 5 и у = — х + 1. Выполним построение частей этих прямых, далее отражаем построенные два отрезка симметрично относительно обеих осей координат. Искомым геометрическим местом точек является совокупность двух квадратов, показанных на рис. 27.





№6. Задания для самостоятельного решения
Постройте графики функций:
32) у = — 2 — │х -1│; 33) у = 1/3 │х│ -2; 34) у = │2│х│- 3│;
35) у = — │х-1│; 36) у = 1 — │х│; 37) у = │х + 2│- 1; 38) у = │││х│- 2│ — 1│
39) у = │2х — 1│-│2х +2│; 40) у = │0,5х +1│-│0,5х -2│.
Постройте геометрическое место точек, удовлетворяющих уравнениям:
41) │у│ = 1 – х; 42) │у — 1│ = х; 43) ││х│-│у│ + 3│ = 2; 44) ││х│+
+│у │- 2│ +2; 45) │у + 2│ = │х — 1│.
§5. Построение графиков функций, содержащих знаки модуля, на основе дробно-линейной функции.
Определение. Дробно-линейной (или гиперболической) называют функцию вида
у = 
Эту функцию можно представить также в эквивалентном виде
у = p + 
Чтобы выделить целую часть из дроби, можно разделить «уголком» числитель на знаменатель; тогда получим целое число p, а остаток от деления – k запишем числителем дробной части (знаменатель сохранится).
Чаще в конкретных заданиях применяют другой (искусственный) способ выделения целой части из дроби. Позднее рассмотрим этот способ на примере.
Отметим некоторые особенности графиков гиперболической функции.
1. Функции имеют вертикальную асимптоту х = — d/с.
2. Функции имеют горизонтальную асимптоту у = а/с или у = p.
4. При k/с>0 график расположен к «северо-востоку и к юго-западу» от точки симметрии.



ось О1 У1 : х = — d/с – вертикальная
Рассмотрим пример: построить график дробно-линейной функции
у = 
Выделим целую часть из данной дроби:
у = 


Для построения графика данной функции преобразуем прямоугольную систему координат ХОУ, осуществив параллельный перенос на вектор ОО1= (-1;1), и в преобразованной системе координат Х1О1У1 построим график прямой пропорциональности у = — 4/х (рис. 29).
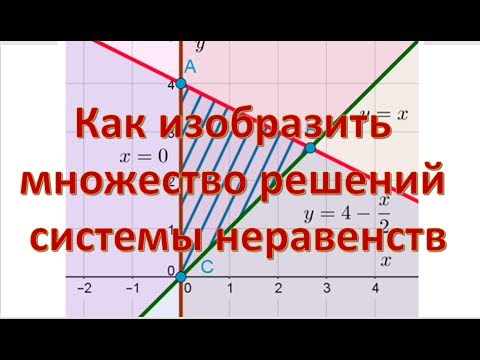
Видео:Как изобразить множество решений системы неравенствСкачать
Найти множество точек координатной плоскости удовлетворяющих уравнению x ^ 2 + y ^ 2 — 6x + 2y = 6?
Математика | 10 — 11 классы
Найти множество точек координатной плоскости удовлетворяющих уравнению x ^ 2 + y ^ 2 — 6x + 2y = 6.
Выделим полные квадраты, используя формулы сокращенного умножения (a + b)² = a² + 2ab + b² и(a — b)² = a² — 2ab + b² :
х² + у² — 6х + 2у = 6
(х² — 2· х· 3 + 3²) — 3² + (у² + 2· у· 1 + 1²) — 1² = 6
(х — 3)² + (у + 1)² — 9 — 1 = 6
(х — 3)² + (у + 1)² = 16 — окружность с центром в точке (3 ; — 1) и радиусом 4
Формула окружности (х — а)² + (у — b)² = R².
Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Решите пожалуйста подробно?
Решите пожалуйста подробно.
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию (x ^ 2 + Y ^ 2 + 2x + 2y) * (4 — x ^ 2 — y ^ 2) знак больше или = 0.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Постройте множество на координатной плоскости, задаваемое неравенством|x| + 3|y|< ; 6?
Постройте множество на координатной плоскости, задаваемое неравенством
Сколько точек с целочисленными координатами принадлежат этому множеству?
Видео:Решение системы неравенствСкачать

Построить на плоскости множество точек, координаты которых удовлетворяют равенству 4у2 — 2х2 — 1 = |4х2 — 2у2 — 1|?
Построить на плоскости множество точек, координаты которых удовлетворяют равенству 4у2 — 2х2 — 1 = |4х2 — 2у2 — 1|.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Найти множество точек координатной плоскости, удовлетворяющих уравнению : 1) х + у — 3 = 0 2)( х — 3) ^ 2 + (y + 2) ^ 2 = 16?
Найти множество точек координатной плоскости, удовлетворяющих уравнению : 1) х + у — 3 = 0 2)( х — 3) ^ 2 + (y + 2) ^ 2 = 16.
Видео:Составляем уравнение прямой по точкамСкачать

Изобразите на координатной прямой множество точек, координаты которых удовлетворяют двойному неравенству ; б) — 15< ; х< ; 27?
Изобразите на координатной прямой множество точек, координаты которых удовлетворяют двойному неравенству ; б) — 15< ; х< ; 27.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Нарисовать любой рисунок координатной плоскости из 20 точек на координатной плоскости?
Нарисовать любой рисунок координатной плоскости из 20 точек на координатной плоскости.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

На координатной плоскости покажите штриховкой множество точек, заданных системной неравенств : ( » ^ » — в квадрате) y≥x ^ 2 y — 4≤0?
На координатной плоскости покажите штриховкой множество точек, заданных системной неравенств : ( » ^ » — в квадрате) y≥x ^ 2 y — 4≤0.
Видео:Уравнение окружности (1)Скачать

СРОЧНО?
Изобразите на координатной плоскости множество точек, удовлетворяющих условиям : у = — х и — 5 ≤ х ≤ 5.
Видео:Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

2. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию : а) х = — 2 ; б) у = 4?
2. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию : а) х = — 2 ; б) у = 4.
3. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию : а) у ≤ 1 ; б) — 3 ≤ х ≤ 1.
4. Изобразите на координатной прямой множество точек, удовлетворяющих условиям : у = — х и — 5 ≤ х ≤ 5.
С. 151) изображен график изменения температуры воздуха в течение одного дня.
Используя график ответьте на вопросы : а) Какова была минимальная температура в этот день?
Б) В какое время суток температура в этот день была равна 2 оС?
В) Когда в течение дня температура повышалась?
6. Запишите предложение на алгебраическом языке : «Расстояние между точками с и — 3 больше или равно 7».
7. Изобразите на координатной плоскости множество точек, удовлетворяющих условиям : у = х 2 и |х| ≤ 4.
8. Прямоугольник задан неравенствами — 1 ≤ х ≤ 4 и 1 ≤ у ≤ 3.
Задайте неравенствами другой прямоугольник, симметричный данному относительно оси абсцисс.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

На координатной плоскости закрасьте множество точек (х, у)?
На координатной плоскости закрасьте множество точек (х, у).
Вопрос Найти множество точек координатной плоскости удовлетворяющих уравнению x ^ 2 + y ^ 2 — 6x + 2y = 6?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
5 + х = 5 х = 5 — 5 х = 0. У + 15 = 15 у = 15 — 15 у = 0. Х — 4 = 0 х = — 4. 28 — а = 28 а = 28 + 28 а = 56.
А) x = 5 — 5 = 0 b)y = 15 — 15 = 0 c)x = 0 + 4 = 4 d)a = 28 — 28 = 0.
А) 280, 70, 350, 20 б) 4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г) 5000000, 32000000.
А)280, 70, 350, 20 б)4600, 14000, 800, 3200 в) 3000, 9000, 26000, 25000 г)5000000, 32000000.
Представим, что x — это сколько страниц занимает расскуз, тогда x×3 — это сколько страниц занимает повесть x + (x×3) = 68 x + 3x = 68 4x = 68 x = 68 : 4 x = 17 — рассказ 17×3 = 51 — повесть.
Т. к. Собрали всего 61 орех, а вова собрал четное число, то остальные дети в сумме собрали нечетное количество( т. К. 61 — четное число = нечетное) и т. К. они собирали только нечетное количество значит детей было нечетное число( т. К. нечетное п..
1) 33 : 3 = 11 (кусков) картона разрезали 2) 17 — 11 = 6 (кусков) картона Ответ : 6 кусков картона осталось неразрезанными.
1)1000 : 100 = 10 2)904 3)450 : 10 = 45 4)1000 : 10 = 100 5)200 — 100 = 100.
1) 7(х + у) / 21 = х + у / 3 2)4(2m — n) / 4m = 2m — n / m 3)3(3a + 4b) / 3 = 3a + 4b 4)9(5c + 2d) / 27d = 5c + 2d / 3d 5)x(5 — y) / x = 5 — y 6)2m(3n — 2) / 2m = 3n — 2.
Возможно одинакого. Если Аня поймала 4, а Вера — 1 Боря — 3, Гена — 2.
🌟 Видео
№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Алгебра с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

9 класс - Алгебра - Неравенства с двумя переменными. Изображение на координатной плоскостиСкачать

Неравенства с двумя переменными. 9 класс.Скачать


























































