Постройте линейное уравнение связи между показателями урожайность и уровень механизации работ

МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ

«МИТСО»

Гомельский филиал

Кафедра математики и информационных технологий

ПРАКТИЧЕСКИЕ ЗАДАНИЯ

К зачету по дисциплине

«Эконометрика и экономико-математические методы и модели»

Для студентов заочной формы обучения

Гомель 2014

Индивидуальное практическое задание к зачету состоит из четырех примеров, отражающих содержание следующих тем дисциплины:

пример 1 – «Парная линейная регрессия»;

пример 2 – «Множественная линейная регрессия»;

пример 3 – «Временные ряды»;

пример 4 – «Модель управления товарными запасами».

Вариант индивидуального задания определяется в соответствии с первыми буквами фамилии, имени, отчества студента (например, студент Иванов Александр Петрович выполняет примеры 1.9 и 2.9 (по фамилии), пример 3.1 (по имени) и пример 4.5 (по отчеству)).

Индивидуальное задание, выполненное не по своему варианту, не зачитывается. Номер каждого примера в работе указывается в обязательном порядке. Перед решением каждой задачи обязательно записывается ее условие.

Решения примеров следует излагать подробно и аккуратно, объясняя все действия. При этом решения первых трех примеров должны дополняться соответствующими компьтерными распечатками.

ВАРИАНТЫ ПРАКТИЧЕСКИХ ЗАДАНИЙ

Пример 1

«Парная линейная регрессия»

Задание 1.1.По статистическим данным, представленным в таблице, построить линейную модель зависимости объема выпуска продукции от величины основных фондов . С помощью показателей корреляции и детерминации оценить качество построенной модели и осуществить точечный прогноз при .

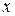
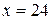
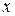Задание 1.2.В таблице приведены данные о среднемесячной начисленной заработной плате 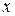и доле денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода.

1) Построить корреляционное поле и визуально оценить форму связи между переменными.

2) Рассчитать параметры уравнения линейной парной регрессии.

3) Оценить тесноту связи с помощью показателей корреляции и детерминации.

4) Оценить с помощью средней ошибки аппроксимации точность модели.

5) Оценить с помощью -критерия Фишера статистическую надежность результатов моделирования.

6) Рассчитать прогнозное значение результата, если среднемесячная начисленная заработная плата равна 320 условных денежных единиц.

Задание 1.3.В таблице приведены статистические данные о среднем размере назначенных пенсий и прожиточном минимуме.

1) Построить корреляционное поле и визуально оценить форму связи между переменными.

2) Рассчитать параметры уравнения линейной парной регрессии.

3) Оценить тесноту связи с помощью показателей корреляции и детерминации.

4) Оценить с помощью средней ошибки аппроксимации точность модели.

5) С помощью -критерий Фишера оценить статистическую надежность результатов моделирования.

6) Рассчитать прогнозное значение результата, если прожиточный минимум составляет 220 условных денежных единиц.

Задание 1.4.В таблице приведены данные об уровне механизации работ 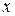и производительности труда для 14 однотипных предприятий.

1) оценить тесноту связи между переменными с помощью линейного коэффициента корреляции;

2) найти параметры уравнения линейной регрессии;

3) найти коэффициент детерминации и пояснить его смысл;

4) проверить значимость уравнения с помощью -критерия;

5) оценить точечный и интервальный прогнозы на предприятиях с уровнем механизации работ 60%.

Задание 1.5. По статистическим данным построить парную линейную модель, отражающую зависимость удельного веса бракованной продукции от доли рабочих со специальной подготовкой. С помощью критерия Стьюдента оценить статистическую значимость коэффициентов уравнения.

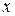
Удельная доля рабочих со специальной подготовкой, %,	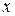Удельный вес бракованной продукции, %,
15,1	18,6
20,2	14,7
30,4	11,3
40,3	9,5
45,4	8,4
55,1	6,3
60,6	5,5
70,8	3,6

Задание 1.6.По статистическим данным, описывающим зависимость уровня рентабельности на предприятии от скорости товарооборота, построить уравнение парной линейной регрессии. Определить общее качество и статистическую значимость уравнения.

Число оборотов,	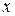Уровень рентабельности, %,
5,49	0,78
4,68	0,38
4,66	0,21
4,53	0,51
4,56	0,95
6,02	1,05
5,72	0,83
5,43	0,99

Задание 1.7.Имеются данные о расходах на питание и душевом доходе для девяти групп семей.

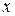
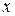1) построить корреляционное поле и визуально оценить форму связи между переменными;

2) построить уравнение парной линейной регрессии;

3) оценить значимость коэффициентов полученной модели;

4) оценить общее качество модели;

5) осуществить точечный прогноз при .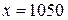

Задание 1.8.Имеются данные по 18 сельскохозяйственным предприятиям.

1) найти коэффициент корреляции между урожайностью зерновых культур и качеством земли;

2) построить уравнение линейной регрессии, которое характеризует зависимость между качеством земли и урожайностью;

3) оценить качество построенной модели;

4) осуществить точечный прогноз урожайности зерновых культур, если качество земли 48 баллов.

Задание 1.9.По данным, представленным в таблице, построить линейное уравнение регрессии, отражающее зависимость стоимости квартиры от ее жилой площади.

Для построенного уравнения вычислить:

1) коэффициент линейной корреляции,

2) коэффициент детерминации;

3) коэффициент аппроксимации.

Осуществить точечный прогноз по построенной модели в случае, когда площадь квартиры составляет 41 кв. м.

Задание 1.10.На основе статистических данных, приведенных в таблице, необходимо:

1) построить уравнение линейной парной регрессии между общей площадью квартиры 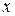и ее ценой ;

2) вычислить линейный коэффициент корреляции и коэффициент детерминации (сделать выводы);

3) вычислить коэффициенты регрессии и оценить их статистическую значимость;

4) изложить экономическую интерпретацию коэффициентов регрессии;

5) осуществить точечный прогноз цены квартиры, если ее площадь составляет 65 квадратных метров.

Видео:Множественная регрессияСкачать

Методические указания для студентов по проведению практических занятий по дисциплине «Статистика» (стр. 11 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

1) составить уравнение множественной зависимости производительности труда, обосновав систему факторов, включенных в модель;

2) определить совокупный коэффициент корреляции и частные коэффициенты корреляции;

3) сопоставить роль различных факторов в формировании моделируемого показателя.

Результативный показатель – годовая производительность труда работника y.

Вооруженность труда основным капиталом – x1;

Удельный вес оборудования в стоимости основного капитала – x2;

Текучесть кадров – x3;

Интегральный показатель использования рабочего времени – x4.

Для определения возможности включения факторов в модель строится матрица парных коэффициентов корреляции (с использованием ЭВМ). Результаты расчета дали следующую матрицу:

Цифры первой строки матрицы парных коэффициентов корреляции показывает, что фактор x3 (текучесть кадров) не следует включать в модель, так как связь результативного показателя с ним слабая (rx3y =0,249). С остальными факторами связь тесная, и, если нет мультиколлинеарности, они могут быть включены в модель.

Сначала проверяется возможность включения в модель факторов x1 и x2. В качестве критерия принимается соблюдение следующих неравенств:

Фактически эти неравенства не соблюдаются, так как

Фактически эти неравенства соблюдаются так как

Таким образом, в модель множественной зависимости могут быть включены два фактора: Х1 и Х4. Линейное уравнение имеет следующий вид:

Ŷ = a + b1x1 + b4x4

Система нормальных уравнений для нахождения параметров a, b1 и b4 следующая:

Σy = na + b1Σx1 + b4Σx4

Σyx1 = aΣx1 + b1 + b4Σx4 · x1

Σyx4 = aΣx4 + b1Σx1 · x4 + b4Σ

3960 = 12a + b1*165,6 + b4*10,44

54937,8 = a*165,6 + b1*2303 + b4*144,85

3459,9 = a*10,44 + b1*144,85 + b4*9,127

Решение системы уравнений дает следующие значения параметров:

a = 48,27; b1 = 4,43; b4 = 253,63.

Модель зависимости производительности труда от факторов имеет следующий вид:

ŷ = 48,27 + 4,43×1 + 253,63×4

Значения результативного признака, рассчитанные по уравнению связи, представлены в таблице:

Вспомогательная таблица для расчета ошибки модели

Годовая произ-ть труда работника (тыс. руб.), y

Теоретический уровень годовой произ-ти труда работника по уравнению связи (тыс. руб.), ŷ

По данным этой же таблицы исчисляется средняя квадратическая ошибка уравнения:

Se =

Следовательно, уравнение хорошо отображает взаимосвязь производительности труда и двух ее факторов.

Определяется совокупный коэффициент корреляции по следующей формуле:

R=

R=

(парные коэффициенты корреляции взяты из матрицы).

Близость совокупного коэффициента корреляции к единице означает: роль не учтенных в модели факторов ничтожна, и есть основания считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов.

Частные коэффициенты корреляции следующие:

а) частный коэффициент корреляции между результативным признаком y и фактором x1 при элимировании фактора Х4:

=0,967;

б) частный коэффициент корреляции между результативным признаком y и фактором Х4 при элимировании фактора Х1:

Сопоставление полученных частных коэффициентов корреляции с вычисленными ранее парными коэффициентами корреляции подтверждает наличие тесной связи между результативным и факторными признаками.

Для сравнения роли отдельных факторов в формировании показателя производительности труда определяются коэффициенты эластичности.

а) для фактора

б) для фактора

Следовательно, при увеличении вооруженности труда основным капиталом на 1% производительность труда возрастает лишь на 0,185%. Увеличение показателя использования рабочего времени на 1% повлечет рост производительности труда на 0,669%.

3 По группе однородных предприятий имеются данные об объеме выпущенной продукции и уровне механизации трудоемких и тяжелых работ:

Уровень механизации трудоемких и тяжелых работ, %

Видео:Множественная регрессия в ExcelСкачать

ПРАКТИЧЕСКАЯ ЧАСТЬ

12.15 Имеются следующие данные об уровне механизации работ Х(%) и производительности труда Y (т/ч) для 14 однотипных предприятий.

Необходимо оценить тесноту и направление связи между переменными с помощью коэффициента корреляции; проверить значимость коэффициента корреляции и построить для него 95%-ный доверительный интервал.

Для нахождения коэффициента корреляции используем формулу 1.35′. Находим все необходимые суммы: После подстановки всех значений получаем r=0,969, что говорит о достаточно тесной связи между величинами Значимость коэффициента корреляции В данной задаче , что говорит о большой значимости Построение доверительного интервала По формуле 1.48 строим доверительный интервал 12.16. При исследовании корреляционной зависимости по данным 20 предприятий между капиталовложениями Х (млн. руб.) и выпуском продукции Y (млн. руб.) получены следующие уравнения регрессии: и . Найти: а) коэффициент корреляции между рассматриваемыми признаками и оценить его значимость на 5%-ом уровне; б) средние значения капиталовложений и выпуска продукции. Согласуется ли полученный в п. а) результат с утверждением о том, что генеральный коэффициент корреляции между Х и Y равен 0,95? а) Коэффициент корреляции между рассматриваемыми признаками определим по формуле Согласно полученным уравнениям регрессии Коэффициент корреляции равен Оценим его значимость на 5%-ом уровне: Гипотеза отвергается, то есть выборочный коэффициент корреляции значимо отличается от нуля, если Табличное значение . Поскольку наблюдаемое значение статистики превышает критическое, то гипотеза отвергается, следовательно, выборочный коэффициент корреляции значим. б) Средние значения капиталовложений и выпуска продукции являются совместным решением системы из двух уравнений регрессий: Среднее значение капиталовложений , среднее значение выпуска продукции . Проверим, согласуется ли полученный в п. а) результат с утверждением о том, что генеральный коэффициент корреляции между Х и Y равен 0,95. Так как коэффициент корреляции X и Y значим), то построим доверительный интервал для генерального коэффициента корреляции с, применяя z-преобразование Фишера: При уровне значимости квантиль нормального распределения . Определим доверительные границы для величины : Производим обратный пересчет в Итак, с вероятностью 0,95 можно утверждать, что коэффициент корреляции генеральной совокупности содержится в интервале: Как видим, значение генерального коэффициента корреляции между Х и Y, равное 0,95, попадает в полученный интервал. Следовательно, полученный в п. а) результат согласуется с утверждением о том, что генеральный коэффициент корреляции между Х и Y равен 0,95. 12.17. При исследовании корреляционной зависимости между ценой на нефть Х и индексом нефтяных компаний Y получены следующие данные: (ден. ед.), (усл. ед.), , , . Необходимо: а) составить уравнения регрессии Y по Х и Х по Y; б) используя соответствующее уравнение регрессии, найти среднюю величину индекса при цене на нефть 16,5 ден. ед. а) Составим уравнения регрессии Y по Х и Х по Y: б) Используя уравнение регрессии Y по Х, найдем среднюю величину индекса при цене на нефть 16,5 ден. ед.: 12.18. При исследовании корреляционной зависимости между объемом продукции Х (единиц) и ее себестоимости Y (тыс. руб.) получено следующее уравнение регрессии Y по Х: . Составить уравнение регрессии Х по Y, если коэффициент корреляции между этими признаками оказался равным -0,8, а средний объем продукции единиц. Уравнения регрессий имеют вид Уравнение регрессии Х по Y имеет вид 12.19. С целью исследования влияния факторов Х1 — среднемесячного количества профилактических наладок автоматической линии и Х2 — среднемесячного числа обрывов нити на показатель Y — среднемесячную характеристику качества ткани (в баллах) по данным 37 предприятий легкой промышленности были вычислены парные коэффициенты корреляции: , и . Определить: а) частные коэффициенты корреляции и и оценить их значимость на 5%-ом уровне; б) множественный коэффициент корреляции и оценить его значимость на уровне ; в) множественный коэффициент детерминации. Пояснить смысл полученных коэффициентов. а) По формуле вычислим частные коэффициенты корреляции и : Оценим значимость полученных коэффициентов. Полагаем условно . По формуле находим статистики коэффициентов: По таблице -распределения Стьюдента находим . Так как и , то частные коэффициенты корреляции и значимы. Сравнивая частные коэффициенты корреляции и с соответствующими парными коэффициентами и , видим, что за счет «очищения связи» наибольшему изменению подвергся коэффициент корреляции между Х2 — среднемесячным числом обрывов нити и Y — среднемесячной характеристикой качества ткани (в баллах) (изменилась не только его величина, но даже и знак: ; , причем оба эти коэффициента значимы). Итак, между Х2 — среднемесячным числом обрывов нити и Y — среднемесячной характеристикой качества ткани (в баллах) существует слабая прямая корреляционная связь (). Если же устранить (элиминировать) влияние переменной Х1 — среднемесячного количества профилактических наладок автоматической линии, то в чистом виде Y — среднемесячная характеристика качества ткани (в баллах) находится в обратной по направлению (но сильной по тесноте) связи с Х2 — среднемесячным числом обрывов нити (). Аналогично, между Х1 — среднемесячным количеством профилактических наладок автоматической линии и Y — среднемесячной характеристикой качества ткани (в баллах) существует слабая прямая корреляционная связь (). Если же устранить влияние переменной Х2 — среднемесячного числа обрывов нити, то в чистом виде Y — среднемесячная характеристика качества ткани (в баллах) находится в прямой по направлению (и сильной по тесноте) связи с Х1 — среднемесячным количеством профилактических наладок автоматической линии (). б) Вычислим множественный коэффициент корреляции : Между Y — среднемесячной характеристикой качества ткани (в баллах), с одной стороны, и Х1 — среднемесячным количеством профилактических наладок автоматической линии и Х2 — среднемесячным числом обрывов нити, с другой стороны, существует очень тесная взаимосвязь. Для оценки значимости вычислим и по таблицам -распределения найдем . Так как , то значимо отличается от нуля. в) Множественный коэффициент детерминации показывает, что вариация Y — среднемесячной характеристикой качества ткани (в баллах) на 82,3% объясняется вариацией Х1 — среднемесячного количества профилактических наладок автоматической линии и Х2 — среднемесячного числа обрывов нити. 12.20. При приеме на работу семи кандидатам на вакантные должности было предложено два теста. Результаты тестирования (в баллах) приведены в таблице: 🎦 Видео Парная регрессия: линейная зависимостьСкачать Коэффициент детерминации. Основы эконометрикиСкачать Эконометрика Линейная регрессия и корреляцияСкачать Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать Что такое линейный и логарифмический переменный резистор.Чем они отличаются и где применяются.Скачать Эконометрика. Линейная парная регрессияСкачать Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать Линейная регрессияСкачать Эконометрика. Нелинейная регрессия. Степенная функция.Скачать Как применять линейную регрессию?Скачать Множественная степенная регрессияСкачать Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать 5 задач по эконометрикеСкачать Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства