Построить уравнение регрессии со статистически значимыми факторами

Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
,
где — оценка параметра регрессии, полученная по наблюдаемым данным;
μ_a – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
, где r_yx — оценка коэффициента корреляции, полученная по наблюдаемым данным; m_r – стандартная ошибка коэффициента корреляции r_yx.
Для линейного парного уравнения регрессии:
.
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t _{( b =0)} = t _(r=0).

Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
69	124	4761	15376	8556	128.48	491.36	20.11	367.36
83	133	6889	17689	11039	141.4	173.36	70.56	26.69
92	146	8464	21316	13432	149.7	0.03	13.71	14.69
97	153	9409	23409	14841	154.32	46.69	1.73	78.03
88	138	7744	19044	12144	146.01	66.69	64.21	0.03
93	159	8649	25281	14787	150.63	164.69	70.13	23.36
74	145	5476	21025	10730	133.1	1.36	141.68	200.69
79	152	6241	23104	12008	137.71	34.03	204.21	84.03
105	168	11025	28224	17640	161.7	476.69	39.74	283.36
99	154	9801	23716	15246	156.16	61.36	4.67	117.36
85	127	7225	16129	10795	143.25	367.36	263.91	10.03
94	155	8836	24025	14570	151.55	78.03	11.91	34.03
1058	1754	94520	258338	155788	1754	1961.67	906.57	1239.67

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S _a = 0.2704
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).

Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.812):
(a — t_табл·S _a; a + t_табл·S_a)
(0.4325;1.4126)
(b — t_табл·S _b; b + t_табл·S_b)
(21.3389;108.3164)
2) F-статистики

Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.

Пример №2 . По территориям региона приводятся данные за 199Х г.; <table хСреднедневная заработная плата, руб., у17813328214838713447915458916261061957671398881589731521087162117615912115173 Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
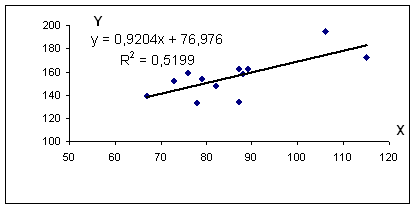
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.

Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели. <table 2y 2x·yy(x)(y i — y ) 2(y-y(x)) 2(x i — x ) 2|y-y x |:y7813360841768910374148,77517,56248,757,510,11868214867242190412136152,4560,0619,8212,840,03018713475691795611658157,05473,06531,482,010,1727915462412371612166149,693,0618,5743,340,0288916279212624414418158,8939,069,6411,670,0192106195112363802520670174,541540,56418,52416,840,1049671394489193219313138,65280,560,1258345,340,00268815877442496413904157,975,060,00075,840,00027315253292310411096144,1714,0661,34158,340,05158716275692624414094157,0539,0624,462,010,03057615957762528112084146,9310,56145,791,840,0759115173132252992919895182,83297,5696,55865,340,0568

102718698990729437716180818693280,251574,922012,920,6902 2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим t_крит:
t_крит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bx_p ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 94

(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (10;0.05) = 1.812

Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-t_a)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Оценить статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента

1) Оценим статистическую значимость уравнения регрессии с помощью критерия Фишера. Расчетное значение F-критерия Фишера можно найти в регрессионном анализе (рисунок 5).

Дисперсионный анализ
df	SS	MS	F	Значимость F
Регрессия	1,32E+12	1,32E+12	2447,317	4,94E-18
Остаток	8,12E+09	5,41E+08
Итого	1,33E+12

Рисунок 5.Фрагмент регрессионного анализа для однофакторной модели

Так как F>F_табл, то уравнение однофакторной регрессии статистически значимо на 95% уровне значимости. Таким образом, связь У с включенным в модель фактором существенна.

2) Коэффициент уравнения регрессии признается значимым, если наблюдаемое значение t-статистики Стьюдента для этого коэффициента больше, чем критическое табличное значение статистики Стьюдента (для заданного уровня значимости).

Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	17243,98	6178,659	2,790894
X2	0,618526	0,012503	49,47036

Рисунок 6.Фрагмент регрессионного анализа для однофакторной модели

Фактические значения t-критериев сравниваются с табличным значением при степенях свободы n-k-1 = 17-1-1=15 и уровне значимости α=0,05.

Фактор Х2 статистически значим (_tнабл > _tтабл).

4. Построить уравнение регрессии со статистически значимыми факторами. Оценить качество уравнения регрессии с помощью коэффициента детерминации R 2 . Оценить точность построенной модели.

Уравнение регрессии: У = 17243,98+0,62Х2

Качество уравнения регрессии оценивается коэффициентом детерминации R 2 .

Регрессионная статистика
Множественный R	0,996949
R-квадрат	0,993908
Нормированный R-квадрат	0,993502
Стандартная ошибка	23264,62
Наблюдения

Рисунок 7. Фрагмент регрессионного анализа для однофакторной модели

Величина R 2 = 0,993908 означает, что фактором У (объем выпуска продукции) можно объяснить 99,3% вариации (разброса) объема выпуска продукции.

Уровень точности модели характеризует степень отклонения в среднем фактических значений результативной переменной У от ее значений, полученных по модели регрессии (предсказанных). Для оценки уровня точности используются различные ошибки: средняя относительная, стандартная и другие.

Cтандартная ошибка модели выводится в первой таблице «Регрессионная статистика» (рис. 8) отчета по регрессионному анализу.

Регрессионная статистика
Множественный R	0,996949
R-квадрат	0,993908
Нормированный R-квадрат	0,993502
Стандартная ошибка	23264,62
Наблюдения

Рисунок 8. Фрагмент регрессионного анализа для однофакторной модели

Точность модели тем лучше, чем меньше ее стандартная ошибка (это же имеет место и при использовании для оценки уровня точности других видов ошибок). Однако, понятие «чем меньше» является относительным и зависит от порядка чисел, представляющих данные задачи. Поэтому модель считается точной, если стандартная ошибка модели меньше стандартной ошибки (среднеквадратического отклонения) результативного признака Y . Стандартную ошибку легко найти в Excel с помощью статистической функции СТАНДОТКЛОН.

В данном случае стандартная ошибка модели равна 23 264,62, а среднеквадратическое отклонение (или стандартная ошибка) фактора Sу =288 607,7

Так как

Уmax(90%) =17243,98+0,62*1974472*0,9 = 1118999,356

Доверительные интервалы для отдельных значений результирующей переменной можно определить, рассчитав вначале для каждого уровня ошибки моделирования по формуле

= 23 264,62

U(0,05) = 23 264,62*2,13 = 49553,64

U(0,1) = 23 264,62*1,75 = 40713,085

Затем определяется сам доверительный интервал:

нижняя граница – ,

верхняя граница – ,

где – i-ый уровень предсказанного значения результата

Объем выпуска продукции при максимальных значениях фактора Х2.

Уmax=	1 241 416,62
U(0,05) =	49553,64
У max-U(0,05)	У max+U(0,05)
1191862,98	1290970,26
У max =	1 241 416,62
U(0,1) =	40713,085
У max-U(0,01)	У max+U(0,01)
1200703,535	1282129,705

Прогноз объема выпуска продукции, если прогнозные значения фактора составляют 75% от их максимальных значений.

Уmax(75%)=	935373,46
U(0,05) =	49553,64
Уmax(75%)-U(0,05)	Уmax(75%)+U(0,05)
885819,82	984927,1
Уmax(75%)=	935373,46
U(0,1) =	40713,085
Уmax(75%)-U(0,1)	Уmax(75%)+U(0,1)
894660,375	976086,545

Прогноз объема выпуска продукции, если прогнозные значения фактора составляют 90% от их максимальных значений.

Пример построения эконометрической модели в EXCEL

По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y, млн.руб.) от величины доходов по кредитам (X1, млн.руб.), доходов по депозитам (X2, млн.руб.) и размера внутрибанковских расходов (X3, млн.руб.).

Y

X1

X2

X3

1. Осуществить выбор факторных признаков для построения многофакторной регрессионной модели.

2. Рассчитать параметры регрессионной модели. Оценить ее качество.

3. Для характеристики модели определить:

4. средние коэффициенты эластичности;

7. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

8. Построить регрессионную модель со статистически значимыми факторами. Оценить ее качество.

9. Определить точечный и интервальный прогноз результативного показателя.

I. Выбор факторных признаков для построения модели осуществляется с помощью матрицы коэффициентов парной корреляции. Для её построения необходимо:

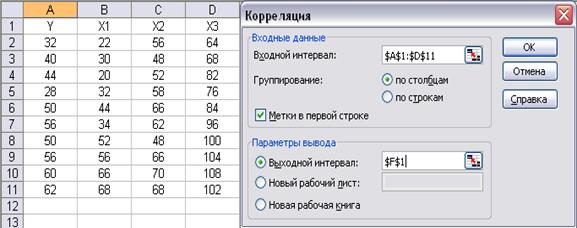
выбрать Сервис->Анализ данных->Корреляция

заполнить необходимые поля диалогового меню (рисунок 1)

Рис.1. Ввод параметров инструмента «Корреляция»

Результаты представлены на рисунке 2.

Рис.2. Таблица коэффициентов парных корреляций

Для выявления явления мультиколлинеарности необходимо проанализировать коэффициенты парной корреляции между факторными признаками. Если имеют место коэффициенты, значение которых по модулю больше 0,8, то, следовательно, мультиколлинеарность присутствует, и это явление необходимо устранять. Если же значения коэффициентов парной корреляции между факторными признаками, взятые по модулю, меньше величины 0,8, то явление мультиколлинеарности отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии.

Так как , т.е. между факторными признаками X1 и X3 существует явление мультиколлинеарности, то для построения модели выбираем тот факторный признак, который оказывает большее влияние на результативный признак (фактор, для которого коэффициент парной корреляции с результативным признаком, взятый по модулю, является большим).

Следовательно, фактор X3 оказывает большее влияние на результативный признак (Y) и этот фактор рекомендуется в модели оставить. Фактор X1 оказывает меньшее влияние на результативный признак (Y) и этот фактор рекомендуется из модели исключить.

Таким образом, для построения модели множественной регрессии выбираются два факторных признака — Х2 (величина доходов по депозитам) и Х3 (величина внутрибанковских расходов).

II. Расчет параметров регрессионной модели можно осуществить с помощью инструмента анализа данных Регрессия, отличие заключается в том, что в качестве диапазона значений фактора X необходимо указать диапазон значений факторов X2 и X3 (рисунок 3).

Рис.3. Ввод параметров регрессии

Результаты построение множественной регрессии представлены на рисунке 4.

Рис.4. Вывод итогов регрессии

На основании полученных данных можно записать уравнение множественной регрессии

Y=-16,2872 + 0,197247*X2 + 0,592429*X3

Оценим качество построенной модели множественной регрессии по следующим направлениям:

Коэффициент детерминации = 0.794176 достаточно близок к 1, следовательно, качество модели можно признать высоким.

Критерий Фишера F = 13,50486 > Fтабл = 4,74 , следовательно, уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования экономических процессов.

Для вычисления Fтабл необходимо определить:

— степень свободы числителя m=2 (число факторных признаков);

— степень свободы знаменателя n-m-1=10-2-1=7;

— уровень значимости =0,05.

III. Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности, b — и D — коэффициентов.

Коэффициент эластичности определяется:

, (1)

где — среднее значение соответствующего факторного признака,

— среднее значение результативного признака.

bi – коэффициенты регрессии соответствующих факторных признаков.

ß-коэффициент определяется по следующей формуле:

, (2)

где — среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),

— СКО результативного признака.

∆-коэффициент определяется по следующей формуле:

, (3)

где — коэффициент парной корреляции результативного и соответствующего факторного признаков,

— коэффициент детерминации.

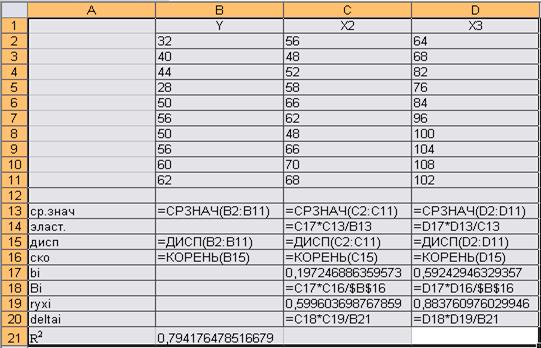
На рисунке 5 представлены формулы расчетов описанных выше коэффициентов

Рис.5. Формулы расчетов коэффициентов

Результаты вычислений представлены в таблице 2.

Результаты расчета бета-, дельта- и коэффициентов эластичности

Y	X2	X3
Ср.знач	47,8	59,4	88,4
Эласт.	0,245	0,881
Дисп	134,6	67,6	247,8
СКО	11,60	8,221	15,74
bi	0,197	0,592
	0,139	0,803
	0,599	0,883
	0,105	0,894

Частный коэффициент эластичности показывает, на сколько процентов изменится среднее значение результативного признака, если среднее значение конкретного факторного признака изменится на 1 %, т.е., при увеличении на 1% величины доходов по депозитным операциям (Х2) прибыль банка увеличится на 0,245 % (Э2 = 0,245), при увеличении на 1% размера внутрибанковских расходов (X3) объём прибыли увеличится на 0,88% (Э3 =0,881).

β-коэффициент показывает, на какую величину изменится СКО результативного признака, если СКО конкретного факторного признака изменится на 1 единицу, т.е. при увеличении на 1 единицу СКО доходов по депозитам (X2), СКО объёма прибыли увеличится на 0,14 ( =0,139774); при увеличении на 1 единицу СКО внутрибанковских расходов СКО прибыли организации увеличится на 0,804 единицы ( = 0,803801 ).

∆-коэффициент показывает удельный вес влияния конкретного факторного признака в совместном влиянии всех факторных признаков на результативный показатель, т.е. удельный вес влияния внутрибанковских расходов (X3) на объём прибыли (результативный признак) составляет 89,4% (∆3 = 0,8944), а удельное влияние доходов по депозитам (Х2) на прибыль составляет 10,5 % ( ∆2 = 0,1055).

IV. Для оценки статистической значимости факторных признаков модели множественной регрессии используется t-критерий Стьюдента.

С помощью функции СТЬЮДРАСПОБР(0,05;7) определим табличное значение t табл = 2,364624.

Сравним расчетные значения t-статистики, взятые по модулю, с табличным значением этого критерия (расчетные значения берутся из столбца t-статистика таблицы 3 регрессионного анализа).

Результаты регрессионного анализа

Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-16,2872	14,93	-1,0904	0,311	-51,60	19,03	-51,60	19,03
X2	0,197	0,295	0,66857	0,525	-0,500	0,894	-0,500	0,894
X3	0,592	0,154	3,84478	0,006	0,228	0,956	0,228	0,956

t х2 = 0,668573 tтаб=2,364624, следовательно, фактор Х3 признается статистически значимым и информативным. Такой фактор рекомендуется в модели регрессии оставить.

Построим регрессионную модель со статистически значимыми факторами. Для конкретного примера статистически значимым фактором является только фактор Х3 (величина внутрибанковских расходов). Подробное построение регрессионных моделей рассмотрено ранее. Осуществим следующие установки в окне Регрессия (рисунок 6).

Рис.6. Диалоговое окно Регрессия

Получим следующие результаты (рисунок 7)

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,88376
R-квадрат	0,78103
Нормированный R-квадрат	0,75366
Стандартная ошибка	5,75868
Наблюдения
Дисперсионный анализ
df	SS	MS	F	Знач. F
Регрессия	946,300	946,300	28,53	0,000693
Остаток	265,299	33,1624
Итого	1211,6
Коэфф.	Стандар ошибка	t-статист.	P-Знач.	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-9,78049	10,93189	-0,894	0,397	-34,9895	15,42	-34,9895	15,4285
X3	0,65136	0,12193	5,34184	0,000693	0,370178	0,9325	0,370178	0,932548

Рис.7. Вывод итогов регрессии

Запишем уравнение зависимости прибыли организации от величины внутрибанковских расходов (Х3):

Y = 0,651363*Х3 – 9,78049

Качество этой модели может быть оценено по коэффициенту детерминации =0,781, следовательно, размер прибыли кредитных организаций на 78,1 % зависит от величины внутрибанковских расходов.

При сравнении качества регрессии y = f (X3) с качеством регрессии
y = f (X2, X3) , имеющей =0,794, можно утверждать, что улучшение качества модели не произошло.

Значение F-критерия Фишера составляет 28,53 > Fтабл (1,8)=5,32 , следовательно, построенное уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования процессов.

Построение точечного прогноза прибыли кредитного учреждения (результативного показателя) может быть осуществлено по уравнению множественной регрессии, построенной в пункте 4 задачи, или по уравнению регрессии, содержащего только статистически значимые факторы (пункт 5 задачи).

Воспользуемся уравнением множественной регрессии, так как качество этой модели признано лучшим:

Для построения точечного прогноза результативного признака необходимо рассчитать точечные прогнозы факторных признаков (величины доходов организации по депозитам и величины внутрибанковских расходов). Для этого построим графики X2(t), X3(t) и тренд по каждому из факторов (рисунок 8, 9).

Рис. 8. Выбор типа диаграммы

Рис.9. Выбор источника данных

На полученной диаграмме необходимо добавить линию тренда:

Диаграмма->Добавить линию тренда.

В настройках тренда в закладке Параметры указать (рисунок 10):

Прогноз вперед на 1 единицу

Показать уравнение на диаграмме

Поместить на диаграмму величину достоверности аппроксимации.

Рис.10. Параметры линии тренда

Результат построения представлен на рисунке 11.

Рис.11. Построение прогноза величины доходов по депозитам (X2)

В полученное уравнение тренда

Х2 = 1,8061*х + 49,467 ,

в котором в качестве факторного признака выступает «время», необходимо подставить следующий момент времени. Так как временной ряд факторного признака Х2 представлен 10 наблюдениями, то следующий момент времени будет представлен числом 11.

X2Прогн.=1,8061*11+49,467 = 69,3341 (млн.руб.)

Осуществляя аналогичные установки для фактора Х3, построим прогноз по величине внутрибанковских расходов (рисунок 12) .

Рис.12. Построение прогноза величины внутрибанковских расходов (X3)

Определим прогнозное значение внутрибанковских расходов из построенного уравнения тренда:

X3Прогн.=4,9455 *11+61,2=115,6005 (млн.руб.)

Рассчитанные значения прогнозов по факторам Х2 и Х3 подставим в уравнение множественной регрессии:

Y=0,197247*X2 + 0,592429*X3 — 16,2872

YПрогн. = 0,197247*X2 Прогн. + 0,592429*X3 прогн. — 16,2872

Определим интервальный прогноз результирующего показателя, для этого рассчитаем ширину доверительного интервала по формуле:

(4)

где = 5,968678 (стандартная ошибка из таблицы регрессионной статистики, рисунок 17),

Y Прогн. – рассчитанное выше значение точечного прогноза результативного признака,

Кр= tтаб= 2,364624 табличный коэффициент Стьюдента, можно определить с помощью функции СТЬЮДРАСПОБР(0,05;7)

— среднее значение результативного признака (прибыли кредитной организации).

Подставляя эти значения в выше записанную формулу, получим:

U(k)= 5,968678*2,364624*√(1+0,1+326,6634/1211,6)= 16,51731

Таким образом, прогнозное значение прибыли кредитных организаций
Yпрогн= 65,873832 , будет находиться между верхней границей, равной
65,873832 + 16,51731 = 82,39113827 (млн.руб.)

и нижней границей, равной

65,873832 – 16,51731= 49,3565254 (млн.руб.)

Вывод: Прогнозное значение прибыли исследуемых кредитных организаций, рассчитанное по уравнению множественной регрессии, будет находиться в интервале от 49,36 мл.руб. до 82,39 млн.руб.

Данное уравнение регрессии признано статистически значимым по критерию Фишера и обладает достаточно высоким качеством, следовательно, результаты расчетов можно признать надежными и достоверными.

💡 Видео