Построить параболу y2 6x найти координаты фокуса и уравнение директрисы (5 видео)

Задача 31453 Пожалуйста помогите 1)определить.

Содержание

Условие
Решение
Построить параболу y2 6x найти координаты фокуса и уравнение директрисы
Как написать хороший ответ?
Примеры решений: кривые второго порядка
Кривые 2-го порядка: решения онлайн
Парабола
Парабола, её форма, фокус и директриса.
Свойства параболы.
Уравнение касательной к параболе.
🎦 Видео

Условие

Пожалуйста помогите
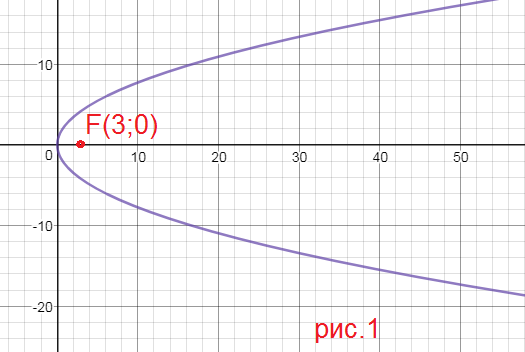
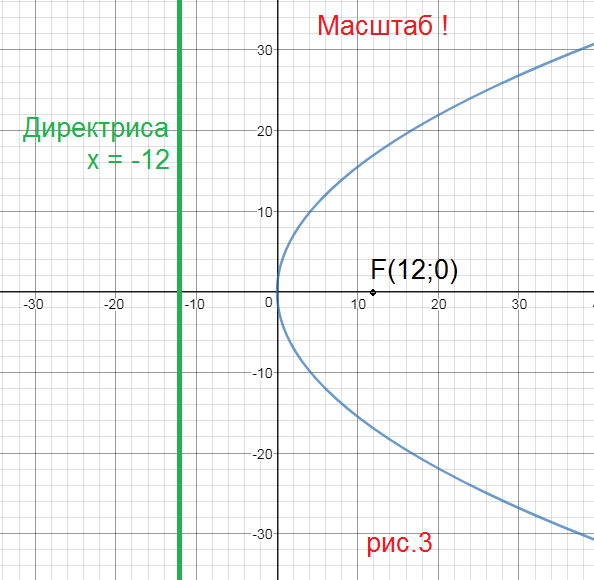
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y

2)найти фокус и уравнение директрисы параболы y^2=24x

Решение

Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2

x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2

y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2

y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2

[b]Решение[/b]:
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох

x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу

2)
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох

Фокус F(12;0)
Уравнение директрисы:
x=-12

см. рис.3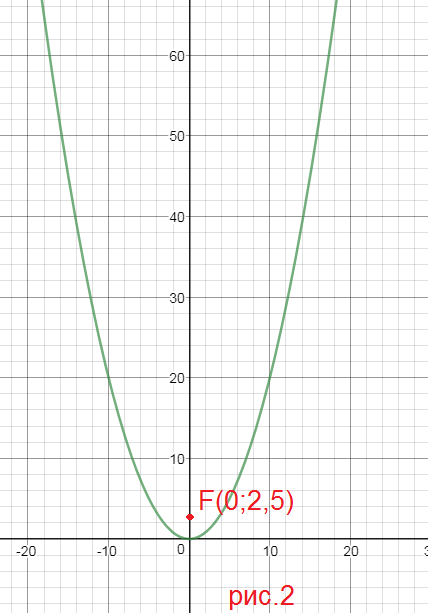

Видео:213. Фокус и директриса параболы.Скачать

Построить параболу y2 6x найти координаты фокуса и уравнение директрисы

Вопрос по алгебре:

Построить параболу y^2=6x. Найти:
1) координаты фокуса
2) уравнение директрисы

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Построение параболы по ее директрисе и фокусуСкачать

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Видео:Как легко составить уравнение параболы из графикаСкачать

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Парабола

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^=2pxlabel
$$
при условии (p > 0).

Из уравнения eqref вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

Рис. 8.11. Парабола.

Видео:Видеоурок "Парабола"Скачать

Свойства параболы.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac

.label
$$

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^=(x-p/2)^+y^) и подставим сюда (y^) из канонического уравнения параболы. Мы получаем
$$
r^=left(x-frac

right)^+2px=left(x+frac

right)^.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac

.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt<left(x-frac

right)^+y^>=x+frac

.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_(x_, y_)), лежащей на ней. Пусть (y_ neq 0). Через точку (M_) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt) или же (y=-sqrt), смотря по знаку (y_).) Для функции (f(x)) выполнено тождество ((f(x))^=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_) и (f(x_)=y_), находим (f'(x_)=p/y_) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_=frac

<y_>(x-x_).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_^=2px_). Теперь уравнение касательной принимает окончательный вид
$$
yy_=p(x+x_).label
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_ neq 0), уравнение eqref превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref справедливо для любой точки на параболе.

Касательная к параболе в точке (M_) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке (M_(x_, y_)). Из уравнения eqref получаем ее направляющий вектор (boldsymbol(y_, p)). Значит, ((boldsymbol, boldsymbol_)=y_) и (cos varphi_=y_/boldsymbol). Вектор (overrightarrow<FM_>) имеет компоненты (x_=p/2) и (y_), а потому
$$
(overrightarrow<FM_>, boldsymbol)=x_y_-frac

y_+py_=y_(x_+frac

).nonumber
$$
Но (|overrightarrow<FM_>|=x_+p/2). Следовательно, (cos varphi_=y_/|boldsymbol|). Утверждение доказано.

Заметим, что (|FN|=|FM_|) (см. рис. 8.12).