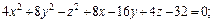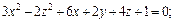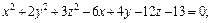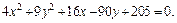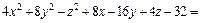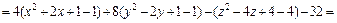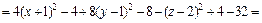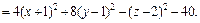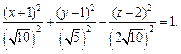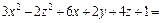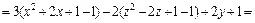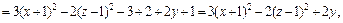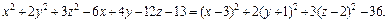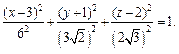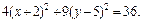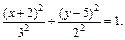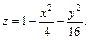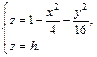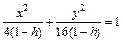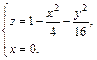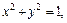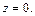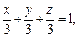8.4. Построение поверхностей
Мы приступаем к изучению формы поверхностей второго порядка, определённых в предыдущем разделе своими каноническими уравнениями. Напомним, что это вторая из двух основных задач аналитической геометрии: зная уравнение поверхности, изучить её геометрические свойства.
Метод, который мы будем применять, называется методом сечений: пересекая поверхность плоскостями, параллельными координатным плоскостям, будем рассматривать линии пересечения и по их виду делать выводы о форме поверхности.
Каноническое уравнение эллипсоида:
Отметим симметрию поверхности: если точка (x, у, z) лежит на эллипсоиде, то и все точки (±x, ±у, ±z) тоже лежат на эллипсоиде. Значит, поверхность симметрична относительно любой из координатных плоскостей. Пересечём эллипсоид плоскостью z = h. Получим линию
Это эллипс, полуоси которого убывают с увеличением |h|. При h = c эллипс превращается в точку, при h > c плоскость z = h не пересекает эллипсоид. Эллипсы получаются и при сечении эллипсоида плоскостями x = h, у = h. Используя эти данные, изображаем поверхность. Числа a, b, c называются полуосями эллипсоида. Если две полуоси равны, то получается эллипсоид вращения. Например, эллипсоид, образованный при вращении эллипса (лежит в плоскости XOZ) вокруг оси OZ. Если a = b = c, то эллипсоид превращается в сферу.
- Поверхности второго порядка: их виды, уравнения, примеры
- Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
- Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
- Эллипсоид
- Мнимый эллипсоид
- Мнимый конус
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Конус
- Эллиптический параболоид
- Гиперболический параболоид
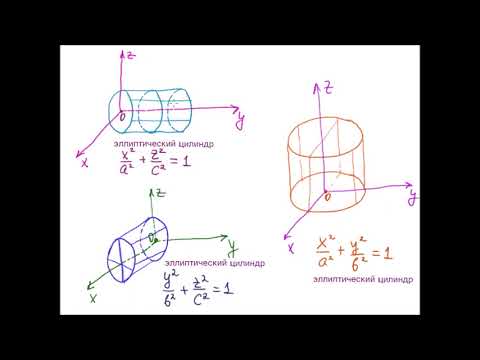
- Эллиптический цилиндр
- Мнимый эллиптический цилиндр
- Мнимые пересекающиеся плоскости
- Гиперболический цилиндр
- Пересекающиеся плоскости
- Параболический цилиндр
- Параллельные плоскости
- Мнимые параллельные плоскости
- Совпадающие плоскости
- Решение примеров на определение вида поверхности второго порядка
- Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
- Поверхности второго порядка
- 📸 Видео
Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядка: их виды, уравнения, примеры
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Видео:Поверхности второго порядкаСкачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут



Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:




Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:




Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:




то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая


получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем 



получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:


Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:


Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

перепишем его в виде

Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

перепишем его в виде

Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :

I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:






Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :


Следовательно, общее уравнение определяет эллиптический параболоид.

I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:





Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением



I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.


Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Поверхности второго порядка
Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:
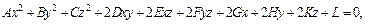
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.
1. Эллипсоид: 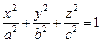
2. Конус второго порядка: 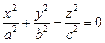
3. Гиперболоиды
1) однополостный: 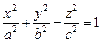 (рис. 15.3); (рис. 15.3); | 2) двуполостный: 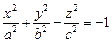 (рис. 15.4). (рис. 15.4). |
Рис. 15.3 Рис. 15.4
4. Параболоиды
1) эллиптический: 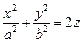 (рис. 15.5); (рис. 15.5); | 2) гиперболический: 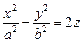 (рис.15.6). (рис.15.6). |
 |  |
Рис. 15.5 Рис. 15.6
5. Цилиндры
1) эллиптический: 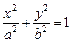 (рис. 15.7); (рис. 15.7); | 2) гиперболический: 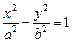 (рис. 15.8); (рис. 15.8); |
 |  |
Рис. 15.7 Рис. 15.8
3) параболический: 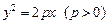
Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в общем уравнении поверхности коэффициенты 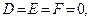
В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

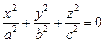
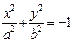
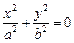
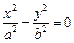
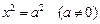
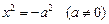

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:
1)
2)
3)
4)
Решение. 1) Воспользуемся методом выделения полных квадратов.
Преобразуем левую часть уравнения:
Значит, заданное уравнение равносильно уравнению
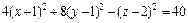
Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).
2) Поскольку
то заданное уравнение равносильно уравнению
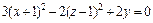
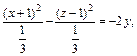
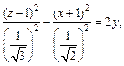
3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:
Поэтому заданное уравнение принимает вид:
или (после деления на 36)
Это уравнение эллипсоида с центром в точке (3, – 1, 2).
4. Методом выделения полных квадратов уравнение 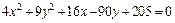
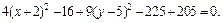
Почленное деление на 36 дает:
Это уравнение эллиптического цилиндра, смещенного в точку
(–2, 5, 0).
Пример 2. Исследовать поверхность методом сечений и построить ее:
Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.
Определим сечение поверхности плоскостями 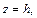
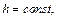
Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением
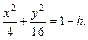
Уравнение (15.23) при 
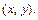
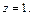
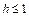
с полуосями 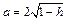
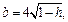
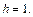
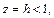
Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:
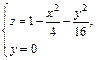
В первом случае имеем кривую 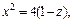
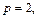
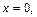
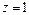
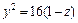
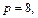
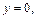
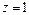
Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид 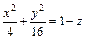
Пример 3. Построить тело, ограниченное поверхностями
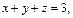
Решение. Уравнение 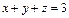
т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.
Уравнение 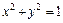
Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.
📸 Видео
Поверхности 2 порядкаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

Как строить сеченияСкачать

Цилиндрические поверхностиСкачать
Практическое занятие: поверхности второго порядкаСкачать

Сечения многогранников. Метод следов.Скачать
Поверхности второго порядка. Поверхности вращенияСкачать
§64 Поверхности вращенияСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Семинар Аналитическая геометрия. Кривые и поверхности второго порядка.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать