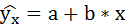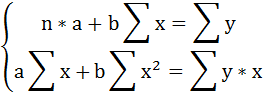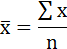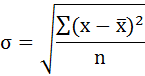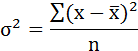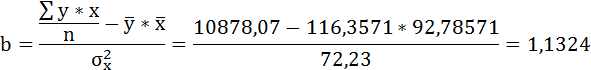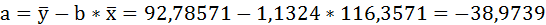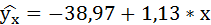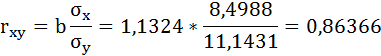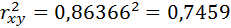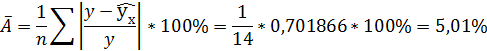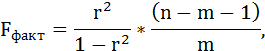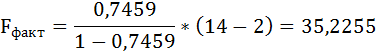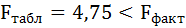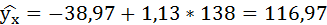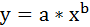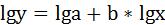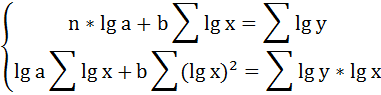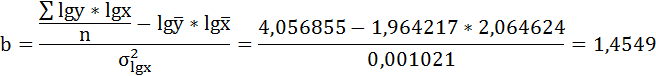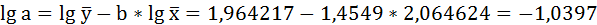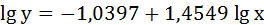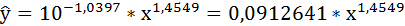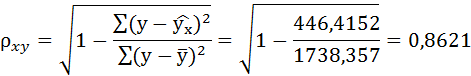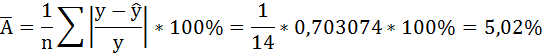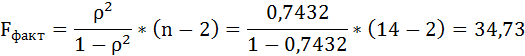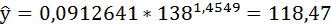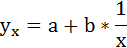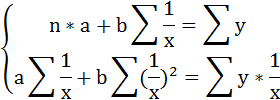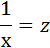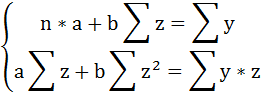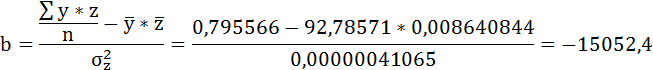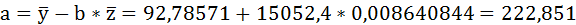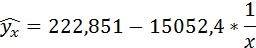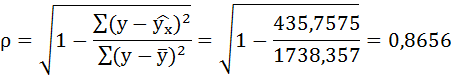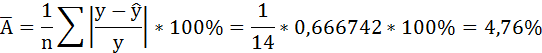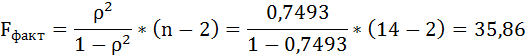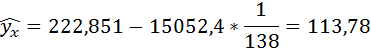Построить линейное уравнение парной регрессии y от x и объяснить его

Видео:Парная регрессия: линейная зависимостьСкачать

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 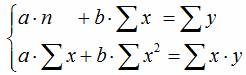. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

Видео:Эконометрика. Линейная парная регрессияСкачать

Парная линейная регрессия. Задачи регрессионного анализа

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Видео:Множественная регрессия в ExcelСкачать

Понятие линейной регрессии. Парная линейная регрессия

Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).

В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).

По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

— свободный член прямой парной линейной регрессии,

— коэффициент направления прямой парной линейной регрессии,

— случайная погрешность,

N — число элементов генеральной совокупности.

Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.

Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .

В результате получаем уравнение парной линейной регрессии выборки

— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,

— погрешность,

n — размер выборки.

Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде

.

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Уравнение парной линейной регрессии и метод наименьших квадратов

Определение коэффициентов уравнения парной линейной регрессии

Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:

.

Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:

• прямая парной линейной регрессии проходит через точку ;
• среднее значение отклонений равна нулю: ;
• значения и не связаны: .

Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:

,

.

Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).

Решение. Используем рассчитанные в решении названного выше примера суммы:

Используя эти суммы, вычислим коэффициенты:

Таким образом получили уравнение прямой парной линейной регрессии:

Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение

Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:

;

;

;

;

Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Анализ качества модели линейной регрессии

Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.

Коэффициент детерминации

Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:

,

— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,

— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,

— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.

Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.

F-статистика (статистика Фишера) для проверки качества модели линейной регрессии

Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

где m — число объясняющих переменных.

Сумма квадратов остатков

Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:

—

остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.

В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.

Стандартная ошибка регрессии

Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:

Чем меньше значение SEE, тем качественнее модель.

Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.

Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .

Можем убедиться, что выполняется закономерность SSR = SST — SSE :

Получаем коэффициент детерминации:

.

Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.

Видео:Парная нелинейная регрессияСкачать

Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной

Итак, уравнение парной линейной регрессии:

.

В этом уравнении a — свободный член, b — коэффициент при независимой переменной.

Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.

Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.

Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?

Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .

Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .

Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Задачи регрессионного анализа

Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.

Наиболее частые задачи регрессионного анализа:

• установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
• выявление причинных связей между переменными величинами;
• прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.

Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.

В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.

Видео:Множественная регрессияСкачать

Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии

Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.

Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.

рассматривают во взаимосвязи с альтернативной гипотезой

.

Статистика коэффициента направления

соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,

где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .

Доверительный интервал коэффициента направления прямой линейной регрессии:

.

Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:

Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.

Можем рассчитать, что , а стандартная погрешность регрессии .

Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :

.

Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:

.

Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Уравнение парной линейной регрессии

Если зависимость между результатом и фактором установлена, то ее целесообразно представить математической функцией y = f(x). При выборе типа функции (линейная или нелинейная) руководствуются характером расположения точек на поле корреляции, а также содержанием изучаемой связи, которая наилучшим образом соответствует исходным данным, иначе говоря, обеспечивает наилучшую аппроксимацию поля корреляции.

Когда влияние изменения фактора на результат постоянно, используют линейную функцию, в других случаях необходимо применять нелинейные функции.

Математическое описание зависимости в среднем изменений результативного признака у от фактора х называется уравнением парной регрессии.

Парная линейная регрессия имеет вид

где у_х — среднее значение результативного признака при определенном значении факторного признака х; а — свободный член уравнения регрессии; b — коэффициент регрессии.

Построение регрессионной модели включает следующие основные этапы:

• — определение цели исследования;
• — оценка однородности исходных данных;
• — выбор формы связи между результатом и отобранными факторами;
• — определение параметров модели;
• — оценка тесноты связи;
• — определение показателей эластичности;
• — проверка качества построенной модели.

Вернемся к рассматриваемому примеру 8.1 и построим уравнение парной линейной регрессии.

Вначале оценим однородность исходных данных, для чего рассчитаем коэффициент вариации (см. гл. 6):

Значение коэффициента вариации менее 30%, что говорит об однородности исходных данных, а следовательно, о возможности построения уравнения регрессии.

Найдем параметры а и b парной линейной регрессии у_х = а + Ьх.

Для этого используем метод наименьших квадратов (МНК). Исходное условие МНК:

Нужно подобрать такую прямую у_х = а + Ьх, которая отражает минимальность суммы квадратов отклонений фактических значений результативной переменной от ее теоретических значений, получаемых на основе уравнения регрессии.

Для этого воспользуемся системой нормальных уравнений МНК для прямой:

Решая эту систему, можно получить формулы для определения параметров а и Ъ:

отсюда

следовательно,

Используя расчетные данные табл. 8.2, получаем

Теперь можно записать уравнение парной регрессии:

Параметр а выполняет роль доводки до соотношения между средними признаками х и у, никакого экономического смысла в него не вкладывается. Параметр b (коэффициент регрессии) показывает, что в среднем с ростом накопленных за семестр баллов на одну единицу оценка растет на 0,069 балла.

Направление связи между признаками у и.г определяет знак коэффициента регрессии Ь. В нашем примере b > О, т.е. связь является прямой. Если b те — V т К,-

Когда единицы измерения исследуемых показателей различаются, для оценки влияния факторов па результативный признак вычисляют коэффициенты эластичности.

В нашем примере максимально возможное число баллов, которое можно получить на экзамене, равно 5, а максимально накопленное за семестр число баллов равно 100.

Средний коэффициент эластичности для парной линейной регрессии рассчитывается по формуле

Он показывает, па сколько процентов изменяется результативный признаку при изменении факторного признака на 1% от своего среднего значения.

В нашем примере

Это означает, что при увеличении накопленных за семестр баллов на 1% оценка за экзамен увеличивается примерно на 15%.

По уравнению у_х = -1,83 + 0,069# рассчитаем ожидаемые (теоретические) значения экзаменационной оценки для каждого студента (у_х ). Результаты представлены в табл. 8.3. Значения у. подтверждают, что найденная линия регрессии является наилучшей для аппроксимации исходных данных.

Отклонения фактических оценок от теоретических невелики. Для оценки этих отклонений рассчитывают ошибку аппроксимации. Средняя относительная ошибка аппроксимации определяется но формуле

Найдем ошибку аппроксимации для нашего примера. Для этого составим расчетную таблицу (табл. 8.3).

В нашем примере что говорит о хорошем качестве

уравнения регрессии, поскольку ошибка аппроксимации в пределах 6—10% свидетельствует о хорошем соответствии модели исходным данным.

В последней графе табл. 8.3 показаны квадраты отклонений фактических значений (у.) от расчетных (г/.).

Сумма является составляющей общей колеблемости г/,

которая в регрессионном анализе представлена следующим образом:

где — общая колеблемость; — остаточная колеблемость; ‘ — колеблемость у, объясненная уравнением регрессии.

Это разложение вариации зависимой переменной (формула (8.10)) лежит в основе оценки качества полученного уравнения регрессии: чем большая часть вариации у объясняется регрессией, тем лучше качество регрессии, т.е. правильно выбран тип функции для описания зависимости У = /(*), правильно выделена объясняющая переменная (признак-фактор) х.

Отношение объясненной вариации к общей вариации позволяет найти коэффициент детерминации

Этот коэффициент определяет степень детерминации регрессией вариации у.

Корень квадратный из коэффициента детерминации называется теоретическим корреляционным отношением, оно определяет тесноту связи между результативным и факторным признаками при линейной и нелинейной зависимости. Теоретическое корреляционное отношение изменяется от 0 до 1. Чем ближе его значение к 1, тем связь между признаками теснее.

В нашем примере

Отсюда , или 85%, что совпадает с ранее полученным

значением коэффициента детерминации.

В случае высокой детерминации (гр > 0,9) уравнение регрессии может использоваться для прогнозирования зависимой переменной. В этом случае можно предсказать ожидаемое значение у по уравнению регрессии на основе ожидаемого значения х.

В нашем примере уравнение регрессии позволяет определить ожидаемую экзаменационную оценку на основе суммы накопленных за семестр текущих баллов.

Выполнить регрессионный анализ, можно воспользовавшись ПК и пакетами прикладных программ Excel, EViews, Statgraphics, Statistica и т.д. Рассмотрим построение парной линейной регрессии с помощью Microsoft Office Excel 2007. Для этого надо произвести следующие действия.

• 1. Выбрать Данные —> Анализ данных —» Регрессия.
• 2. В диалоговом окне Регрессия сделать следующее:
  • — ввести в окне Редактирование Входной интервал Y диапазон зависимой переменной;
  • — ввести в окне Редактирование Входной интервал X диапазон факторной переменной;
  • — установить флажок Метки, если первая строка содержит название столбцов;
  • — установить флажок Константа-ноль, если в уравнении регрессии отсутствует свободный член а
  • — ввести в окне Редактирование Выходной интервал номер свободной ячейки на рабочем листе;
  • — нажать кнопку ОК.

В табл. 8.4 представлены результаты расчета с помощью Microsoft Office Excel:

• а) Регрессионная статистика’.
• — множественный R — коэффициент корреляции г_ху =0,92;

• — /^-квадрат — коэффициент детерминации г_ху =0,85;
• — наблюдения — число наблюдений п = 8;
• б) Дисперсионный анализ’.
• — столбец df— число степеней свободы.

Для строки Регрессия число степеней свободы определяется количеством параметров т в уравнении регрессии: df^ = т — 1.

В нашем примере два параметра: df^ = 2-1 = 1.

Регрессионный анализ: построение парной линейной регрессии с помощью Microsoft Office Excel 2007

Видео:Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

,

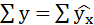
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмиро­вание степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наи­меньших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 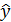. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz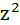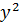
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.

📽️ Видео

Коэффициент линейной регрессии, 2 способаСкачать

Регрессия в ExcelСкачать

Математика #1 | Корреляция и регрессияСкачать

Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать

Парная и множественная линейная регрессияСкачать

МНК. Пример 2. Парная регрессияСкачать

Что такое линейная регрессия? Душкин объяснитСкачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать