Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров

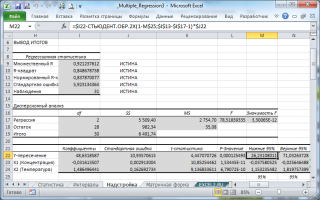
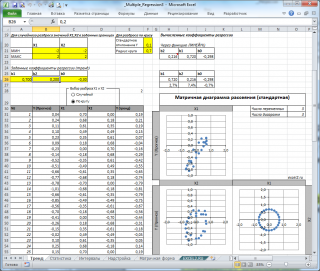
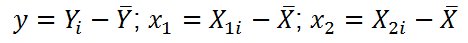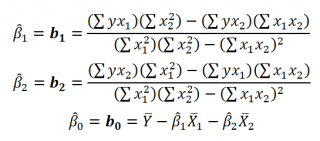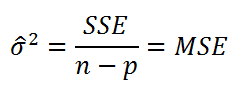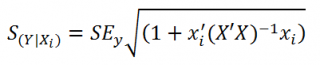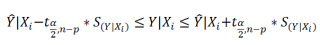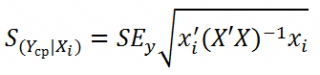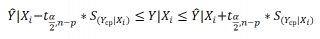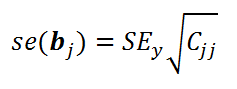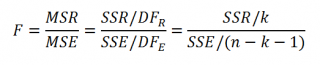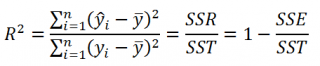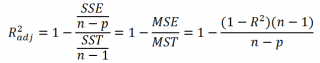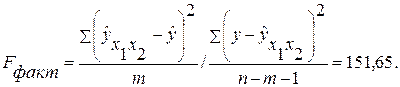Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
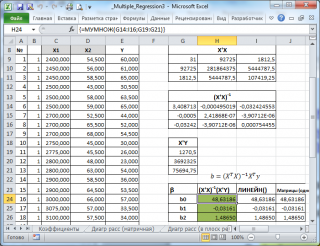
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Получили оценку уравнения регрессии: Y = 34.66 + 1.97X₁-2.45X₂
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 _e/∑(y_i — y_ср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X₁ (%), а также по уровню инфляции X₂ (%).

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:

1. Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
2. Рассчитать частные коэффициенты эластичности. Сделать вывод.
3. Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
4. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
5. Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.

Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

1	3.9	10
1	3.9	14
1	3.7	15
1	4	16
1	3.8	17
1	4.8	19
1	5.4	19
1	4.4	20
1	5.3	20
1	6.8	20
1	6	21
1	6.4	22
1	6.8	22
1	7.2	25
1	8	28
1	8.2	29
1	8.1	30
1	8.5	31
1	9.6	32
1	9	36

Матрица Y

7
7
7
7
7
7
8
8
8
10
9
11
9
11
12
12
12
12
14
14

Матрица X T

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x₁, x₂, x₃ взятых по отдельности. Для каждой объясняющей переменной:

1. Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
2. Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации.
3. Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
4. Постройте на поле корреляции прямую линию выборочной регрессии по точкам .
5. Постройте диаграмму остатков.
6. Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение F_табл определите с помощью функции FРАСПОБР).
7. Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
8. Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
9. Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
10. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

Множественная регрессия в EXCEL

history 26 января 2019 г.

Группы статей
• Статистический анализ

Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.

Перед прочтением этой статьи рекомендуется освежить в памяти простую линейную регрессию – прогнозирование на основе значений только одного фактора.

Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Множественного регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.

Статья про Множественный регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:

Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется множественной регрессией .

Множественная линейная регрессионная модель (Multiple Linear Regression Model) имеет вид Y=β ₀ +β ₁ *X ₁ +β ₂ *X ₂ +…+β _k *X _k +ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е. регрессоров . ε — случайная ошибка . Модель является линейной относительно неизвестных параметров β.

Оценка неизвестных параметров

В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.

Для описания зависимости Y от 2-х переменных линейная модель имеет вид:

Параметры этой модели β _i нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β ₀ , β ₁ , β ₂ ) обычно вычисляются методом наименьших квадратов (МНК) , который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).

Ошибка ε имеет случайную природу и имеет свою функцию распределения со средним значением =0 и дисперсией σ 2 .

Оценки b ₁ и b ₂ называются коэффициентами регрессии , они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются неизменными .

Сдвиг (intercept) или постоянный член b ₀ , определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто сдвиг не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями МНК ).

Вычислив оценки, полученные методом МНК, позволяют прогнозировать значения переменной Y:

Примечание : Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в плоскости регрессии ).

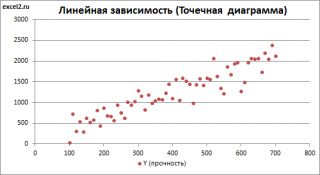
В качестве примера рассмотрим технологический процесс изготовления нити:

Инженер, на основе имеющегося опыта, предположил, что прочность нити Y зависит от концентрации исходного раствора (Х ₁ ) и температуры реакции (Х ₂ ), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.

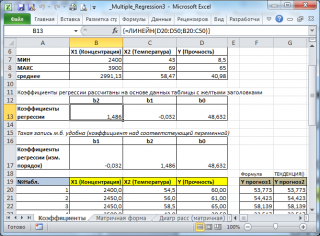
В MS EXCEL коэффициенты множественной регрессии удобнее всего вычислить с помощью функции ЛИНЕЙН() . Это сделано в файле примера на листе Коэффициенты . Чтобы вычислить оценки:

• выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2 коэффициента регрессии + величина сдвига = 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон С8:Е8 ;
• в Строке формул введите = ЛИНЕЙН(D20:D50;B20:C50) . Предполагается, что в столбце В содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах С и D содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D).
• нажмите CTRL+SHIFT+ENTER (т.к. это формула массива ).

В левой ячейке будет рассчитано значение коэффициента регрессии b 2 для переменной Х2, в средней ячейке — значение коэффициента регрессии b 1 для переменной Х1, в правой – сдвиг . Обратите внимание, что порядок вывода коэффициентов регрессии обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент b 2 располагается левее по отношению к b 1 , тогда как значения переменной Х2 располагаются правее значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17 файла примера .

Примечание : В принципе без функции ЛИНЕЙН() можно обойтись, записав альтернативные формулы. Для этого в файле примера на листе Коэффициенты в столбцах I : K вычислены отклонения значений переменных Х _1i , Х _2i , Y _i от их средних значений 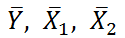, т.е.:

Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):

При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления коэффициентов регрессии значительно усложняются, поэтому следует использовать матричный подход.

В файле примера на листе Матричная форма выполнены расчеты коэффициентов регрессии с помощью матричного подхода.

Расчет можно произвести как пошагово, так и одной формулой массива :

Коэффициенты регрессии (вектор b ) в этом случае вычисляются по формуле b =(X T X) -1 (X T Y) или в другом виде записи b =(X ’ X) -1 (X ’ Y)

Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.

Диаграмма рассеяния

В случае простой линейной регрессии (один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят диаграмму рассеяния (двумерную).

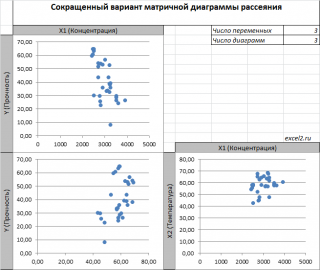
В случае множественной линейной регрессии двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См. файл примера лист Диагр расс (матричная) ).

К сожалению, такую диаграмму трудно интерпретировать.

Более того, матричная диаграмма может вводить в заблуждение (см. Introduction to linear regression analysis / D . C . Montgomery , E . A . Peck , G . G . Vining , раздел 3.2.5 ), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X _i и Y.

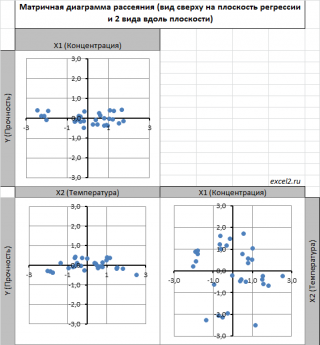
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной диаграммы рассеяния . В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно плоскости регрессии , то картину, на мой взгляд, будет проще интерпретировать.

Сравним две матричные диаграммы рассеяния (см. файл примера на листе «Диагр расс (в плоск регрессии)» , построенные для одних и тех же наблюдений. Первая – стандартная,

вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.

На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно провести процедуру F-теста ).

Несколько слов о построении альтернативной матричной диаграммы рассеяния:

• Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть среднее и разделить на стандартное отклонение ). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со стандартным нормальным распределением , 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
• Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти матрицу вращения , например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
• Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках Q31:S31 ).

Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов

После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.

Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:

Примечание: В MS EXCEL прогнозное значение Y для заданных Х ₁ и Х ₂ можно также предсказать с помощью функции ТЕНДЕНЦИЯ() . При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х ₁ и Х ₂ , а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х _1i и Х _2i ) для выбранного наблюдения i (см. файл примера, лист Коэффициенты, столбец G ). Функция ПРЕДСКАЗ() , использованная нами в простой регрессии, не работает в случае множественной регрессии .

Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить доверительный интервал этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.

Доверительные интервалы построим при фиксированном Х для:

• нового наблюдения Y;
• среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)

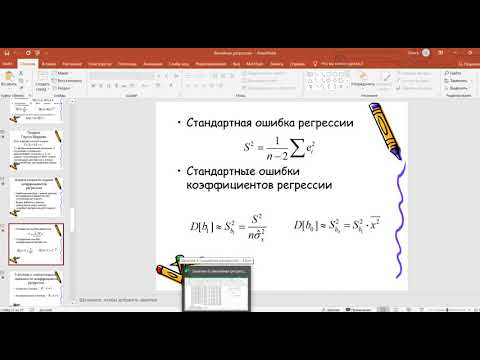
Как и в случае простой линейной регрессии , для построения доверительных интервалов нам потребуется сначала вычислить стандартную ошибку модели (standard error of the model) , которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.

Для вычисления стандартной ошибки оценивают дисперсию ошибки ε, т.е. сигма^2 (ее часто обозначают как MS Е либо MSres ) . Затем, вычислив из полученной оценки квадратный корень, получим Стандартную ошибку регрессии (часто обозначают как SEy или sey ).

где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi ( Sum of Squared Errors ). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).

Величина n-p – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае простой множественной регрессии с 2-мя регрессорами число степеней свободы равно n-3, т.к. при построении плоскости регрессии было оценено 3 параметра модели b (т.е. на это было «потрачено» 3 степени свободы ).

В MS EXCEL стандартную ошибку SEy можно вычислить формулы (см. файл примера, лист Статистика ):

Стандартная ошибка нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:

x _i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.

Соответствующий доверительный интервал вычисляется по формуле:

где α (альфа) – уровень значимости (обычно принимают равным 0,05=5%)

р – количество оцениваемых параметров модели (в нашем случае = 3)

n-p – число степеней свободы

– квантиль распределения Стьюдента (задает количество стандартных ошибок , в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если квантиль равен 2, то диапазон шириной +/- 2 стандартных ошибок относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) , подробнее см. в статье про распределение Стьюдента .

– прогнозное значение Yi вычисляемое по формуле Yi= b 0+ b 1* Х1i+ b 2* Х2i (точечная оценка).

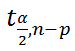
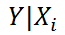
Стандартная ошибка среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:

x _i — вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.

Соответствующий доверительный интервал вычисляется по формуле:

Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.

Стандартные ошибки и доверительные интервалы для коэффициентов регрессии

В разделе Оценка неизвестных параметров мы получили точечные оценки коэффициентов регрессии . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ) коэффициентов регрессии .

Стандартная ошибка коэффициента регрессии b _j (обозначается se ( b _j ) ) вычисляется на основании стандартной ошибки по следующей формуле:

где C _jj является диагональным элементом матрицы (X ’ X) -1 . Для коэффициента сдвига b ₀ индекс j=1 (верхний левый элемент), для b ₁ индекс j=2, b ₂ индекс j=3 (нижний правый элемент).

SEy – стандартная ошибка регрессии (см. выше ).

В MS EXCEL стандартные ошибки коэффициентов регрессии можно вычислить с помощью функции ЛИНЕЙН() :

Примечание : Подробнее о функции ЛИНЕЙН() см. статью Функция MS EXCEL ЛИНЕЙН() .

Применяя матричный подход стандартные ошибки можно вычислить и через обычные формулы (точнее через формулу массива , см. файл примера лист Статистика ):

= КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))

При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:

где t – это t-значение , которое можно вычислить с помощью формулы = СТЬЮДЕНТ.ОБР.2Х(0,05;n-p) для уровня значимости 0,05.

В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии b _j . Здесь мы считаем, что коэффициент регрессии b _j имеет распределение Стьюдента с n-p степенями свободы (n – количество наблюдений, т.е. пар Х и Y).

Проверка гипотез

Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X, возможен, когда все коэффициенты регрессии β равны 0.

Чтобы убедиться, что вычисленная нами оценка коэффициентов регрессии не обусловлена лишь случайностью (они не случайно отличны от 0), используют проверку гипотез . В качестве нулевой гипотезы Н ₀ принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы Н ₁ принимают, что ХОТЯ БЫ ОДИН коэффициент β 0.

Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением дисперсионного анализа , использованного нами в случае простой линейной регрессии (F-тест) .

Если нулевая гипотеза справедлива, то тестовая F -статистика имеет F-распределение со степенями свободы k и n — k -1 , т.е. F _{k, n-k-1} :

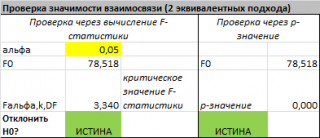
Проверку значимости регрессии можно также осуществить через вычисление p -значения . В этом случае вычисляют вероятность того, что случайная величина F примет значение F ₀ (это и есть p-значение ), затем сравнивают p-значение с заданным уровнем значимости α (альфа) . Если p-значение больше уровня значимости , то нулевую гипотезу нет оснований отклонить, и регрессия незначима.

В MS EXCEL значение F ₀ можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции ЛИНЕЙН() :

В MS EXCEL для проверки гипотезы через p -значение используйте формулу =F.РАСП.ПХ(F ₀ ;k;n-k-1) файл примера лист Статистика , где показано эквивалентность обоих подходов проверки значимости регрессии).

В MS EXCEL критическое значение для заданного уровня значимости F _{1-альфа, k, n-k-1} можно вычислить по формуле = F.ОБР(1- альфа;k;n-k-1) или = F.ОБР.ПХ(альфа;k; n-k-1) . Другими словами требуется вычислить верхний альфа- квантиль F -распределения с соответствующими степенями свободы .

Таким образом, при значении статистики F ₀ > F _{1-альфа, k, n-k-1} мы имеем основание для отклонения нулевой гипотезы.

В программах статистики результаты процедуры F -теста выводят с помощью стандартной таблицы дисперсионного анализа . В файле примера такая таблица приведена на листе Надстройка , которая построена на основе результатов, возвращаемых инструментом Регрессия надстройки Пакета анализа MS EXCEL .

Генерация данных для множественной регрессии с помощью заданного тренда

Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.

Для решения этой задачи нам потребуется:

• задать значения регрессоров в нужном диапазоне (значения переменных Х);
• задать коэффициенты регрессии ( b );
• задать тренд (вычислить значения Y= b₀ +b₁ * Х ₁ + b₂ * Х ₂ );
• задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)

Все вычисления выполнены в файле примера, лист Тренд для случая 2-х регрессоров. Там же построены диаграммы рассеяния .

Коэффициент детерминации

Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .

По определению коэффициент детерминации R 2 равен:

R 2 = Изменчивость объясненная моделью ( SSR ) / Общая изменчивость ( SST ).

Этот показатель можно вычислить с помощью функции ЛИНЕЙН() :

При добавлении в модель новой объясняющей переменной Х, коэффициент детерминации будет всегда расти. Поэтому, рост коэффициента детерминации не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.

Более подходящей статистикой, которая лишена указанного недостатка, является нормированный коэффициент детерминации (Adjusted R-squared):

где p – число независимых регрессоров (вычисления см. файл примера лист Статистика ).

Тема: Многомерный регрессионный анализ

1. Цель и содержание лабораторной работы.

В простой линейной регрессии рассматривалась взаимосвязь между независимой и зависимой переменными. Связь между двумя переменными часто позволяет точно предсказать значение зависимой переменной, если известно значение независимой переменной. Однако для точного прогнозирования зависимой переменной обычно требуется знать значения более чем одной независимой переменной. Регрессионные модели с несколькими независимыми переменными называются моделями многомерной регрессии.

Выборуравнения многомерной регрессии с наиболее подходящими для прогноза переменными проводится следующим образом:

1. Определение набора возможных независимых переменных.

2. Исключение переменных, не имеющих существенного отно-шения к решению поставленной задачи (если переменная характеризуется значительными ошибками измерения, дублирует другие независимые переменные (мультиколлинеарность), точные данные по ней недоступны);

3. Выбор окончательного вида уравнения с «наилучшими» независимыми переменными, при этом решается задача обеспечения наилучшего прогноза с наименьшими затратами.

Области применения многомерного регрессионного анализа различны:

— отражение взаимосвязи уровня зарплаты работников с географическим расположением компаний, уровнем безработицы в регионе, темпами роста промышленности, членством в союзах, отраслью промышленности или уровнем зарплаты в конкурирующих фирмах;

— анализ изменения цены на акции исходя из получаемых дивидендов, доходов от каждой акции, дробления акций, ожидаемой процентной ставки, объемов сбережений и уровня инфляции;

— исследование влияния на изменение мнения покупателей размеров рекламного бюджета, выбора средств информации, повторения информации, частоты рекламных акций или выбора рекламирующей персоны;

— анализ зависимости объема продаж от расходов на рекламу, уровня цен, маркетинговых расходов конкурентов и разовых заработков покупателей, а также от большого числа других переменных.

Таким образом, целью лабораторной работы является приобретение практических навыков построения уравнения многомерной регрессии предлагаемой социально-экономической ситуации с помощью инструмента анализа данных Excel.

2. Методические положения построения модели многомерной регрессии на основе практического примера.

В табл. 5.1 представлены исходные данные для проведения расчетов, где, Y – выработка продукции, — коэффициент обновления основных фондов, ₂ — доля рабочих высокой квалификации.

Необходимо ответить на следующие вопросы:

1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.

2. Проанализировать линейные коэффициенты парной и частной корреляции.

3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.

Исходные данные для многомерной регрессии

№ предприятия	y	x1	x2	№ предприятия	y	x1	x2
3,9
3,9	6,4
3,7	6,8
7,2
3,8
4,8	8,2
5,4	8,1
4,4	8,5
5,3	9,6
6,8

4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и . Сравнить значения скорректированного и нескорректированного коэффициентов множественной детерминации.

5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после .

6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

Решение с помощьюExcel .

1.Дляоценки показателя вариации каждого признака необходимо составить сводную таблицу основных статистических характеристик для одного или нескольких массивов данных, которую можно получить с помощью инструмента анализа данных, Описательная статистика.Для этого следует выполнить следующие шаги:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

в главном меню выберите последовательно пункты Сервис/Анализ данных/Описательная статистика, после чего щелкните по кнопке OK;

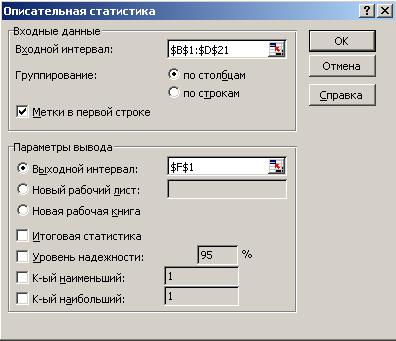
2) заполните диалоговое окно ввода данных и параметров вывода (рис. 5.1).

Рис. 5.1. Диалоговое окно ввода параметров инструмента

Входной интервал – диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов).

Группирование – по столбцам или строкам – необходимо указать дополнительно.

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет.

Выходной интервал – достаточно указать верхнюю левую ячейку будущего диапазона.

Новый рабочий лист — можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию по итоговой статистике, уровню надежности, k-го наибольшего и наименьшего значений, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке OK.

Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 5.2.

Рис. 5.2. Результат применения инструмента Описательная статистика

Сравнивая значения средних квадратических σ_y, σ_x1, σ_x21 отклонений и средних величин , и определяя коэффициенты вариации, приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%.

;

;

.

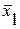
Следовательно, совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

К сожалению, в ППП Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция.Для этого:

1) в главном меню последовательно выберите пункты Сервис/ Анализ данных/ Корреляция.Щелкните по кнопке OK;

2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 1.1);

3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рис. 5.3.

Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки y как с коэффициентом обновления основных фондов — , так и с долей рабочих высокой квалификации — ( и ). Но в то же время, межфакторная связь весьма тесная и превышает тесноту связи с y. В связи с этим для улучшения данной модели можно исключить из нее фактор как малоинформативный, недостаточно статистически надежный.

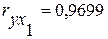
Рис. 5.3. Матрица коэффициентов парной корреляции

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции.Если сравнивать коэффициенты парной и частной корреляции, можно сказать, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи, именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

3. Вычисление параметров линейного уравнения множественной регрессии.

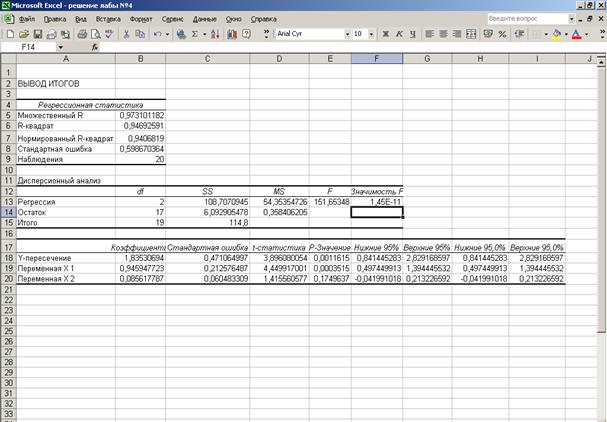
Эта операция проводится с помощью инструмента анализа данных Регрессия.Она аналогична расчету параметров парной линейной регрессии, а отличие от парной регрессии состоит только в том, что в диалоговом окне при заполнении параметров входной интервал Х следует указывать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 5. 4.

Рис. 5.4. Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии вида

;

.

Величина оценивает агрегированное влияние прочих (кроме учтенных в модели факторов и ) факторов на результат y. Величины и указывают, что с увеличением и на единицу результат увеличивается соответственно на 0,9459 и 0,0856 млн. руб. Сравнивать эти значения не следует, т.к. они зависят от единиц измерения каждого признака и потому несопоставимы между собой.

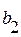
Значения случайных ошибок параметров , и с учетом округления составят: , , . Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента ; ; .

Если значения t — критерия больше 2 — 3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются и , а величина сформировалась под воздействием случайных причин, поэтому фактор , силу влияния которого оценивает , можно исключить как несущественно влияющий, неинформативный.

На это же указывает показатель вероятности случайных значений параметров регрессии: если 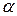меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%, 5% или 1% вероятности), делают вывод о несущественной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уровня. Здесь > 5%, что позволяет рассматривать как неинформативный фактор и удалить его для улучшения данного уравнения.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает F-критерий Фишера:

По данным таблицы дисперсионного анализа, представленной на рис. 5.4, =151,65. Вероятность случайно получить такое значение F-критерия составляет 0 (см. значимость F), что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина Р — значение из этой же таблицы. Следовательно, полученное значение неслучайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 5. 4 в рамках регрессионной статистики. Нескорректированный коэффициент множественной детерминации 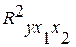=0,9469 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации 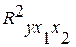=0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами и .

5. Информация для оценки с помощью частных F- критериев Фишера целесообразности включения в модель фактора после фактора и фактора после фактора может быть получена в ППП Statgraphics. Частный F- критерий показывает статистическую значимость включения фактора после того, как в нее включен фактор .

Но по данным, вычисленным с помощью ППП Excel, можно сделать общий вывод, который состоит в том, что множественная модель с факторами и с =0,9469 содержит неинформативный фактор . Если исключить фактор , то можно ограничиться уравнением парной регрессии более простым, хорошо детерминированным, пригодным для анализа и для прогноза.

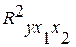
6. Средние частные коэффициенты эластичности показывают, на сколько процентов от значения своей средней изменяется результат при изменении фактора на 1% от своей средней и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости

, (5.1)

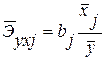
где — коэффициент регрессии при в уравнении множественной регрессии.

Здесь ,

.

По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора , чем признака фактора : 0,6% против 0,2%.

3. Задание лабораторной работы.

В предлагаемых по вариантам задачах необходимо составить прогноз социально-экономического развития анализируемого показателя по методу многомерной регрессии, используя последовательность аналитических расчетов представленного практического примера.

Вариант 1.

По исходным данным, представленным в табл. 5.2, определить возможность выбора определенного кандидата на должность менеджера по продажам на основе предлагаемых независимых переменных. В качестве зависимой переменной предлагается выбрать объем продаж за месяц рассматриваемого менеджера.

Объем продаж за месяц (в единицах) Y	Результат теста способностей X1	Возраст X2	Результат теста тревожности X3	Опыт работы X4	Средний балл школьного аттестата X5
22,1	4,9	2,4
22,5	3,0	2,6
23,1	1,5	2,8
0,6	2,7
22,6	1,8	2,0
21,7	3,3	2,5
3,2	2,5
22,4	2,1	2,3
22,6	6,0	2,8
21,1	1,8	3,4
22,5	3,8	3,0
22,2	4,5	2,7
24,8	4,5	2,8
24,8	0.1	3,8
22,6	0,9	3,7
20,5	4,8	2,1
21,9	2,3	1,8

Вариант 2.

Необходимо составить прогноз времени, затрачиваемого персоналом на обслуживание одного покупателя, используя такие независимые переменные, как количество приобретаемых единиц товара и общая стоимость покупок. Для составления прогноза представлены данные по выборке из 18 покупателей, представленные в табл. 5. 2.

Определите лучшее уравнение регрессии для предлагаемых данных. Составьте прогноз времени обслуживания покупателя, приобретающего 14 единиц товара общей стоимостью 70 ден. ед.

Покупатель	Время обслуживания (мин.), Y	Стоимость покупок (ден. ед.), X1	Количество единиц товара, X2
3,0
1,3
0,5
7,4
5,9
8,4
5,0
8,1
1,9
6,2
0,7
1,4
9,1
0,9
5,4
3,3
4,5
2,4

Вариант 3.

С целью прогнозирования годового объема продаж запчастей к автомобилям в регионе собраны статистические данные, представленные в табл. 5.4. Необходимо составить прогноз, используя в качестве независимых переменных количество пунктов розничной торговли в конкретном регионе, количество автомобилей и доход населения.

Спрогнозируйте годовой объем продаж для региона 12 с 2500 пунктами обслуживания и 20,2 млн. ден. ед. зарегистрированных автомобилей и доходом населения 40 млрд. ден. ед.

Регион	Годовой объем продаж (млн. ден. ед.), Y	Количество пунктов обслуживания, X1	Количество зарегистрированных автомобилей, X2	Общий доход населения (млрд. ден. ед.), X2
52,3	24,6	98,5
26,0	22,1	31,1
20,2	7,9	34,8
16,0	12,5	32,7
30,0	9,0	68,8
46,2	11,5	94,7
35,0	20,5	67,6
3,5	4,1	19,7
33,1	8,9	67,9
25,2	6,1	61,4
38,2	9,5	75,6

1. Андронова, И.В. Социальное и экономическое прогнозирование. [Текст]: методические указания по изучению курса и самостоятельной работе студентов очной и заочной форм обучения специальностей 080502 «Экономика и управление на предприятии отраслей ТЭК»/ И.В.Андронова, Е.Г. Кульчихина, Е.Л. Чижевская – Тюмень: ТюмГНГУ, 2003.

2. Андронова, И. В. Методология формирования управленческих решений на основе экспертного оценивания [Текст]: учеб. пособие/ И.В. Андронова, И.В.Осиновская – Тюмень: ТюмГНГУ, 2004. – 122 с.

3. Андронова, И.В. Социально-экономическое прогнозирование (в схемах и таблицах) [Текст]: учебно-практическое пособие/ И.В. Андронова, В.В. Пленкина, И.В.Осиновская – Тюмень: ТюмГНГУ, 2005. – 155 с.

4. Андронова, И.В. Социально-экономическое прогнозирование: практикум (в схемах и таблицах) [Текст]: учебное пособие/ И.В. Андронова, В.В. Пленкина, И.В. Осиновская – Тюмень: ТюмГНГУ, 2007. – 105 с.

5. Дуброва, Т.А. Статистические методы прогнозирования [Текст]: учебное пособие для вузов/ Т.А. Дуброва – М.: ЮНИТИ – Дана, 2003. – 206 с.

6. Сулицкий, В.М. Методы статистического анализа в управлении [Текст]: учеб. пособие/ В. М. Сулицкий – М.: Дело, 2002. – 520 с.

7. Ханк, Д.Э. Бизнес- прогнозирование [Текст]/ Д.Э. Ханк, Д.У. Уичерн, А. Дж. Райтс; пер. с англ. – Изд. 7-е. — М.: Издательский дом «Вильямс», 2003. — 656 с.

Исходные данные для выполнения лабораторной работы №1

№ вари­ант	Показатель	Условные годы
Добыча нефти, тыс.т	273,1	295.2	312,6	365,8	389,9	403,4	408,6	397,8	367,9
Объем бурения, млн.м	6,7	8,3	14,3	18,0	22,7	26,0	28,8	28,2	25,2
Скорость бурения, м/ст-мес.
Средняя глубина скважин, тыс. м	2,05	2,25	2,40	2,48	2,52	2,53	2,55	2,55	2,56
Коэффициент эксплуатации нефтяных скважин, доли	0,940	0,945	0,952	0,928	0,946	0,944	0,945	0,944	0,942
6	Действующий фонд газовых скважин, скв.
Ввод в эксплуатацию новых скважин, скв.
Добыча газа, млрд. м З	20,3	22,0	23,6	25,2	28,8	28,9	30,8	31,9	32,5
Проходка на 1 бур. бригаду, тыс. м	34,4	53,0	43,2	48,9	54,3	57,2	62,7	62,4	58,8
Среднесуточный дебит скважин, т	105,8	125,4	94,3	43,9	36,6	31,2	26.2	22.2	18,7
Объем перекачки газа, млрд. м 3
Средняя дальность транспортировки нефти, тыс. км	1,24	1,34	1,46	1,60	1,70	1,85	1,97	2,07	2,16
Протяженность магистральных газопроводов, тыс. км
Коммерческая скорость, м/ст.-мес.
Объем реализации нефтепродуктов тыс. т

Квантиль распределения Стьюдента

p k	0,900	0,950	0,975	0,990	0,995
3,078	6,314	12,706	31,821	63,657
1,886	2,920	4,303	6,965	9.925
1,638	2,353	3,182	4,541	5,841
1,533	2,132	2,776	3,747	4,604
1,476	2,015	2,571	3,365	4,032
1,440	1,943	2,447	3,143	3,707
1,415	1,895	2,365	2,998	3,499
1,397	1,860	2,306	2,896	3,355
1,383	1,833	2,262	2,821	3,250
1,372	1,812	2,228	2,764	3,169
1,363	1,796	2,201	2,718	3,106
1,356	1,782	2,179	2,681	3,055
1,350	1,771	2,160	2,650	3,012
1,345	1,761	2,145	2,624	2,977
1,341	1,753	2,131	2,602	2,947
1,337	1,746	2,120	2,583	2,921
1,333	1,740	2,110	2,567	2,898
1,330	1,734	2,101	2,552	2,878
1,328	1,729	2,093	2,539	2,861
1,325	1,725	2,086	2,528	2,845
1,316	1,708	2,060	2,485	2,787
1,310	1,697	2,042	2,457	2,750
1,306	1,690	2,030	2,438	2,724
1,303	1,684	2,021	2,423	2,704
1,301	1,679	2,014	2,412	2,690
1,299	1,676	2,009	2,403	2,678
1,297	1,673	2,004	2,396	2,670
1,296	1,671	2,000	2,390	2,660
1,294	1,667	1,994	2,381	2,648
1,292	1,664	1,990	2,374	2,639
1,291	1,662	1,987	2,368	2,632
1,290	1,660	1,984	2,364	2,626

СОДЕРЖАНИЕ

Общие положения по выполнению лабораторных работ……………………4

Лабораторная работа № 2 ………………………………………………. 12

Лабораторная работа № 4 ……………………………………………………21

Лабораторная работа № 5 ……………………………………………………44

Карнаухов Максим Николаевич

Осиновская Ирина Владимировна

Шарипова Анастасия Евгеньевна

СОЦИАЛЬНОЕ И ЭКОНОМИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ:

Множественная линейная регрессия

Задачей множественной линейной регрессии является построение линейной модели связи между набором непрерывных предикторов и непрерывной зависимой переменной. Часто используется следующее регрессионное уравнение:

(1)

Здесь а_i — регрессионные коэффициенты, b₀ — свободный член(если он используется), е — член, содержащий ошибку — по поводу него делаются различные предположения, которые, однако, чаще сводятся к нормальности распределения с нулевым вектором мат. ожидания и корреляционной матрицей .

Такой линейной моделью хорошо описываются многие задачи в различных предметных областях, например, экономике, промышленности, медицине. Это происходит потому, что некоторые задачи линейны по своей природе.

Приведем простой пример. Пусть требуется предсказать стоимость прокладки дороги по известным ее параметрам. При этом у нас есть данные о уже проложенных дорогах с указанием протяженности, глубины обсыпки, количества рабочего материала, числе рабочих и так далее.

Ясно, что стоимость дороги в итоге станет равной сумме стоимостей всех этих факторов в отдельности. Потребуется некоторое количество, например, щебня, с известной стоимостью за тонну, некоторое количество асфальта также с известной стоимостью.

Возможно, для прокладки придется вырубать лес, что также приведет к дополнительным затратам. Все это вместе даст стоимость создания дороги.

При этом в модель войдет свободный член, который, например, будет отвечать за организационные расходы (которые примерно одинаковы для всех строительно-монтажных работ данного уровня) или налоговые отчисления.

Ошибка будет включать в себя факторы, которые мы не учли при построении модели (например, погоду при строительстве — ее вообще учесть невозможно).

Пример: множественный регрессионный анализ

Для этого примера будут анализироваться несколько возможных корреляций уровня бедности и степень, которая предсказывает процент семей, находящихся за чертой бедности. Следовательно мы будем считать переменную характерезующую процент семей, находящихся за чертой бедности, — зависимой переменной, а остальные переменные непрерывными предикторами.

Коэффициенты регрессии

Чтобы узнать, какая из независимых переменных делает больший вклад в предсказание уровня бедности, изучим стандартизованные коэффициенты (или Бета) регрессии.

Рис. 1. Оценки параметров коэффициентов регрессии.

Коэффициенты Бета это коэффициенты, которые вы бы получили, если бы привели все переменные к среднему 0 и стандартному отклонению 1. Следовательно величина этих Бета коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в зависимую переменную. Как видно из Таблицы, показанной выше, переменные изменения населения с 1960 года (POP_ CHING), процент населения, проживающего в деревне (PT_RURAL) и число людей, занятых в сельском хозяйстве (N_Empld) являются самыми главными предикторами уровня бедности, т.к. только они статистически значимы (их 95% доверительный интервал не включает в себя 0). Коэффициент регрессии изменения населения с 1960 года (Pop_Chng) отрицательный, следовательно, чем меньше возрастает численность населения, тем больше семей, которые живут за чертой бедности в соответствующем округе. Коэффициент регрессии для населения (%), проживающего в деревне (Pt_Rural) положительный, т.е., чем больше процент сельских жителей, тем больше уровень бедности.

Значимость эффектов предиктора

Просмотрим Таблицу с критериями значимости.

Рис. 2. Одновременные результаты для каждой заданной переменной.

Как показывает эта Таблица, статистически значимы только эффекты 2 переменных: изменение населения с 1960 года (Pop_Chng) и процент населения, проживающего в деревне (Pt_Rural), p

🎥 Видео