Построить конус второго порядка по уравнению

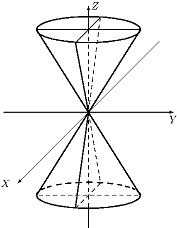
Конусом второго порядка называется поверхность, заданная относительно специально выбранной системы координат уравнением x 2 /a 2 +y 2 /b 2 -z 2 /c 2 =0 (1). Из уравнения конуса второго порядка следует, что, если точка с координатами (x, y, z) лежит на этой поверхности, то на этой поверхности лежит и точка (±x, ±y, ±z) при любом наборе знаков + и -. Следовательно, координатные плоскости являются плоскостями симметрии конуса второго порядка.

Будем считать, что a≥b. 1) Если a=b, то конус второго порядка называется конусом вращения и получается вращением вокруг оси oz двух пересекающихся прямых y/b-z/c=0 и y/b+z/c=0. 2) Пусть a>b. Начало координат называют вершиной конуса второго порядка. Ось oz — осью симметрии конуса.

Основное свойство конуса: если точка M₀(x₀, y₀, z₀) лежит на конусе второго порядка, то и вся прямая OM₀ также лежит на нем, где O — вершина конуса, точка M₀ отлична от вершины конуса.

Конус второго порядка, заданный уравнением (1) определяет собой поверхность, образованную следующим образом: каждая точка эллипса x 2 /(ac/h) 2 +y 2 /(bc/h) 2 =1 соединяется с началом координат по прямым.

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Видео:Поверхности второго порядкаСкачать

Построить конус второго порядка по уравнению

Из уравнения следует, что |z| > c. Пересечениями поверхности с плоскостями z = h, |h| > c, являются эллипсы: . полуоси которых увеличиваются с ростом |h|. Сечением плоскостью x = 0 является гипербола: . фокусы которой лежат на оси OZ. При . двуполостный гиперболоид можно получить, вращая эту гиперболу вокруг оси OZ.

В сечениях плоскостями z = h получаются эллипсы, полуоси которых увеличиваются с ростом |h|. Только при h = 0 получается одна точка — вершина конуса. Если a = b, то эти эллипсы являются окружностями и конус называется прямым круговым. Пересекая конус плоскостью x = 0, получим две пересекающиеся прямые . Другие сечения конической поверхности мы рассматривали в пункте 8.1.4, изучая кривые 2-го порядка. Каноническое уравнение:

Замечание. Обратим внимание: однополостный, двуполостный гиперболоиды и конус задаются похожими уравнениями. Можно рассмотреть более общее уравнение, включающее все 3 возможности:

Проследим, как меняется поверхность при изменении h. При h > 0 это однополостный гиперболоид. Уменьшая h, мы уменьшаем размеры наименьшего эллипса в его сечении. Гиперболы приближаются к своим асимптотам, их вершины сближаются. При h = 0 гиперболоид превращается в

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Поверхности второго порядка

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Поверхности вращения.

Поверхность (S) называется поверхностью вращения с осью (d), если она составлена из окружностей, которые имеют центры на прямой (d) и лежат в плоскостях, перпендикулярных данной прямой.

Рассмотрим линию (L), которая лежит в плоскости (P), проходящей через ось вращения (d) (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.

Рис. 10.1. Поверхность вращения.

Выберем начало декартовой прямоугольной системы координат (O, boldsymbol_, boldsymbol_, boldsymbol_) на оси (d), вектор (boldsymbol_) направим вдоль (d), а вектор (boldsymbol_) поместим в плоскости (P). Таким образом, (O, boldsymbol_, boldsymbol_) — декартова система координат в плоскости (P). Пусть линия (L) имеет в этой системе координат уравнение (f(x, y)=0).

Рассмотрим точку (M(x, y, z)). Через нее проходит окружность, которая имеет центр на оси (d) и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от (M) до оси, то есть (sqrt<x^+y^>). Точка (M) лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии (L).

Точка (M_(x_, y_, z_)) лежит в плоскости (P), и потому (y_=0). Кроме того, (z_=z) и (|x|=sqrt<x^+y^>), так как (M_) лежит на той же окружности, что и (M). Координаты точки (M_) удовлетворяют уравнению линии (L): (f(x_, z_)=0). Подставляя в это уравнение (x_) и (z_), мы получаем условие на координаты точки (M), необходимое и достаточное для того, чтобы (M) лежала на поверхности вращения (S): равенство
$$
fleft(pm sqrt<x^+y^>, zright)=0label
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
fleft(sqrt<x^+y^>, zright)fleft(-sqrt<x^+y^>, zright)=0,label
$$
и является уравнением поверхности вращения линии (L) вокруг оси (d).

Видео:Поверхности 2 порядкаСкачать

Эллипсоид.

Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор (boldsymbol_) сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
frac<x^><a^>+frac<z^><c^>=1, frac<z^><a^>+frac<x^><c^>=1.nonumber
$$
(Здесь через (c) обозначена малая полуось эллипса.) В силу формулы eqref уравнениями соответствующих поверхностей вращения будут
$$
frac<x^+y^><a^>+frac<z^><c^>=1, frac<z^><a^>+frac<x^+y^><c^>=1 (a > c).label
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).

Рис. 10.2. Сжатый (а) и вытянутый (б) эллипсоиды вращения.

Каждую точку (M(x, y, z)) на сжатом эллипсоиде вращения сдвинем к плоскости (y=0) так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении (lambda Рис. 10.3. Эллипсоид.

Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения eqref видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.

Эллипсоид можно получить из сферы (x^+y^+z^=a^) сжатиями к плоскостям (y=0) и (z=0) в отношениях (lambda=b/a) и (mu=c/a).

В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.

Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Конус второго порядка.

Рассмотрим на плоскости (P) пару пересекающихся прямых, задаваемую в системе координат (O, boldsymbol_, boldsymbol_) уравнением (a^x^-c^z^=0). Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^(x^+y^)-c^z^=0label
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости (y=0) переводит прямой круговой конус в поверхность с уравнением
$$
a^x^+b^y^-c^z^=0label
$$
называемую конусом второго порядка.

Обратите внимание на то, что левая часть уравнения eqref — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.

Рис. 10.4. Прямой круговой конус.

Видео:Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Однополостный гиперболоид.

Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
frac<x^><a^>-frac<z^><c^>=1nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле eqref мы получаем уравнение этой поверхности (рис. 10.5)
$$
frac<x^+y^><a^>-frac<z^><c^>=1.label
$$

Рис. 10.5. Однополостный гиперболоид вращения.

В результате сжатия однополостного гиперболоида вращения к плоскости (y=0) мы получаем однополостный гиперболоид с уравнением
$$
frac<x^><a^>+frac<y^><b^>-frac<z^><c^>=1.label
$$

Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.

Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность (x^+y^-z^=0) и точку (M_(1, 1, 1)) на ней. Подставляя координаты (M_) в уравнения eqref, мы получаем условия на (lambda) и (mu): (2lambda=2mu) и (0 cdot lambda=0 cdot mu). Первое из них определяет (lambda) и (mu) с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в eqref, получаем уравнения прямолинейной образующей
$$
x+z=1+y, x-z=1-y.nonumber
$$

Она проходит через (M_), так как (lambda) и (mu) так и выбирались, чтобы координаты (M_) удовлетворяли этой системе. Аналогично, подставляя координаты (M_) в (10), находим условия на (lambda’) и (mu’): (2mu’=0) и (2mu’=0). Коэффициент (lambda’) можно взять любым ненулевым, и мы приходим к уравнению второй образующей: (x=z), (y=1).

Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.

Видео:Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Двуполостный гиперболоид.

Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
frac<z^><c^>-frac<x^><a^>=1nonumber
$$
вокруг той оси, которая ее пересекает. По формуле eqref мы получаем уравнение двуполостного гиперболоида вращения
$$
frac<z^><c^>-frac<x^+y^><a^>=1.label
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
frac<z^><c^>-frac<x^><a^>-frac<y^><b^>=1.label
$$

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида eqref, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.

Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.

Рис. 10.6. Двуполостный гиперболоид вращения.

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Эллиптический параболоид.

Вращая параболу (x^=2pz) вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^+y^=2pz.label
$$
Она называется параболоидом вращения. Сжатие к плоскости (y=0) переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
frac<x^><a^>+frac<y^><b^>=2z.label
$$

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).

Рис. 10.7. Эллиптический параболоид.

Видео:Поверхности 2го порядка. КлассификацияСкачать

Гиперболический параболоид.

По аналогии с уравнением eqref мы можем написать уравнение
$$
frac<x^><a^>-frac<y^><b^>=2z.label
$$

Поверхность, которая имеет уравнение вида eqref в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.

Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью (x=alpha) при произвольном (alpha). В этой плоскости выберем декартову прямоугольную систему координат (O’, boldsymbol_, boldsymbol_) с началом в точке (O'(alpha, 0, 0)). Относительно этой системы координат линия пересечения имеет уравнение
$$
-frac<y^><b^>=2left(z-frac<alpha^><2a^>right).label
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку (O″) с координатами ((0, alpha^/(2a^))). (Координаты этой точки относительно исходной системы координат (O, boldsymbol_, boldsymbol_, boldsymbol_) в пространстве равны ((alpha, 0, alpha^/(2a^))).)

Точка (O″), очевидно, является вершиной параболы, ось параболы параллельна вектору (boldsymbol_), а знак минус в левой части равенства eqref означает, что ветви параболы направлены в сторону, противоположную направлению (boldsymbol_). Заметим, что после переноса начала координат в точку (O″) величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями (x=alpha) при всех (alpha) представляют собой равные параболы.

Будем теперь менять величину (alpha) и проследим за перемещением вершины параболы (O″) в зависимости от (alpha). Из приведенных выше координат точки (O″) следует, что эта точка перемещается по линии с уравнениями
$$
z=frac<x^><2a^>, y=0nonumber
$$
в системе координат (O, boldsymbol_, boldsymbol_, boldsymbol_). Эта линия — парабола в плоскости (y=0). Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор (boldsymbol_).

Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.

При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).

Рис. 10.8. Гиперболический параболоид. (OB) — неподвижная парабола, (KLM, NOP, QRS) — положения подвижной параболы.

Сечения гиперболического параболоида плоскостями с уравнениями (z=alpha) при всевозможных (alpha) — гиперболы. Эти сечения нарисованы на рис. 10.9.

Рис. 10.9. Сечения гиперболического параболоида

Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.

Рис. 10.10. Прямолинейные образующие гиперболического параболоида

🎥 Видео

ЗАДАНИЕ 2 ЕГЭ (ПРОФИЛЬ). КОНУС.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Кривые второго порядкаСкачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Кривые второго порядкаСкачать

Поворот и параллельный перенос координатных осей. ЭллипсСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать