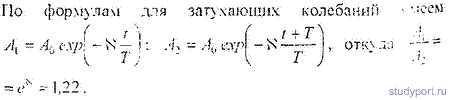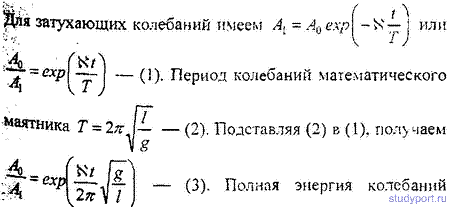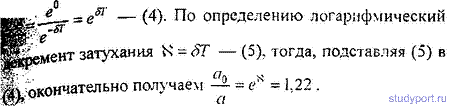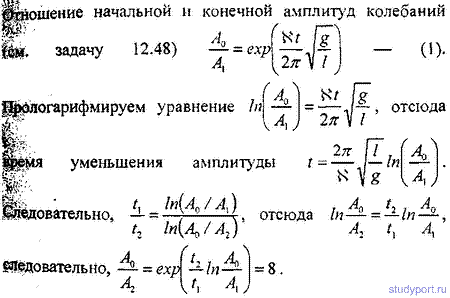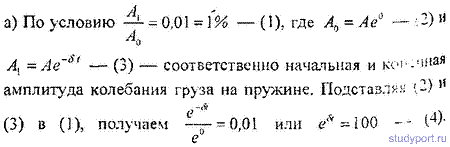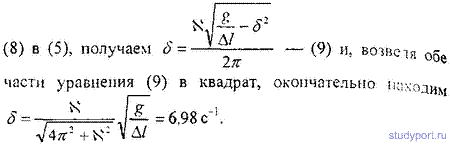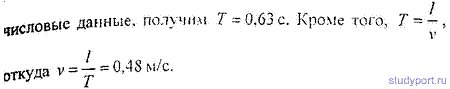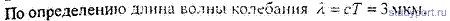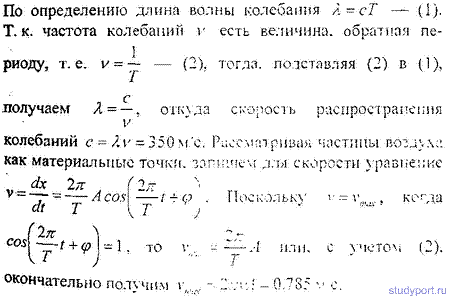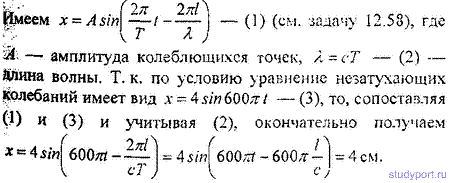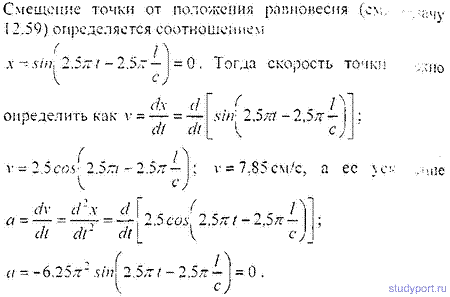Построить график затухающих колебаний данного уравнения (7 видео)

Затухающие колебания

Содержание

Определение затухающих колебаний
Уравнение колебаний пружинного маятника с затуханием
Диссипация энергии при затухающих колебаниях
Время жизни колебаний. Период затухающих колебаний. Декремент затухания
Примеры задач с решением
Гармоническое колебательное движение и волны
Построить график, затухающего колебания, данного уравнением x=5e-0,1t sin(π/4t) м
Ваш ответ
решение вопроса
Похожие вопросы
📹 Видео

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Определение затухающих колебаний

Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.

Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.

Видео:70. Затухающие колебанияСкачать

Уравнение колебаний пружинного маятника с затуханием

Иногда, если тело движется в веществе, силу сопротивления ($<overline>_

$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($overline$):

[<overline>_

=-beta overlineleft(1right),]

где $beta $ — коэффициент сопротивления.

Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:

где $dot=v_x.$ Принимая во внимание равенства:

(где $_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $gamma $=0) той же колебательной системы; $gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:

Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).

Уравнение затухающих колебаний имеет точное решение:

где $omega =sqrt<^2_0-^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $varphi $ — постоянная из начальных условий. При $gamma ll _0$, $omega approx _0$, параметр $A_0e^$ можно считать медленно изменяющейся во времени амплитудой колебаний.

Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Диссипация энергии при затухающих колебаниях

Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.

Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:

[frac

=-fracleftlangle E_krightrangle left(6right),]

где $frac

$ — скорость изменения энергии колебаний; $leftlangle E_krightrangle $ — средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.

Так как мы считаем затухание малым, то $leftlangle E_krightrangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:

[leftlangle E_krightrangle =fracleft(7right).]

В таком случае уравнение (6) можно записать в виде:

Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:

где $E_0$ — величина энергии колебательной системы в начальный момент времени.

Так как энергия колебаний пропорциональна квадрату амплитуды ($Esim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:

$A_0$ — начальная амплитуда колебаний.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Время жизни колебаний. Период затухающих колебаний. Декремент затухания

Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $tau =frac$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($tau gg T$). За время жизни происходит много колебательных движений.

Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.

Период затухающих колебаний считают равным:

Пусть $Aleft(tright) и A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:

называют декрементом затухания. Натуральный логарифм декремента затухания ($theta $):

называют логарифмическим декрементом затухания. Для колебательной системы $theta $ постоянная величина.

Видео:Как построить график гармонического колебанияСкачать

Примеры задач с решением

Задание. Каков коэффициент затухания маятника ($gamma $), если за $Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?

Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:

По условию задачи имеем:

С другой стороны:

где $t_2-t_1=Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:

Выразим $gamma $ из (1.3) учтем, что $frac =n$:

Ответ. $gamma =frac<>$

Задание. Что представляет собой фазовая траектория затухающего колебания?

Решение. Фазовой траекторией называют траекторию движения в плоскости $left(x;;vright).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $left(x,vright),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:

Фазовая траектория затухающего колебания, если

[<overline>_

=-beta overlineleft(2.2right),]

представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.

Видео:Урок 346. Определение добротности по графику затухающих колебаний Скачать

Гармоническое колебательное движение и волны

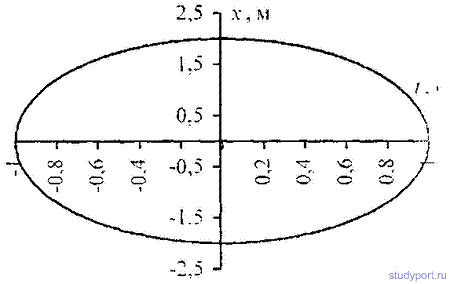
12.41. Точка участвует в двух взаимно перпендикулярных колебаниях x = sinPt и y = 2sin(Pt+P/2). Найти траекторию результирующего движения точки.

12 42. Точка участвует в двух взаимно перпендикулярных колебаниях х = sinPt a y = 4sin(Pt + P). Найти траекторию результирующего движения точки и начертить ее с нанесением масштаба.

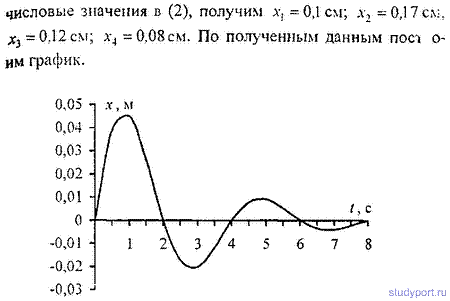
12.43. Период затухающих колебаний T = 4с; логарифмический декремент затухания N = 1.6; начальная фаза φ = 0. При t=T/4 смещение точки x = 4,5 см. Написать уравнение движения

этого колебания. Построить график этого колебания в пределах двух периодов.

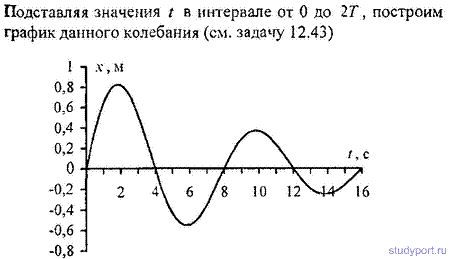
12.44. Построить график затухающего колебания, данного

уравнением x=5e -0,1t sinP/4t м.

12.45. Уравнение затухающих колебаний дано в виде x=5e -0,25t sinP/2tм. Найти скорость v колеблющейся точки в моменты времени t, равные: 0, T, 2T, 3Т и 4T,

12.46. Логарифмический декремент затухания математического маятника N = 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?

12.47. Найти логарифмический декремент затухания математического маятника, если за время t = 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l= 1м.

12.48. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: а) N = 0,01; б) N = 1.

12.49. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания N = 0,2 . Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?

12.50. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t = 3 мин?

12.51. Математический маятник длиной l = 0,5м, выведенный из положения равновесия, отклонился при первом колебании на х₁ = 5 см, а при втором ( в ту же сторону) — на x₂ = 4см. Найти время релаксации t, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е — основание натуральных логарифмов.

12.52. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на dl = 9,8см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания δ, чтобы: а) колебания прекратились через время t = 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращается в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был равным N = 6 ?

12.53. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой A_max = 7см, начальной фазой φ = о и коэффициентом затухания δ = 1,6 см -1 . На это тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид х = 5sin(10Pt-3P/4) см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.

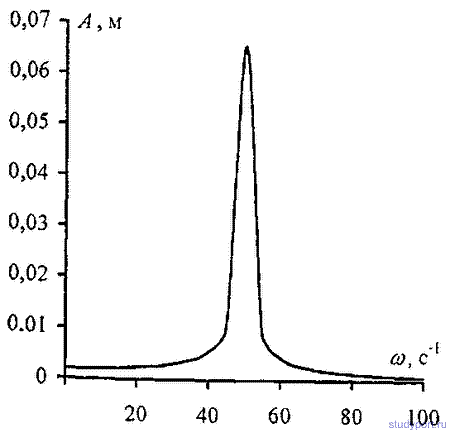
12.54. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания δ= 0,75 см -1 . Жесткость пружины k = 0,5кН/м. Начертить зависимость амплитуды А вынужденных колебаний гирьки от частоты внешней периодической силы, если известно, что максимальное значение внешней силы F₀ = 0,98 Н. Для построения .трафика найти значение А для частот: w= 0, w= 0,5, w = 0,75, w = w₀, w = w=1,5w₀ и w = 2w₀, где w₀— частота собственных колебаний подвешенной гири.

12.55. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на x₀ = 2 см под действием груза массой m₀ = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M= 10 кг.

12.56. Найти длину волны λ колебания, период которого T = 10 -14 с. Скорость распространения колебаний с = 3 * 10 8 м с.

12.57. Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду A =0.25 мм. распространяются в воздухе. Длина волны λ = 70 см. Найти скорость с распространения колебаний и максимальную скорость V_max частиц воздуха.

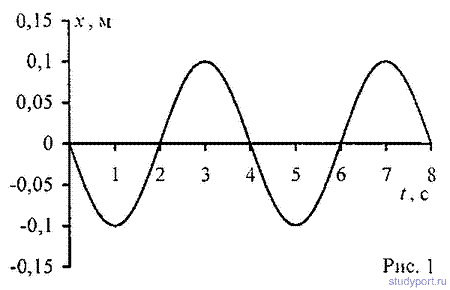
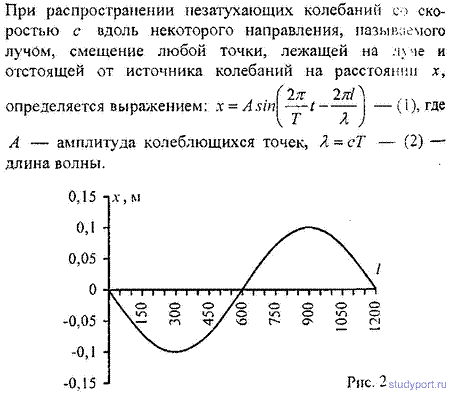
12.58. Уравнение незатухающих колебаний имеет вид

x=10sinP/2*t см. Найти уравнение волны, если скорость распространения колебаний с = 300м*с. Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии

l = 600 м от источника колебаний. Написать и изобразить графически уравнение колебания для точек волны в момент времени t= 4 с после начала колебаний.

12.59. Уравнение незатухающих колебаний имеет вид x = 4sin600Pt см. Найти смещение x от положения равновесия

точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01 с после начала колебаний. Скорость распространения колебаний с = 300 м/с.

12.60. Уравнение незатухающих колебаний имеет вид x=sin2,5Pt см. Найти смещение х от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии

l = 20м от источника колебаний, для момента времени t = 1с после начала колебаний. Скорость распространения колебаний с = 100 м*с.