Функции plot3d2 и plot3d3 являются аналогами функции plot3d, поэтому
имеют такой же синтаксис:
plot3d2(x,y,z,[theta,alpha,leg,flag,ebox]Построить график заданный системой уравнений при помощи функции plot3d2),
plot3d3(x,y,z,[theta,alpha,leg,flag,ebox]Построить график заданный системой уравнений при помощи функции plot3d2)
Эти функции предназначены для построения поверхности, которая задается набором граней. Т. е. если функция plot3d по входным данным сможет построить лишь отдельно стоящие друг от друга плоские грани, то plot3d2 (plot3d3) проинтерпретирует взаимное расположение этих граней в виде цельного геометрического тела.
Отличие функций plot3d2 и plot3d3 сходно с различием действия функций plot3d и plot3d1, а также surf и mesh. Plot3d2 строит поверхность, при этом выводит сетку и заливает все ячейки одним из цветов, по умолчанию синим. Plot3d также выводит сетку, однако оставляет все ячейки без заливки (т. е. белыми)
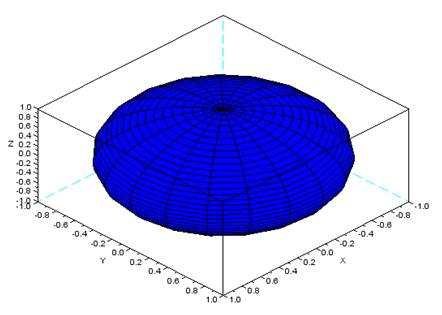
Пример 8. Построить сферу 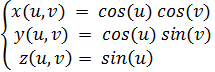
При построении графиков поверхностей, заданных параметрически 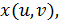
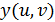
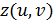
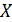
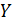
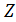
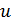
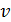
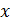
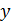
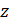
1. Если 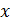
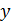
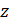
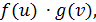
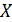
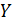
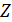
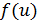
2. Если 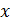
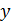
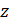
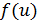
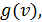
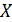
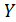
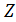
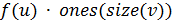
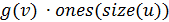
Отметим также, что здесь linspace-функция, возвращающая массив с линейным приращением значений в заданном диапазоне.
Например, u=linspace(-%pi/2,%pi/2,40) значит, что параметр 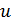
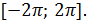
Построение сферы с помощью функции plot3d2
Теперь посмотрим, как эту же задачу выполнит функция plot3d.
График сферы, построенный функцией plot3d2
Пример 9. Построить сферу 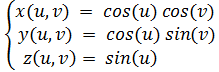
Определим параметры 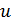
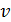
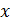
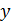
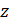
u=linspace(-%pi/2,%pi/2,40);v=linspace(0,2*%pi,20);X=cos(u)’*cos(v);Y=cos(u)’*sin(v);Z=sin(u)’*ones(v);plot3d(X,Y,Z);
Проиллюстрируем действие функции plot3d3 на этом же примере.
Пример 10. Построить сферу 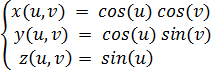
Определим диапазоны изменения параметров u и v, как и предыдущих примерах, лишь уменьшив количество значений для массива 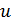
Вычислим значения функций 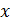
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Построить график заданный системой уравнений при помощи функции plot3d2
plot3d2 — plot surface defined by rectangular facets
Calling Sequence
Parameters
- X, Y, Z: 3 real matrices defining a data structure.
- vect : a real vector.
- : This represents a sequence of statements key1=value1, key2=value2. where key1, key2. can be one of the following: theta, alpha ,leg,flag,ebox (see definition below).
- theta, alpha : real values giving in degree the spherical coordinates of the observation point.
- leg : string defining the labels for each axis with @ as a field separator, for example «X@Y@Z».
- flag : a real vector of size three. flag=[mode,type,box].
- mode : an integer (surface color).
- mode>0 : the surface is painted with color "mode" ; the boundary of the facet is drawn with current line style and color.
- mode=0: a mesh of the surface is drawn.
- mode Description
plot3d2 plots a surface defined by rectangular facets. (X,Y,Z) are three matrices which describe a surface. The surface is composed of four sided polygons. The X-coordinates of a facet are given by X(i,j),X(i+1,j),X(i,j+1),X(i+1,j+1). And similarly Y and Z are Y and Z coordinates. The vect vector is used when multiple surfaces are coded in the same (X,Y,Z) matrices. vect(j) gives the line at which the coding of the jth surface begins. Like in plot3d , the same properties are editable (see surface_properties and axes_properties ).
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать
Как в maple построить три графика на одном
Видео:Как построить график функции без таблицыСкачать
Графические средства системы Maple.
Maple содержит функцию plot, для построения двумерных графиков (2D типа) и функцию plot3d (2D типа) для построения трехмерных графиков. Для обеспечения построения типовых графиков необходимо указать функцию, график которой строится и пределы изменения независимых переменных.
Построение двумерных графиков.
Для построения двумерных графиков служит функция plot(f, h, v)или plot(f, h, v, o),
где f– функция или функции для построения графика, h— переменная с указанием области ее изменения по горизонтали, v— заданная опционально переменная с указанием области изменения по вертикали, o— опция или набор опций, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.).
Самыми простыми формами задания этой функции служат:
plot(f, xmin..xmax) –построение графика функции f, заданной только именем;
plot(f(x), x=xmin.. xmax) –построение графика функции f(x).
Диапазон изменения независимой переменной задается как xmin..xmax,где xmin и xmax–минимальное и максимальное значения x, .. ( две точки) – составной символ, указывающий на изменение независимой переменной. Имя переменной x – условно. Возможны различные обозначения имени переменных.
Для двумерной графики возможны следующие опции:
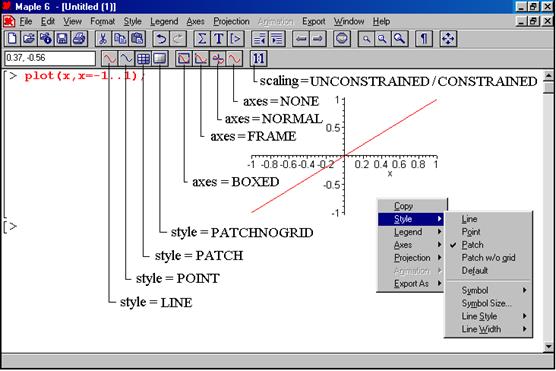
axes – вывод различного типа координат (axes=NORMAL – обычные оси, выводятся по умолчанию, axex=BOXES – график заключается в рамку с оцифрованными осями, axes=FRAME – оси в виде перекрещенных линий, axes=NONE – оси не выводятся;
color – задает цвет кривых: red -красный, green — зеленый, blue — синий, black — черный, white — белый, gold — золотистый, yellow -желтый, khaki — хаки и т.д. ;
coords – задание типа координатных систем. В частности, задание полярной системы координат производится при помощи опции coords=polar;
numpoints – задает минимальное количество точек графика ( по умолчанию numpoints=49);
scaling — задает масштаб графикаCONSTRAINED (сжатый) или UNCONSTRAINED (несжатый) по умолчанию;
size – задает размер шрифта в пунктах;
style — задает стиль построения графика (POINT — точечный, LINE – линиями);
symbol – задает вид символа для точек графика: BOX — mпрямоугольник, CROSS _ крест, CIRCLE — окружность, POINT — точка, DIAMOND — ромб;
title — задает построение заголовка графика (title=”string”, где string – строка);
trickness – определяет толщину линий графиков (0,1,2,3, по умолчанию 0);
view -=[A, B] – определяет мимнимальные и максимальные координаты, в пределах которых график будет отображаться на экране,
A =[xmin..xmax], B=[ymin..ymax] ( по умолчанию отображается вся кривая);
xtickmarks — задает минимальное число отметок по оси X;
ytickmarks — задает минимальное число отметок по оси Y.
Пример 1.Построить графики функций, заданных в декартовойсистеме координат .
1) Построение параболы.
2) Построение графиков двух функций в одной системе координат.
Рис. 2. Графики двух функций
Пример 2.Построить график функции, заданной параметрически
Указание. Используйте функцию plot в следующей форме:
plot([f1(t),f2(t),t=tmin..tmax],h,v,o), гдегде f– функция или функции для построения графика, h— переменная с указанием области ее изменения по горизонтали, v— заданная опционально переменная с указанием области изменения по вертикали, o— опция или набор опций, задающих стиль построения графика. Если функции f1(t),f2(t) содержат периодические функции, например, тригонометрические, то для получения замкнутых линий, дипазон изменения t задается обычно 0..2*Pi или –Pi..Pi.
Задание указателей масштаба h и v необязательно, но их целенаправленное использование позволяет получить вид графика, удовлетворяющий всем требованиям пользователя.
Построение графика циклоиды, заданной параметрически.
Рис. 3. Циклоида
Пример 3. Построить линии, заданные уравнениями в полярных координатах
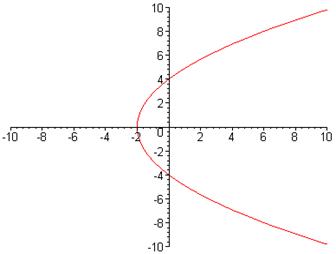
1) Построение параболы.
Рис. 4. Парабола , заданная в полярных координатах
2) Построение кардиоиды.
3) Построение трехлепестковой розы.
Рис.6. Трехлепестковая роза
Пример 3. Построить графики функций, заданных неявно
Указание. Для построения графиков неявных функций используется пакет plots, содержащий около 50 различных функций, среди которых находится функция implicitplot, служащая для построения графиков неявных функций.
1) Построение эллипса.
2) Построение гиперболы.
3) Построение линии
Рис.9. Часть окружности
Построение графиков поверхностей.
Для построения графиков трехмерной поверхности Maple имеет встроенную в ядро функцию plot3d или при помощи пакета plots, содержащего функцию implicitplot3d, предназначенную для построения графиков неявных функций.
plot3d(expr1,x=a..b,y=c..b,p);
plot3d(f,x=a..b,y=c..b,p);
plot3d([exprf, exprh, exprg], s=a..b,t=c..b,p);
plot3d([f,g,h], a..b,c..b,p)
В первых двух формах plot3d применяется для построения обычного графика одной поверхности, в других формах – для построения графика с параметрической формой задания поверхности. В приведенных формах:
f, g, h – функции, выражение, отражающее зависимость от x и y, exprf, exprh, exprg — выражения, задающие поверхность параметрически, s, t, a, b — числовые константы действительного типа, c, d -числовые константы или выражения действительного типа, x, y, s, t — имена независимых переменных, p — параметры-опции, которые задаются аналогично их заданию для функции plot.
Параметры функции plot3d.
axes= —задает вид координатных осей (NORMAL, BOXED, FRAIM, NONE. По умолчанию NONE, без осей.);
lables=[x,y,z] – задает надписи по осям. По умолчанию строки пустые;
view=[xmin..xmax, ymin..ymax, zmin..zmax] или view=zmin..zmax – задает минимальные и максимальные координаты поверхности для ее видимых участков;
tickmarks=[1,n,m] – задает характер маркировки по осям x, y, z. Числа 1, n, m имеют значения не менее 1.
Видео:Полярный график в MathCAD 14 (13/34)Скачать
Методы решения математических задач в Maple
Данная книга является учебным пособием по дисциплинам "Математика и информатика", "Информационные технологии". Пособие представляет собой практическое руководство по изучению возможностей пакета аналитических вычислений Maple. Подробные теоретические сведения чередуются с практическими заданиями. Последовательное изучение тем и выполнение заданий позволит шаг за шагом освоить основные приемы работы в математической системе Maple. Учебное пособие предназначено для студентов 1 и 2 курсов социально-психологического и естественно-географического факультетов университета, а также для аспирантов и научных работников, использующих математические методы и модели в естественнонаучных исследованиях.
Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать
Лабораторная работа: Двумерная графика системы Maple
· уметь применять указанные команды для отображения результатов вычислений в виде графических образов.
Команда plot () – многофункциональная команда двумерной графики. Расположена она в системной библиотеке Maple, и поэтому доступна в любое время. Данная команда позволяет строить график одной или нескольких функций одной вещественной переменной, заданных в явном или параметрическом виде, а также отобразить множество точек в декартовой или полярной системе координат. Синтаксис команды: plot (f, h, v, опции);
Здесь f – функция, график которой необходимо отобразить, h – диапазон изменения независимой переменной по горизонтальной оси графика, v– диапазон изменения значения функции вдоль вертикальной оси графика.
Диапазон изменения независимой переменной h задается в виде x = а..b, где а и b– наименьшее и наибольшее значения изменения переменной, а х – имя независимой переменной. Если диапазон не задан (т.е., второй параметр представляет собой просто имя независимой переменной в функции), то по умолчанию принимается интервал ее изменения –10..10. Этот параметр (с диапазоном или нет) обязательно должен присутствовать при задании графика командой plot().
Вертикальный диапазон v ограничивает вывод графика определенной областью изменения функции. Он необязателен, как и опции, задающиеся в виде уравнений имя_опции=значение. При отсутствии явного задания опций принимаются их значения по умолчанию.
С помощью опций определяют вид отображаемого графика: толщину, цвет и тип линии графика, тип осей координат, размещение надписей и т.д. Задаются опции в форме уравнений имя_опции = значение. Набор возможных опций во всех командах двумерного графического вывода, за некоторым исключением, одинаков. В табл. 1 представлены все опции двумерной графики и соответствующие им значения(умалчиваемые значения подчеркнуты).
Таблица 1. Опции двумерной графики
Задает цвета кривых, отображаемых на график. В качестве значения этой опции может выступать одно из зарезервированных значений цвета в Maple: aquamarine, black, blue, navy, coral, cyan, brown, gold, green, gray, grey, khaki, magenta, maroon, orange, pink, plum, red, sienna, tan, turquoise, violet, wheat, white и yellow.
Можно определить и собственный цвет, соответствующий смешению заданных частей красного, зеленого и синего цветов. Это делается с помощью следующей командыmacro (palegreen=COLOR (RGB.5607.7372.5607)), где palegreen– имя константы нового цвета, в котором красный составляет 0.5607 части, зеленый 0,7372 и синий 0.5607, В дальнейшем это имя можно использовать для задания цвета аналогично именам встроенных цветов.
Ниже приводятся примеры работы с командой plot (). Первым примером будет отображение графика функции
на интервале [-4,4] изменения независимой переменной х с созданием надписи.
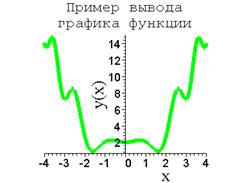
Пример 1. Отображение графика функции с надписью.
title=`Пример выводаnграфика функции`,
labelfont=[TIMES, ROMAN, 16]);
Для удобства восприятия в примере 1 (и в некоторых других нижеследующих примерах) команды набраны в столбик, каждая отдельно. На практике команды набираются в строку, одна за одной, без пробелов. Для создания многострочной надписи в строке значения опции title использован символ перехода на новую строку (n).
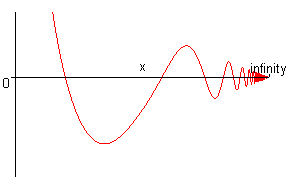
Команда plot () отображает графики функций не только на конечном интервале изменения независимой переменной, но и на бесконечном:
>plot (3*cos(x)/x, x=0..infinity, – 1.5..1, color=red, numpoints=1000, thickness=1);
Здесь пришлось ограничить область значений функции диапазоном [-1. 5,1], так как при х, стремящемся к нулю, функция стремится к бесконечности, а также задать больше точек на графике функции, иначе в районе надписи infinity не наблюдалась бы гладкость функции, а были бы явные сломы, которые не соответствуют поведению функции.
В явном виде можно представить не всякую функцию. Многие функции задаются в параметрической форме. Отображение графиков таких функций лишь немного отличается от вывода явно задаваемых функций. Отличие заключается в том, что параметрическая кривая задается в виде списка, где первый и второй элементы являются выражениями через параметр, соответственно, горизонтальной и вертикальной координат, а третий элемент списка задает изменение параметра в виде диапазона. Отображение параметрически заданной кривой показано на примере 2.
Пример 2. Отображение графика параметрически заданной функции.
При необходимости вывода нескольких функций на одном графике следует в команде plot () задавать функции в виде множества или списка, а значение опции color в виде списка позволяет задать цвет для вывода графиков функций. Если опция color не задана, то функции отображаются в соответствии со списком цветов по умолчанию.
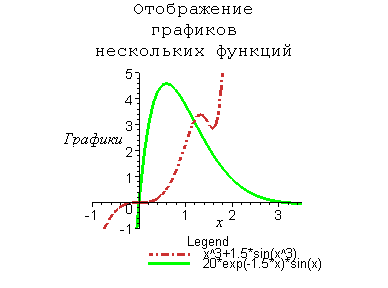
Пример 3. Отображение графиков нескольких функций.
legend=[«x^3+1.5*sin (x^3)», «20*exp (-1.5*x)*sin(x)»],
labelfont=[TIMES, ITALIC, 12]);
Рекомендуется при выводе нескольких графиков также отображать легенду заданием списка значений опции legend. Легенду можно всегда скрыть или снова отобразить с помощью команды Show Legend меню Legend .
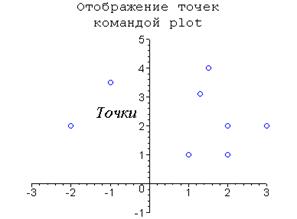
Команда plot () позволяет отображать на графике отдельные точки, которые задаются в виде списка списков, т.е. списка, элементами которого являются списки. Эти двухэлементные списки определяют координаты точек на плоскости. Для вывода точек необходимо задать значение опции style, равной POINT. Если этого не сделать, то Maple отобразит ломаную линию, соединяющую точки в последовательности их задания, не выделяя их специальными символами. В примере 4 точки, заданные своими координатами на плоскости, отображаются с использованием символа круг symbol = CIRCLE.
Пример 4. Отображение точек на плоскости.
labelfont=[TIMES, ITALIC, 16]);
2. Меню для работы с двумерной графикой.
После построения графика функции командой plot () или другой командой двумерной графики из пакета plots, его внешний вид можно изменить. Для этого надо переустановить значения некоторых опций с помощью команд основного меню интерфейса пользователя, контекстной панели инструментов или команд контекстного меню, отображаемого нажатием левой кнопки мыши при наведении указателя в область рисунка.
На рис. 1 показан общий вид интерфейса пользователя с меню и контекстной панелью инструментов для работы с графикой. Также на этом же рисунке отображено контекстное меню, появляющееся при щелчке правой кнопкой мыши, когда указатель расположен в области графического вывода. При выделении двумерной графики на рабочем листе меню Insert , Spreadsheet и Options , находящиеся в строке основного меню, заменяются новыми Style , Legend . Axes , Projection , Animation и Export , которые позволяют изменить основные опции построенного графика, а также сохранить его в различных форматах с помощью команд последнего меню. Все команды этих меню дублируются в контекстном меню, в котором дополнительно присутствует команда Сору копирования графики в Буфер обмена, а некоторая их часть в контекстной панели инструментов для двумерной графики. На рис. 1 показаны опции, которым соответствуют кнопки контекстной панели инструментов. Дополнительно к изменению основных меню сокращается список команд меню Format . Так меняется окно интерфейса пользователя при выделении двумерного графика на рабочем листе.
Команды Line (Линия). Point (Точка), Patch (Заливка) и Patch w / o grid (Заливка без сетки) меню Style устанавливают значение опции style, равной, соответственно, line, point, patch или PATCHNOGRID. На контекстной панели инструментов этим командам соответствуют первые четыре кнопки (рис. 1).
Рис. 1. Интерфейс пользователя при выделении графики
Подменю Symbol (Символ), Line Style (Тип линии) и Line Width (Толщина линии) позволяют установить значения опций symbol, linestyle и thickness, а команда Symbol Size отвечает за установку и изменение размеров символов отображения точек при отображении линий точками, т.е. когда установлена опция linestyle=POINT. Кнопок на контекстной панели инструментов для этих опций не предусмотрено.
Команда Show Legend меню Legend добавляет или удаляет легенду из выделенного графика. Она работает как переключатель: если легенда помещена на график, то слева от команды отображается «галочка», если на графике легенда отсутствует, то отсутствует и «галочка». Команда Edit Legend отображает диалоговое окно Legend Labels , в котором можно изменить надписи легенд для кривых, отображаемых на графике. Для этого следует в раскрывающемся списке Curve выбрать необходимую кривую, а в поле Label ввести новое значение надписи.
Команды меню Axes (Оси) позволяют установить значения BOXED, FRAME, NORMAL и NONE опции axes. На контекстной панели инструментов им соответствуют четыре кнопки, показанные на рис. 1.
Меню Projection (Проекция) устанавливает значения опции scaling. На панели инструментов значения этой опции можно устанавливать с помощью последней кнопки. Если она не нажата, то соответствует значению unconstrained, если нажата – установлено значение constrained.
Меню Animation специально предназначено для анимации изображений и становится доступным, когда в документе Maple графика выводится командой создания анимации animate ().
Командами последнего меню Export можно сохранить выделенный на рабочем листе график в одном из следующих форматов: EPS, GIF, JPG, BMP и WMF.
Все перечисленные команды меню можно выполнить из контекстного меню, в котором кроме этих команд присутствует команда Сору (Копировать), копирующая графический рисунок в Буфер обмена операционной системы Windows для вставки его в документ другого приложения или обработки какой-либо графической программой. Отметим, что скопировать график в Буфер обмена можно и командой Сору меню Edit .
1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. – М.: Мир, 1997. – 208 с.
2. Дьяконов В.П. Математическая система MapleV. – М.: Издательство «Солон», 1998.
3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.
4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.:БХВ – Петербург, 2001. – 528 с.
5. Манзон Б.М. MapleVPowerEdition – М.: Информационно-издательский дом «Филинъ», 1998 г.
📽️ Видео
Математический анализ, 16 урок, Исследование функции и построение графикаСкачать
Основы работы в Mathcad ГрафикиСкачать
ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Как построить график линейной функции.Скачать
Построение кривой в полярной системе координатСкачать
MathCAD Построение графика быстрым способомСкачать
Математический анализ. ДКР, задание 2. Построение графика функции, заданной параметрическиСкачать
Построение графика параметрически заданной функцииСкачать
ГРАФИК ФУНКЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
Построение графиков с помощью производныхСкачать
Построение графика квадратичной функцииСкачать
Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать
Построение графика функции в полярных координатахСкачать
Как строить графики без таблицСкачать
- mode : an integer (surface color).











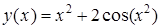 на интервале [-4,4] изменения независимой переменной х с созданием надписи.
на интервале [-4,4] изменения независимой переменной х с созданием надписи.