Построение уравнений регрессии в программе статистика (6 видео)

ГЛАВА 16 Примеры анализа данных в системе STATISTICA

В этой главе мы рассмотрим несколько примеров анализа данных с помощью системы STATISTICA. Первый пример относится к области маркетинга (мы показываем возможности модуля Множественная регрессия), три следующие примера к промышленным приложениям (мы показываем возможности модулей Планирование эксперимента и Карты контроля качества), пятый пример иллюстрирует возможности STATISTICA по наложению результатов анализа на географические карты.

Еще раз отметим, что современная STATISTICA — это средство разработки приложений в конкретных областях (бизнесе, медицине, промышленности и др.). Библиотека STATISTICA содержит более 10 000 тщательно отлаженных и проверенных на практике процедур анализа данных. Развитие системы естественно приводит к созданию средств разработки собственного интерфейса и использования библиотеки STATISTICA для создания оригинальных модулей, включающих, наряду с процедурами STATISTICA, алгоритмы разработчика. Все эти процедуры объединяются общим интерфейсом, средствами управления данными и графикой STATISTICA.

Именно в создании средств для разработки приложений мы видим будущее систем анализа данных.

Пример основан на реальных данных, описывающих рынок пива в Греции (см. статью Kioulofas К. Е. «An Application of Multiple Regression Analysis to the Greek Beer Market» в журнале «Journal of Operational Research Society», Vol. 36, № 8, p. 689-696,1985).

Известно, что этот рынок поделен между 5 фирмами, обозначенными далее А, В, С, D и Е. До 1981 года на рынке присутствовали фирмы А, В и С, в 1981 году на рынок пришли фирмы D и Е. Но уже в’ 1983 году фирма D не выдержала конкуренции, а у фирмы А возникли финансовые проблемы.

В следующей таблице представлены объемы продаж в отрасли и доля каждой фирмы.

Можно заметить, что после появления фирм D и Е произошло резкое снижение доли фирмы А. Две новые фирмы D и Е по-разному освоили рынок. Фирма D имела большие производительные способности, чем фирма Е, но заметно отстала по объемам продаж. Этот пример интересен тем, что показывает соотношение затрат на рекламу и производство.

Будем считать, что основным показателем эффективности рекламы является объем продаж фирмы. В этой таблице представлены расходы на рекламу каждой фирмы и ее доля в рекламе.

Понятно, что вхождение в отрасль фирм D и Е потребовало больше расходов на рекламу (в процентном отношении к объему продаж). Это отчетливо видно из следующей таблицы:

Заметим, фирма D в 1982 году резко снизила расходы на рекламу, что, возможно, стало причиной потери рынка.

Предполагается, что для рекламы используются следующие средства массовой информации: телевидение, газеты, журналы и радио.

Эффективность рекламы в каждом случае различна, и возникает вопрос о количественных зависимостях между объемом продаж и расходами на рекламу в каждом из средств массовой информации. Обычно доля телевидения составляет 70-90%, и поэтому в таблице, представляющей распределение расходов на рекламу между средствами массовой информации, все СМИ, кроме телевидения, объединены в одну группу «другие».

На реальный объем продаж пива влияют также такие факторы, как температура воздуха, число туристов и индекс потребительских цен (инфляция).

В предлагаемой модели теоретическая зависимость основывается на предположении, что объем продаж за период t (далее это месяцы) является функцией объема продаж за прошлый период расходов на рекламу в периоды t и t-1, количества туристов, значений температуры и индекса розничных цен.

S_t — объем продаж (в драхмах);

A_t — ассигнования на рекламу;

T_t — число туристов в месяц t;

W_t — средняя температура воздуха;

P_t — индекс розничных цен.

Итак, мы построили модель зависимости, но коэффициенты этой модели неизвестны. Эти коэффициенты оцениваются из исходных данных в модуле Множественная регрессия.

Оценка коэффициентов по методу наименьших квадратов выявила статистическую незначимость переменных W_t и P_t, и они были исключены из дальнейшего анализа.

В результате получилось уравнение, содержащее меньшее число переменных:

Оценим коэффициенты этого уравнения, используя реальные данные. Для анализа использовались данные о месячных продажах за 2 года. Число наблюдений равнялось 24. Результаты регрессии приведены в таблице:

Значения коэффициента детерминации R 2 , близкие к единице, говорят о хорошем приближении линии регрессии к наблюдаемым данным и о возможности построения качественного прогноза.

Низкое значение коэффициента детерминации R 2 для фирмы D объясняется низкой эффективностью рекламной кампании и трудностями на административном уровне. Можно сделать вывод, что модель плохо применима к фирме D.

Статистики Дарбина—Уотсона свидетельствуют об отсутствии автокорреляции остатков при 5%-м уровне значимости, т. к. все ее значения по модулю меньше 1,96.

Все значения регрессионных коэффициентов значимы при уровне значимости 0,5, за исключением коэффициентов при A_t для фирм В, D и Е.

Одним из возможных объяснений этого факта является то, что показатели этих фирм зависят от рекламной деятельности за прошлый период времени, то есть от А_t-1

Это подтверждается тем, что для этих фирм коэффициенты при A_t-1 значимы на уровне 95%. Более того, можно заметить, что показатели всех фирм, кроме фирмы Е, имеют положительную корреляцию с числом туристов. Незначительную корреляцию между туризмом и объемами продаж фирмы Е можно объяснить недавним появлением этой фирмы. Объемы продаж всех фирм также находятся под влиянием объемов продаж в прошлом периоде, S_t-1 возможно, благодаря эффекту «привычки» потребителей к торговым маркам. Значимость этого параметра с распределенным лагом также наводит на мысль о некоторых обучающих эффектах.

Продажи фирмы А имеют значительную положительную корреляцию с ее расходами на рекламу за период t, что отличает ее от других фирм. Окончательно взаимосвязь между рыночными продажами и совокупными расходами на рекламу положительна и значима при уровне 5%.

Представленные выше результаты регрессии образуют основу оценки эффективности совокупных расходов на рекламу.

Покажем, как строятся такие модели в системе STATISTICA. Для этих целей обычно используется модуль Множественная регрессия.

В этом модуле собраны методы, позволяющие оценить зависимость одной переменной от нескольких других переменных.

Переменная, для которой строится зависимость, называется зависимой (по-английски dependent variable). Эта переменная входит в левую часть уравнения, описывающего зависимость (см. уравнение (*)). Переменные, от которых мы хотим построить зависимость, называются независимыми переменными (по-английски independent variables) или предикторами (от английского predict — предсказывать). Эта переменная входит в правую часть уравнения, описывающего зависимость. Сам термин множественная регрессия (по-английски multiple regression) означает, что модель может содержать несколько предикторов, позволяющих предсказывать зависимую переменную.

Итак, общая идея состоит в том, чтобы по значениям предикторов предсказывать значения зависимой переменной, например, по значениям продаж и расходам на рекламу в текущем и предыдущем месяце предсказывать продажи в следующем месяце.

Конечно, количество предикторов можно увеличить, например, ввести объем продаж у конкурентов или какие-то другие, имеющие смысл и доступные наблюдению переменные. Однако здесь имеется тонкость, предикторы могут оказаться зависимыми между собой.

Переменные, которые следует включить в модель, определяет специалист в предметной области. Затем нужно выполнить следующие действия.

Шаг 1. Запустите модуль Множественная регрессия.

Шаг 2. Введите исходные данные в файл системы STATISTICA. Назовите его, например, Beer.sta.

Шаг 3. Определите переменные в модели. Задайте S в качестве зависимой переменной и S1. P — в качестве независимых переменных, или предикторов. После этого стартовая панель модуля будет выглядеть так:

Шаг 4. Нажмите кнопку ОК. Появится диалоговое окно результатов, в котором отображаются итоги стандартной процедуры.

Измените процедуру на Пошаговую с включением. Для этого нажмите на кнопку Отмена и в появившемся диалоговом окне Определение модели выберите в поле Процедура опцию Пошаговая с включением. В этой процедуре система начинает построение модели с одного предиктора, затем, используя F-критерий, в модель включается еще один предиктор и т. д. На каждом шаге вычисляется коэффициент множественной корреляции. Квадрат коэффициента множественной корреляции, коэффициент детерминации, свидетельствует о качестве построенной модели. Нажмите кнопку ОК.

В появившемся окнеПошаговая множественная регрессия снова нажмите ОК.

Теперь перед вами диалоговое окно результатов, полученных с помощью пошаговой процедуры с включением. Следует отметить, что в нем указаны стандартизованные коэффициенты регрессии.

Заметим, если вы предполагаете, что в модели должно присутствовать небольшое число предикторов, то естественно использовать пошаговый метод с включением предикторов. Если вы предполагаете, что в модели должно присутствовать большое число предикторов, то естественно использовать метод с исключением.

Шаг 5. Нажмите кнопку Итоговая таблица регрессии. Появится таблица результатов с подробными статистиками.

В столбце БЕТА показаны стандартизованные коэффициенты регрессии, а в столбце В — нестандартизованные коэффициенты. Все коэффициенты в таблице значимы, так как р-значения для каждого из них меньше заданной величины 0»05.

Шаг 6. В окне результатов нажмите кнопку Анализ остатков.

Шаг 7. В диалоговом окне Анализ остатков нажмите кнопку Статистика Дарбина—Уотсона. Эта статистика позволяет исследовать зависимость между остатками. Формально остатки представляют собой разность: наблюдаемые значения зависимой переменной минус оцененные с помощью модели значения зависимой переменной.

Зачем проверять зависимость остатков? Идея проста: если остатки существенно коррелированны (зависимы), то модель неадекватна (нарушено важное предположение о независимости ошибок в регрессионной модели).

Рассмотрим более подробно статистику Дарбина—Уотсона. Мы уделяем этой статистике так много внимания, потому что статистика Дарбина—Уотсона является стандартом для проверки некоторых видов зависимости остатков и с ней нужно научиться работать.

Статистика Дарбина—Уотсона используется для проверки гипотезы о том, что остатки построенной регрессионной модели некоррелированы (корреляции равны нулю), против альтернативы: остатки связаны авторегрессионной зависимостью вида:

где d_i независимые случайные величины, имеющие нормальное распределение с параметрами (0, s), i = 1 . n».

Формально статистика Дарбина—Уотсона вычисляется следующим образом:

Иными словами, сумма квадратов первых разностей остатков нормируется суммой квадратов остатков. Проведя вычисления, вы легко выразите статистику Дарбина—Уотсона через коэффициент корреляции: d = 2(1 — р).

Критические точки статистики Дарбина—Уотсона табулированы (см. например, Драйпер Н., Смит Г. Прикладной регрессионный анализ. М.: Финансы и статистика, т. 1. с. 211, см. также таблицу, показанную ниже).

В таблице приведены два критических значения статистики Дарбина—Уотсо-на: DL_k и DU_k — нижнее и верхнее, зависящие как от числа наблюдений, по которым оцениваются параметры, так и от числа предикторов k, которые включены в модель.

На графике видно, как меняются значения DL_k и DU_k в зависимости от числа наблюдений (k = 1, 2, 3, 4, 5).

Число наблюдений, для которого рассчитаны критические значения, указано в заголовках строк приведенной таблицы.

Итак, вы находите строку с нужным числом наблюдений и два смежных столбца с нужным числом предикторов. На пересечении строки и столбцов располагаются нижние и верхние критические точки статистики Дарбина—Уотсона.

Если нужно проверить гипотезу: «остатки независимы, то есть р =0», против общей альтернативы р не равно 0, поступают следующим образом. Вычисляют значение статистики Дарбина—Уотсона d. Для данного числа наблюдений и числа предикторов находят критические точки DL_k и DU_k в таблице, составленной для определенного уровня а. В приведенной таблице уровень a=0,05

Если d DU_k и 4 — d > DU_k, то гипотеза о независимости остатков не отвергается на уровне 2a.

Если нужно проверить гипотезу: «остатки независимы р = 0», против альтернативы р > 0, то есть остатки положительно автокоррелированы, поступают следующим образом. Вычисляют значение статистики Дарбина—Уотсона d. Находят по таблице критические точки DL_k и DU_k, вычисленные для определенного уровня a. Заметьте, в приведенной таблице a=0,05.

Если d DU_k, то гипотеза о независимости не отвергается на уровне a.

После того как мы познакомились со статистикой Дарбина—Уотсона, продолжим работу в модуле Множественная регрессия.

Шаг 8. Нажмите кнопку Предсказанные и наблюдаемые.

Шаг 9. Вернитесь в окно Результаты множественной регрессии и нажмите кнопку Предсказать зависимую переменную. Далее в полях А1 и S1 укажите значения текущего месяца, а в полях Т и А — значения на следующий месяц.

Нажмите кнопку ОК. Появится таблица результатов предсказания. На рисунке выделена ячейка, содержащая прогнозируемый объем продаж на следующий месяц.

Этот пример относится к промышленной статистике (см. Cornell J. А. (1990). How to Apply Response Surface Methodology, vol. 8 in Basic References in Quality Control: Statistical Techniques, edited by S. S. Shapiro and E. Mykytka. Milwaukee: American Society for Quality Control).

Любая машина или станок, используемые на производстве, позволяют операторам производить настройки, чтобы воздействовать на качество производимого продукта. Изменяя настройки, инженер стремится добиться максимального эффекта, а также выяснить, какие факторы играют наиболее важную роль в улучшении качества продукции.

В системе STATISTICA имеется мощный модуль планирования экспериментов, позволяющий эффективно планировать и анализировать эксперименты.

Задача состояла в том, чтобы исследовать факторы, влияющие на качество производимых пластиковых дисков.

Известно, что наибольшее влияние на качество оказывают следующие два фактора:

1) материал, характеризующийся отношением наполнителя к эпоксидной резине,

2) расположение диска в форме.

В качестве зависимой переменной рассматривалась плотность полученного диска.

Сначала использовался дробный факторный план 2 2 для того, чтобы определить адекватность модели первого порядка. В этой модели оба фактора комбинировались друг с другом на верхних и нижних значениях (всего имеется 4 комбинации). Но оказалось, что модель оказалась адекватной лишь для некоторой области значений факторов и неадекватной для всей значений факторов. На самом деле зависимость между факторами и откликом была нелинейной. Поэтому было решено использовать центральный композиционный план и применить модель второго порядка.

Центральный композиционный план может состоять из куба и звезды. Куб соответствует полному факторному плану — точки эксперимента располагаются в вершинах куба (фактически это факторный план 22).

Звезда содержит дополнительное множество точек, расположенных на одинаковых расстояниях от центра куба на отрезках, исходящих из центра и проходящих через каждую сторону куба.

В данном исследовании применялся ротатабельный план, в котором дисперсия отклика является постоянной во всех точках, одинаково удаленных от центра плана.

Пусть фактор А — это характеристика материала, из которого изготовлен диск, более точно, так называемое композиционное отношение (disk composition ratio), фактор В — положение диска в форме (position of disk in mold). Зависимая переменная, или отклик эксперимента, — плотность диска (Thickness).

Запустите модуль Планирование эксперимента.

На стартовой панели выберите Центральные композиционные планы, поверхности отклика и нажмите кнопку ОК.

В появившемся диалоговом окне выберите опцию Построение плана, а в поле Факторы/блоки/опыты — строку 2/1/10. Нажмите кнопку ОК.

Появится диалоговое окно План эксперимента для поверхности отклика. Нажмите на кнопку Имена факторов, значения и заполните таблицу в диалоговом окнеИтоги для переменных .

Нажмите кнопку Далее и выберите опции для настройки .отображения плана так, как показано на следующем рисунке. Сделайте точно все показанные настройки, чтобы получить нужный результат!

Просмотрите план. Для этого нажмите Просмотр/Правка/Сохранение.

Задание имени и сохранение экспериментального плана

Выберите Сохранить как файл данных. ; появится соответствующее диалоговое окно. Задайте имя плана disk.sta и нажмите кнопку ОК.

Вернитесь в диалоговое окно План эксперимента для поверхности отклика.

Нажмите кнопку Печать итогов. В зависимости от настроек вывода в диалоговом окне Параметры страницы/вывода результаты плана будут распечатаны на принтере или выведены в отчет.

В построенной таблице показан порядок сбора экспериментальных данных.

Данные, полученные в результате эксперимента, занесены в таблицу.

Содержание

Примерф решения эконометрических задач в Statistica
Задача 1. Построение и анализ линейной множественной регре с сии
Пошаговая регрессия в STATISTICA
📺 Видео

Видео:Множественная линейная регрессия в StatisticaСкачать

Примерф решения эконометрических задач в Statistica

Ниже приведено условия задач и текстовая часть решения. Закачка полного решения, в архиве rar, начнется автоматически через 10 секунд.

Видео:Эконометрика. Линейная парная регрессияСкачать

Задача 1. Построение и анализ линейной множественной регре с сии

В таблице 1.1. приведены ежегодные данные о совокупных личных расходах ; располагаемых личных доходах ; расходах на табак для США на период с 1959 по 1983 годы. Оцените множественную регрессию между регрессандом (эндогенной пер е менной) Var 1 и регрессорами (экзогенными пер е менными) Var 2, Var 3 и Var 4 используя данные за 25 лет. Дайте интерпретацию коэффициентам ре г рессии. Исследуйте степень корреляционной зависимости между переменными. Проверьте остатки на н а личие автокорреляции и гетероскедастичность.

Ежегодные данные о потребительских расходах и

располагаемых личных д о ходах для США на период с 1959 по 1983 годы

Используем пакет Statistica 6.0, модуль Множественная регрессия .

Создадим новый документ с данными, введем число переменных – 4 и число регис т ров – 25. Введем наименования переменных и исходные данные.

Вызовем модуль Множественная регрессия . (Команда Статист и ка  Множественная регрессия). Выберем переменные (кнопка ( Variables ). Зависимая ( Dependent ) – Var 1 ; независ и мые ( Independent ) – Var 2 , Var 3 , Var 4 .

Нажмем кнопку ОК в правом углу стартовой панели.

Появится окно результатов множественной регрессии.

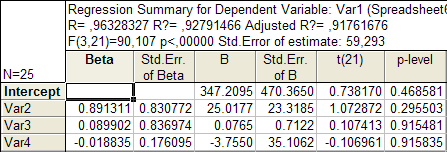
Результаты множественной регрессии в численном виде представлены в табл. 1.2.

В первом столбце таблицы 1.2 . даны значения коэффициентов beta — стандартизованные коэффициенты регрессионно го урав нения , во втором — стандартные ошибки beta , в третьем – В – точечные оценки пар а метров модели.

Далее, стандартные ошибки для коэффициентов модели В, значения ст а тис тик t-критерия и т.д.

Из таблицы 1.2 . мы видим, что оцененная модель имеет вид:

Var 1 = 347,2 + 25,018∙ Var 2 – 0,0765∙ Var 3 – 3 ,755 ∙ Var 4 (1.1)

TPE = 347,2 + 25,018 ∙ TIME – 0,0 765 ∙ PI – 3,755 ∙ TOB (1.2)

( t ) ( 0,738 ) (1, 073 ) ( 0,1074) (-0,107 )

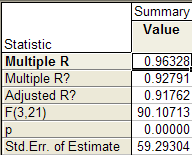
В верхней части таблицы 1.2 . и в таблице 1.3 . (а также в информационном окне) прив е дены следующие данные:

Коэффициент множественно й корреляции Multiple R = 0, 9633 ;

Коэффициент детерминации R-square = 0, 9279 ;

Скорректированный на поте рю степеней свободы коэффициент множественной д е термина ции Adjusted R 2 = 0, 9 176 ;

Критерий Фишера F = 90,107 ;

Уровень значимости модели р

Стандартная ошибка оценки Std. Error of estimate = 59,293 .

Проанализируем данные множественной регрессии.

Табличное значение критерия Стьюдента, соответствующее доверител ь ной вероятности  = 0,95 и числу степеней свободы v = n – m – 1 = 21 ; t кр. = t 0,025;21 = 2,080.

Сравнивая расчетную t -статистику коэффициентов уравнения с табличным значением, заключаем, что все полученные коэффициенты стат и стически не значимы.

Уравнение (1.2 . ) выражает зависимость совокупных личных расходов ( TPE ) от времени ( TIME ), личного дохода ( PI ) и расходов на табак ( TOB ). Коэффициенты уравнения пок а зывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В нашем случае совокупные личные расходы увеличиваются на 25,017 ден. ед. при увеличении времени на 1 ед. при неизменности показателей личного дохода и расходов на табак ; совокупные личные расходы увеличиваются на 0,0765 ден. ед. при увеличении показателя личного дохода на 1 ед. и неизменности показателей времени и расходов на табак ; совокупные личные расходы уменьшаются 3,755 ден. ед. при увеличении ра с ходов на табак на 1 ед. и неизменности показателей времени и личного дох о да.

Множественный коэффициент корреляции построенной модели (Multiple R) R = 0,9633 очень близок к единице, что говорит о высокой степени связи между исследуемыми факт о рами.

Коэффициент детерминации (R Square) R 2 = 0,9279, что говорит о том, что 92,79 % вари а ции переменной TPE объясняется вариацией переменных TIME , PI , TOB и только 7, 21 % приходятся на долю других неучтенных факторов.

Критическое (табличное) значение критерия Фишера для доверительной вероятн о сти  = 0,95 и числа степеней свободы v 1 = 25 – 3 = 22 и v 2 = 25 – 1 = 24: F кр . = F 0,05;22;24 = 2,01.

Расчетное значение критерия Фишера F = 90,107 намного превышает табличное значение критерия F табл. = 2,01, что говорит о хорошем качестве п о строенной модели (модель адекватна экспериментальным данным). Уровень значимости p = 0,00000 показывает, что построенная регрессия высоко знач и ма.

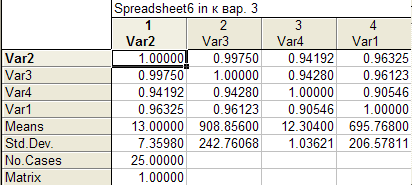
Исследуем степень корреляционной зависимости между переменными. Для этого п о строим корреляционную матрицу. Чтобы корреляционная матрица была построена при множественной регрессии, нужно установить флажок в строке Review descriptive statistics , correlations matrix в окне Multiple Regre s sions .

Корреляционная матрица приведена в таблице 1.4.

Из корреляционной матрицы следует, что на расходы на отдых все и с следуемые факторы оказывают значительное и примерно одинаковое влияние (коэффициенты корреляции между Var 1 и Var 2, Var 3, Var 4 равны соответственно 0,9 9975 ; 0,9 4192 ; 0, 96325 ). Из корреляционной матрицы также следует, что между факторами им е ется мультиколлинеарность (коэффициенты корр е ляции между регрессорами Var 2, Var 3, Var 4 также высоки и примерно одинаковы).

Проведем анализ остатков от регрессии.

Остатки представляю т собой разности между наблюдае мыми значениями и модел ь ными, то есть значениями, под считанными по модели с оцененными параметрами.

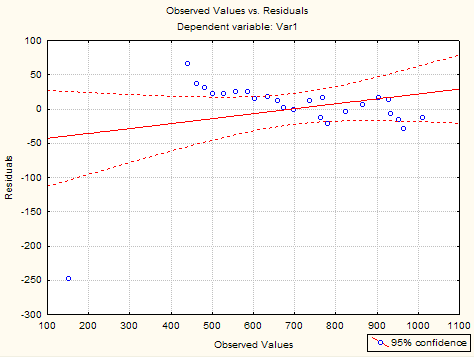
По кнопке Observed v s . residuals появится график (рис.1.1. ), который г о ворит о неслучайном р азбросе стандартных отклонений .

Рис. 1.1. Наблюдаемые переменные-остатки

Проверим остатки на наличие автокорреляции. Для этого вычислим ст а тистику Дарбина-Уотсона ( Darbin-Watson Stat ). Результаты вычисления статистики Дарбина-Уотсона привед е ны в табл. 1.5.

Из табл. 1.5 определяем наблюдаемое значение критерия Дарбина-Уотсона:

По таблице приложения 4 [1] определяем значащие точки d L и d U для 5% уровня зн а чимости.

Для m = 3 и n = 25 d L = 1,123; d U = 1,654.

Так как 4 — d U DW 4 — d L ( 2,346 2,469 ), то гипотезу об отсутствии автокорреляции мы не можем принять и не можем опровергнуть, так как значение статистики попало в зону неопределенности критерия .

Для проверки наличия гетероскедастичности воспользуемся тестом Па р ка. В Excel рассчитаем логарифмы значений e 2 , Var 2 , Var 3 и Var 4 (см. табл. 1.6).

Видео:Множественная регрессия в программе Statistica (Multiple regression)Скачать

Пошаговая регрессия в STATISTICA

Опубликовал: pvi777 в категорию Материалы по Dell StatSoft Statistica — Дата добавления: 17.02.2022, 22:37

Следующий пример основан на файле данных Job_prof. sta (взятом из работы Neter, Wassermanand Kutner, 1989, стр. 473). Этот файл данных можно открыть вызвав команду Открыть в меню Файл наиболее вероятно, что этот файл данных находится в директории /Examples/Datasets. Первые четыре переменные (Test1-Test4) представляют четыре различных теста на пригодность, направленных каждому из 25 претендентов, участвующих в конкурсе на замещение конторских должностей в компании. Все 25 претендентов были приняты на работу вне зависимости от набранных ими баллов по тестам. По истечении испытательного срока рабочие качества каждого из служащих были оценены, и показатель профессиональной пригодности был записан в качестве значений переменной (Job_prof).

Цель исследования. С использованием пошаговой регрессии мы проанализируем переменные (или подмножество переменных), позволяющие наиболее точно предсказать профессиональную пригодность претендента. Таким образом, зависимой переменной будет Job_prof, а переменныеTest1-Test4 играют роль независимых переменных.

Начало анализа. Выберите Множественная регрессия в меню Анализ. В появившемся диалоговом окне стартовой панели модуля Множественная регрессия нажмите кнопку Переменные и выберите переменную Job_prof в качестве зависимой переменной, а переменные Test1-Test4 в качестве независимых. После этого выберите опцию Гребневая регрессия и пошаговый анализ во вкладке Дополнительно. Далее нажмите кнопку OK для отображения диалогового окна Определение модели.

Определение модели для пошаговой регрессии. Вы можете выбрать следующие процедуры для проведения анализа данных: стандартная, пошаговая с включением и пошаговая с исключением. Наиболее часто используемой процедурой является процедура с пошаговым включением предикторов, которая осуществляет выбор предикторов на каждом шаге, добавляя или удаляя их из модели, исходя из заданного пользователем критерия (более подробную информацию см. в работеNeter, Wasserman and Kutner, 1989, а также в разделе Примечания и техническая информация). Поэтому мы используем пошаговую регрессию с включением предикторов для анализа данных нашего примера.

Во вкладке Быстрый диалогового окна Определение модели в поле Процедура выберите Пошаговая с включением. Далее во вкладке Пошаговый вы можете изменить значения F-включить иF-исключить. Однако, для проведения анализа в данном примере мы примем значения по умолчанию, равные 1 и 0, соответственно. Для просмотра результатов на каждом шаге анализа выберите опцию На каждом шаге в комбинированном окне Отображение результатов.

После этого, оставив все остальные установки без изменений, нажмите OK для запуска пошаговой регрессии с включением предикторов.

Шаг 0. Сначала на экран будет выведено диалоговое окно для модели, в которую не включена ни одна независимая переменная.

Шаг 1. Щелкните мышкой по кнопке Далее, чтобы приступить к следующему шагу анализа. На первом шаге производится раздельное оценивание каждой независимой переменной, и переменная, имеющая наибольшее значение F-критерия, которое к тому же больше или равно значения F- включить добавляется в уравнение регрессии.

Здесь переменная Test3 проходит значение F- включить (F>1. 0) и добавляется в модель. Во вкладке Дополнительно щелкните мышкой по кнопке Итоги по шагам для отображения таблицы результатов с итоговой информацией по выполненным шагам регрессионного анализа.

Щелкните на кнопке Далее диалогового окна Результаты множественной регрессии для выполнения следующего шага.

Шаг 2. Далее, на последующих шагах, при добавлении переменной в модель (исходя из значения F- включить), процедура пошаговой регрессии с включением предикторов будет исследовать переменные, включенные в модель, и, исходя из значения F-исключить, будет определять, следует ли удалить из модели какую-либо переменную. На этом шаге, переменная Test1 включается в модель. Щелчок мышкой по кнопке Итоги по шагам откроет следующее диалоговое окно с итоговыми результатами.

И снова, нажмите кнопку Далее в диалоговом окне Результаты множественной регрессии для перехода к шагу 3 в пошаговом анализе с включением предикторов.

Шаг 3 (Окончательное решение). Осталось две переменные, которые необходимо просчитать (Test2 и Test4). На этом шаге наибольшее значение F-критерия соответствует переменной Test4, поэтому, она добавляется в модель. При расчете переменной Test2, значение F-критерия оказалось меньше, чем значение F-включить, равное 1.0, следовательно, эта переменная не может быть включена в модель.

Таблица результатов Итоги по шагам теперь содержит результаты по всем переменным, которые были добавлены и оставлены в модели.

Тогда в соответствии с процедурой пошаговой регрессии с включением предикторов подмножество испытательных тестов (независимых переменных), которое наилучшим образом предсказывает оценки профессиональной пригодности (зависимую переменную), содержит тестыTest3, Test1, и Test4. Поэтому регрессионное уравнение будет следующим: