Построение уравнение тренда с помощью квадратичного уравнения (6 видео)

Вычисление трендов с помощью метода наименьших квадратов и прогнозирование

Среди компонентов временного ряда чаще других исследуется тренд. Именно тренд позволяет делать краткосрочные и долгосрочные прогнозы. Для выявления долговременной тенденции изменения временного ряда обычно строят график, на котором наблюдаемые данные (значения зависимой переменной) откладываются на вертикальной оси, а временные интервалы (значения независимой переменной) — на горизонтальной. В этом разделе мы опишем процедуру выявления линейного, квадратичного и экспоненциального тренда с помощью метода наименьших квадратов.

Модель линейного трендаявляется простейшей моделью, применяемой для прогнозирования: Y_i = β₀ + β₁X_i + ε_i. Уравнение линейного тренда:

Напомним, что метод линейного регрессионного анализа используется для вычисления выборочного наклона b₁ и сдвига b₀. Вычислив уравнение Ŷ_i = b₀ + b₁X_i, в него можно подставлять значения X, чтобы определять отклик Y.

Если при аппроксимации временного ряда с помощью метода наименьших квадратов первое наблюдение расположить в начале координат, поставив его в соответствие значению X = 0, интерпретация коэффициентов упрощается. Все последующие наблюдения получают целочисленные номера: 1, 2, 3, так что n-е (последнее) наблюдение будет иметь номер n – 1. Например, если временной ряд записывается на протяжении 20 лет, первый год обозначается цифрой 0, второй— цифрой 1, третий — цифрой 2 и так далее, а последний (20-й) год — числом 19.

В сценарии была упомянута компания Wm. Wrigley Jr. Company, являющаяся крупнейшим производителем жевательной резинки в США. Акции компании котируются на Нью-Йоркской фондовой бирже под аббревиатурой WWY. Рыночная стоимость компании составляет 13 млрд. долл. Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах приведены на рис. 7. Затем с помощью индекса потребительских цен (Consumer Price Index — CPI), вычисляемого Бюро статистики Министерства труда США, фактические доходы были преобразованы в реальные. Для этого следует умножить величину фактического дохода на коэффициент 100/CPI.

Рис. 7. Фактические и реальные доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах

Обозначим последовательные значения переменной X с помощью целых чисел от 0 до 19, а затем выполним регрессионный анализ с помощью Пакета анализа (рис. 8).

Рис. 8. Модель линейной регрессии для предсказания реального дохода компании Wm. Wrigley Jr.; построена с помощью Пакета анализа Excel

Уравнение линейной регрессии имеет следующий вид (см. ячейки Е17, Е18 на рис. 8): Ŷ_i = 498,656 + 45,485Х_i, где началом координат является 1982 год, а шаг переменной X равен одному году. Регрессионные коэффициенты интерпретируются следующим образом:

• Сдвиг b₀ = 498,656 представляет собой предсказанное среднее значение реальных доходов компании Wm. Wrigley Jr. Company в 1982 году.

• Наклон b₁ = 45,485 представляет собой предсказанное увеличение реальных доходов компании в среднем на 45,485 млрд. долл. в год.

Линия тренда и временной ряд реальных доходов показаны на рис. 9. График можно построить на основании уравнения линейной регрессии (колонка D; рис. 9а) или простым добавлением линии тренда на ранее построенный график доходов (рис. 9б). Видно, что на протяжении ряда лет доходы компании линейно возрастали. Скорректированный коэффициент r 2 равен 0,966 (ячейка Е6 на рис. 8). Следовательно, все изменения реальных доходов хорошо описываются линейным трендом. Возникает вопрос: а нельзя ли выбрать еще более точную модель? Для ответа на него рассмотрим еще две модели — квадратичную и экспоненциальную.

Рис. 9. Линия тренда реальных доходов компании Wm. Wrigley Jr., вычисленная с помощью метода наименьших квадратов, построенная: (а) на основании уравнения линейной регрессии; (б) добавлением линии тренда на график

Модель квадратичного тренда, или полиномиальная модель второй степени является простейшей нелинейной моделью, применяемой для прогнозирования: . Уравнение квадратичного тренда:

где b₀ – оценка сдвига отклика Y, b₁ – оценка линейного эффекта, b₂ – оценка квадратичного эффекта.

Построим квадратичный тренд путем добавления линии тренда на график с исходными данными (рис. 10).

Рис. 10. График квадратичного тренда для предсказания реальных доходов компании Wm. Wrigley Jr.

Как показано на рис. 10, уравнение линейной регрессии: Y =513,05 + 40,686Х + 0,2526Х 2 , где началом координат является 1982 год, а шаг переменной X равен одному году. Этот график аппроксимирует временной ряд почти так же, как и линейный тренд. Скорректированный коэффициент r 2 равен 0,965 (рис. 11), а t-статистика, учитывающая вклад квадратичного эффекта, равна 0,656 (соответствующее р-значение равно 0,521).

Рис. 11. Модель квадратичного тренда реальных годовых доходов

Модель экспоненциального тренда.Если временной ряд является возрастающим, а относительное изменение данных — постоянным, можно применять модель экспоненциального тренда. Учитывая сложность формул ограничимся только графическим анализом. Для этого на график с исходными данными добавим линию экспоненциального тренда, а также выведем на график уравнение тренда и параметр r 2 (рис. 12).

Рис. 12. График экспоненциального тренда для предсказания реальных доходов компании Wm. Wrigley Jr.

Экспоненциальная модель аппроксимирует временной ряд почти так же, как линейная и квадратичная модель. Скорректированный коэффициент r 2 равен 0,960, в то время как для линейной модели этот коэффициент равен 0,966, а для квадратичной – 0,965.

Дата добавления: 2015-08-17 ; просмотров: 1106 | Нарушение авторских прав

Содержание

Расчет параметров линейного и квадратического тренда для показателей x и y
Линия тренда в Excel на разных графиках
Добавление линии тренда на график
Уравнение линии тренда в Excel
Линейная аппроксимация
Экспоненциальная линия тренда
Логарифмическая линия тренда в Excel
Полиномиальная линия тренда в Excel
🎥 Видео

Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Расчет параметров линейного и квадратического тренда для показателей x и y

Для расчета параметров уравнений линейного и квадратического тренда построим вспомогательную таблицу.

Таблица 9. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Условное обозначение времени

Формулы для расчета параметров линейного тренда:

Читайте также:

Quot;Я могу обратиться за помощью».
А) Определение прямоугольных координат с помощью циркуля (линейки)
Алгоритм метода множителей Лагранжа
Анализ, отчетность, прогнозирование, профилактика травматизма и профессиональной заболеваемости на производстве
Б) Обнаружение с помощью химических средств
Базовый и производный классы. Конструкторы производного класса. Перегрузка методов при наследовании. Алгоритм выбора перегруженного метода.
Бастилию с помощью письма под чужим именем, в котором

Формулы для расчета параметров квадратичного тренда:

Подставляя в эти формулы все суммы, рассчитанные в последней (итоговой) строке вспомогательной таблицы 4 (Σy =7200320 , Σt 2 = 28 Σt 4 =196, Σyt = 10549215, Σyt 2 = 35198473 ) , получаем следующие результаты:

Линейный тренд y

Квадратический тренд y

Аналогичным образом рассчитаем параметры уравнений линейного и квадратического тренда для показателя x.

Таблица 10. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Условное обозначение времени

x*t

x*t 2

Линейный тренд x

Квадратический тренд x

х^^ = b₀ + b₁* t + b*t 2

Чтобы выбрать, какое из уравнений тренда (линейное или квадратическое) лучше описывает исходный ряд данных, строится вспомогательная таблица для расчета так называемой ошибки аппроксимации, которая находится по формуле:

– исходные значения уровня ряда;

– расчетные значения уровня ряда; т.е. f(t), где f(t) – уравнение соответствующей функции.

Таблица 11. Вспомогательная таблица для расчета ошибок аппроксимации

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Линия тренда в Excel на разных графиках

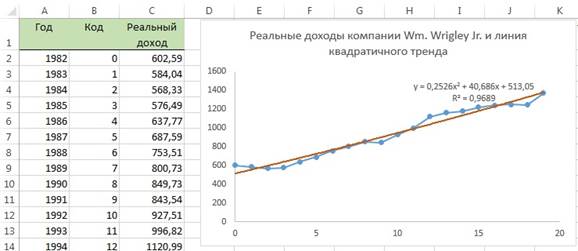
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.

Рассмотрим, как добавить линию тренда на график в Excel.

Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Добавление линии тренда на график

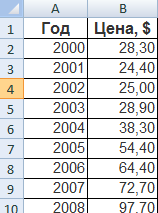
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:

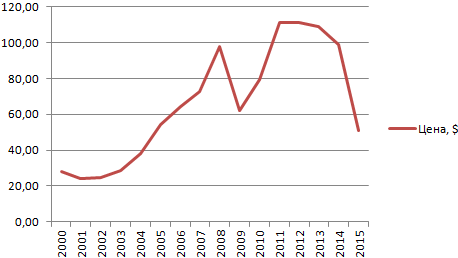
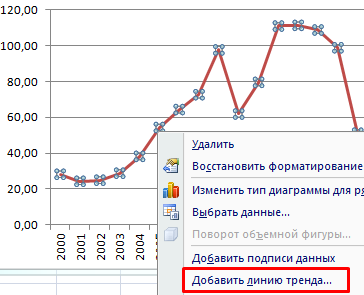
Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
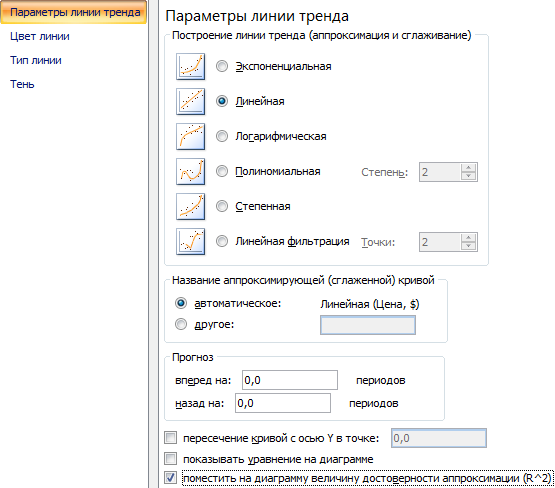
Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
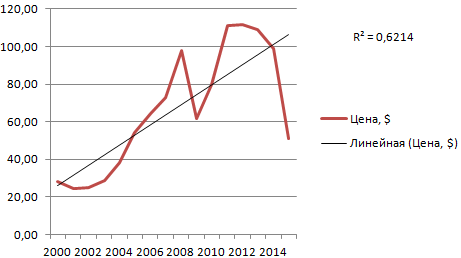
На графике появляется косая линия.

Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.

Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.

Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:

лепестковый;
круговой;
поверхностный;
кольцевой;
объемный;
с накоплением.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Уравнение линии тренда в Excel

В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.

Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.

Линейная аппроксимация

Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.

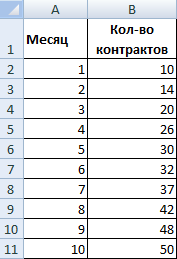
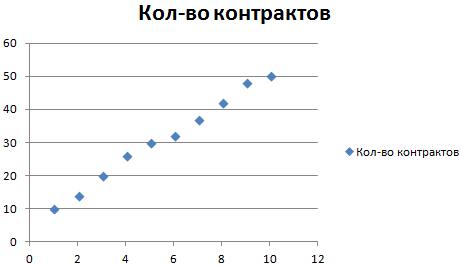
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:

На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):

Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).

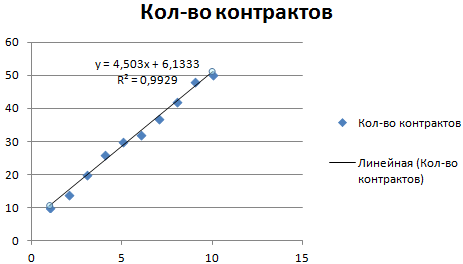
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:

y = 4,503x + 6,1333

где 4,503 – показатель наклона;
6,1333 – смещения;
y – последовательность значений,
х – номер периода.

Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.

Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.

Экспоненциальная линия тренда

Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.

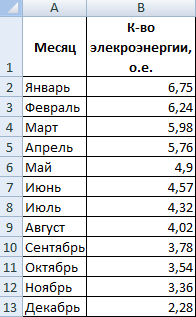
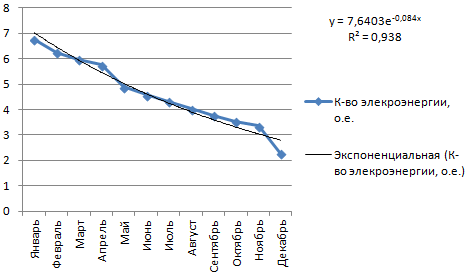
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:

Строим график. Добавляем экспоненциальную линию.

Уравнение имеет следующий вид:

где 7,6403 и -0,084 – константы;
е – основание натурального логарифма.

Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.

Логарифмическая линия тренда в Excel

Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.

На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.

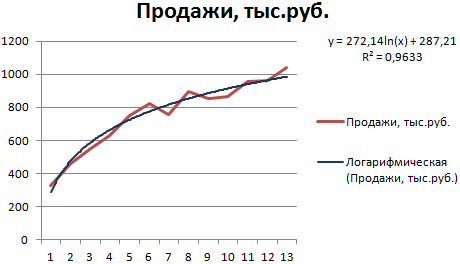
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:

R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.

Период	14	15	16	17	18	19	20
Прогноз	1005,4	1024,18	1041,74	1058,24	1073,8	1088,51	1102,47

Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.

Полиномиальная линия тренда в Excel

Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.

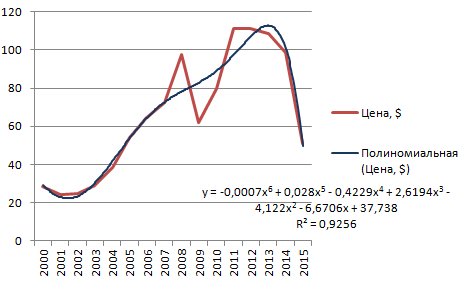
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).