Построение кривой по уравнению в creo

Видео:Построение кривой в полярной системе координатСкачать

Создание чертежей в Creo Parametric 2.0

В гибкой области данных можно использовать уравнения, точно так же, как и в моделях. Такая необходимость, в частности, может быть вызвана требованием переопределить какой-либо параметр, не меняя его значение в исходной модели.

Например, имеется такая ситуация: в модели сборки для удобства стандартные детали объединены в сборку, а в гибкой области данных для стандартных деталей установлен атрибут «Рекурсивный». При этом в область данных попадают стандартные изделия из других подсборок, поэтому итоговое количество определённого компонента получается больше, чем на самом деле. Если таких компонентов немного, то можно исправить количество вручную, используя уравнения.

добавляем в гибкую область данных параметр qty

добавляем уравнения
if (asm_mbr_number == “А ААА .000000.000”)
qty = 10
else
qty = rpt_qty
endif

в гибкой области данных, в разделе «Стандартные изделия», выделяем первую ячейку в столбце «Количество», и в меню правой кнопки выбираем «Свойства»

заменяем &rpt.qty на &rpt.rel.qty

Мы сделали следующее: перебирая компоненты, отфильтрованные в гибкую область данных, программа сравнивает для каждого из них значение параметра number с тем значением, которое мы задали. Если условие выполняется, то параметру гибкой области данных qty присваивается значение 10. Если условие не выполняется, параметру qty присваивается значение rpt_qty, в котором хранится автоматически рассчитанное количество компонентов.

Видео:Creo Parametric. Пружины, инструменты Creo, уравнения. Часть 1Скачать

Параметрическое задание кривой

Видео:Creo Parametric. Тороидальный изгиб. Уравнения параметризацииСкачать

Параметрическое задание кривой

• Кривая параметрическая Н°1.Подход к делу problem. So до сих пор мы рассматривали только 2 вида назначений кривых: уравнение v = f (x) (явная задача) или уравнение F (x, y)= O (неявная задача)).Однако теоретическая механика очень естественно приводит к различным видам линий assignments. In дело в том, что

установка движения точки-это средство нахождения положения (то есть координат) любого момента времени t. Чтобы полностью определить движение точки, определите линию, на которой будет находиться точка move. So, в этом примере линии даны с использованием

So например, эквационный х = 2Т г = 3Т-2(1） Людмила Фирмаль

2 равенств (I).Конечно, очень легко получить более знакомые задачи в той же линии. Именно так. Для любого момента x 3x /будет t = — q, t y =-2. Это соединение X и y обеспечивает явное определение линии*).Видно, что эта задача получается путем исключения времени t из Формулы (1). В рассматриваемом

примере, тот факт, что переменная T показывает время не играет никакой роли. Например, предположим, что следующие X и y зависят от вспомогательных переменных: х = Т-ФЛ, г = т Изменение его даст вам различные точки(.x, комбинация которых состоит из нескольких линий. значение t обозначается равенством t = x-1 с соответствующим значением x, поэтому y =(x-I) 1 для

• любой точки линии, и я получил явную задачу линии. Из этого видно, что вы обрабатываете 1 пару болтов. Чтобы суммировать вышесказанное, пара уравнений Где t-вспомогательная переменная, определяющая lnnnu. Способ определения этой линии называется параметрическим, а переменная t называется

параметром. за исключением t, вы получаете нормальное (явное или неявное) уравнение для той же строки. Замечание. Если функция Людмила Фирмаль

и последовательным в интервале[i, b]), является непрерывной кривой, поскольку она также может Параметрические уравнения для окружностей и эллипсов. Рассмотрим окружность с радиусом R, центрированную вокруг начала координат

(рис.181).Положение любой точки M в этой окружности полностью определяется установкой угла f, который образуется осью Ox и радиусом OM. It естественно выразить координаты x и y точки M под этим углом. Из рисунков это сразу понятно (2） х = р COS в ТТ г = РС НТ. Эти уравнения (*) являются параметрическими

уравнениями окружности. Параметр T может быть изменен с-oo на — | — oo, но если вы хотите получить каждую точку круга по 1 разу, достаточно пройти t через зазор. Однако, это более удобно для обработки закрытых пробелов. Так, т, как правило,

изменяется в пределах 0 ^ / ^ 2ir, но точка с получает в 2 раза. T= 0 и в = 2ir. Чтобы получить нормальное уравнение окружности, необходимо исключить параметр T из (2).Это проще всего, если вы возьмете уравнение (2) на 2 квадрата и добавите результат. Очевидно, это приводит к известному уравнению Найти

параметрическое уравнение эллипса (3） Полезно помнить, что он получается из круга * * + > ■ = A (4)рисунок 181. Имеют диаметр с большой осью эллипса, иногда используют сжатие、 То есть любая точка M в эллипсе(3) берется из точки N в окружности (4). Б Ордината точки Н В соответствии с вышеизложенным

параметрическое уравнение окружности(4) имеет вид x = acos/, ^ = asin/.Но тогда понятно, что параметрическое уравнение (3) эллипса получается умножением. форма ординаты y имеет вид） (5） * = acosf, г = БС НТ. Чтобы получить все точки овала, достаточно

изменить Т выпускного вечера. Жуткий 0 ^ t ^кроме того, каждая точка эллипса, кроме точки (a, 0), получается только 1 раз, а точки(a, 0) — 2 раза (t = 0 и t = 2k).Если мы разделим первое уравнение (5) на a, а затем разделим 2-е уравнение на b, то полученное уравнение будет добавлено на 2 и станет каноническим уравнением эллипса(3).

Сравнение параметрических уравнений окружности и эллипса дает удобный метод построения любого числа точек в эллипсе. То есть, пара уравнений х-acoet, у = грех Т(6） U определяет окружность с радиусом A вокруг начала координат и пару уравнений х = б сое т, у = B грех Т(7） — Окружность b с тем же центром и радиусом; чтобы получить точку (l, y), как показывает уравнение (5), p / 82.Если

вы лежите на овале, вам нужно найти x Используйте первое выражение(6) и 2-е выражение (7) с y. но эти xn-y легко найти графически, так как в формулах (6) и (7) параметром T является угол наклона радиус-вектора точки относительно оси Ox. So, чтобы составить точку M (q, y) эллипса (5), нарисуйте окружность (6) и (7)

и нарисуйте луч на оси Ox под углом t от начала координат. Найдите точки A и B пересечения этого луча и ранее упомянутой окружности и проведите через них прямую линию, параллельную оси, вы получите точку M (см. Рисунок 182).П°3.Циклоида * важные

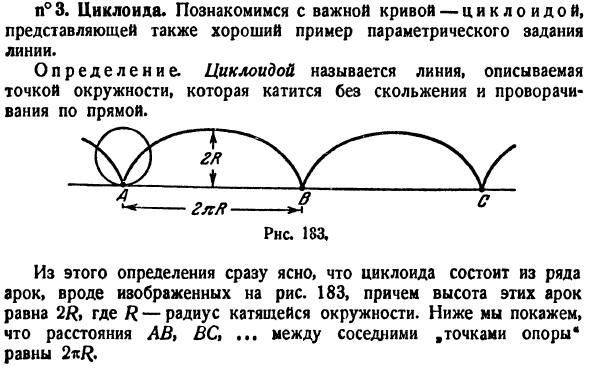
кривые-давайте познакомимся с циклоидой. Это также хороший пример параметрического определения линии. Определение циклоида представляет собой линию, которая представлена точкой окружности, которая катится без скольжения или вращения Из этого определения сразу видно, что циклоида состоит из ряда дуг, как

показано на рисунке 1. 183, высота этих арок равна 2R. R-радиус окружности. Ниже расстояние между соседними точками разворотаAB, BC,…равно 2π/?Это значение по умолчанию. Найдите параметрические уравнения циклоиды. В качестве оси Ox возьмите прямую линию, по которой катится круг, и для начала координат

возьмите положение точки M, которая представляет собой циклоиду острия в этой точке. Эта точка находится на оси Ox. Нарисуйте этот момент как первый момент, вращающийся круг в первый момент, а затем второй. t представляет собой угол, образованный в момент t радиусом вращающейся окружности, направленной

к точке A окружности, которая касается точки I и оси Ox, представляющей циклоиду. (Рисунок 184) радиус CXM и u ° С / а возьмем этот угол т. 184. Попробуйте параметр 8a Через него отрегулируйте точки x и y м-циклоиды. Что касается координат Y, то это довольно просто. г => ВМ = объявление = ОБК-CjZ)= /? — R cos t.

(8） Чтобы найти абсциссу X, нужно рассмотреть эквивалентность отрезка OA и дуги AM. OA = AM. (9 )） При таком равенстве окружность не будет скользить или вращаться. Следующий метод проверки эквивалентности очень очевиден(9): представьте себе катящийся круг, выполненный в виде деревянного кольца. Накройте этот обруч лентой, которая не растягивается, прибив ее правый край гвоздем

к точке O оси Ox, а левый край-к обручу. При вращении обруча лента начинает растекаться по оси Ox, и в момент t отсечение оси OA закрывается той частью ленты, которая упала вниз. С дугой AM обруч. Это*) доказывает(9). еще проще: t-значение угла AC% M, так как это Радиан、 AM = Rt Так… x = OB = OA-BA = AM-MD = Rt-Rsint (10） Если

сравнить (8)и(10), то получим параметрическое уравнение циклоиды х = р(т-Син т), г = р (- стоимость). Параметр Т может изменяться от-ОО до-Е-ОО. Пересечение начала координат и ближайших к нему справа циклоид соответствует значению Ox = t * 2.Это происходит потому, что круг качения приобретается после 1 rotation. In в этом случае

t будет n; = 2nR. In кроме того, из (11) видно, что координаты (π/,, 2/) находятся в высшей точке соответствующего cycloid. To будьте осторожны невозможно представить Y в качестве одной из основных функций Икс. И от x до y возможно| f = Arccos ^ l, но результат Формула очень трудоемкая. Параметрическое уравнение

проще. в N°4.Эвольвента circle. In в теории зацепления используется кривая, называемая эвольвентой окружности. Эвольвента окружности определения-это линия, которая описывается точкой нити и расстегивается от этой окружности, пока она прочно растянута. Предполагается, что нить неэластична и предварительно обмотана вокруг вышеуказанных кругов. Найти параметрическое

уравнение для эвольвенты circle. To сделайте это, поместите начало координат в центр круга и нарисуйте ось Ox Ноль ноль В тот момент, когда нить еще полностью обмотана вокруг окружности, точка окружности, в которой расположена точка, описывающая эвольвенту. Рисунок 185 эта точка обозначается A. 185 показывает положение потока виртуальной машины в некоторой точке в time. So, здесь B-

точка, в которой нить исчезает из окружности, а M-точка, в которой она описывает эвольвенту. Радиус окружности? Угол наклона оси Ox и Луча OB представлен через t. поскольку нить не является растяжимой、 Отрезок VM равен дуге AB окружности. То есть, BM = RT. обратите внимание, что нить остается прочно натянутой, поэтому она спускается по касательной от окружности. Таким образом,

нить VM перпендикулярна радиусу органического вещества. Поэтому углы AOB и MBD равны углам, где каждая сторона перпендикулярна друг другу. Следовательно,£МБД = T, и из треугольника МВС См = РТ грех ЦБ = стоимость РТ. Теперь вы можете легко найти X и y координаты точки м. Другими словами、 х = ое = ОД + де = ОД-ТСМ = стоимости Р + РТ грех г = ВС = ДК = ДБ-КБ = Р грех Т-РТ стоимость. Рисунок 185.Наконец. х = /?(потому что * — Ф — * грех/),; г = р (т Син-/ Кос Т), (’ Где: 0 f > = » K0(13） В точке M (x, y), соответствующей значению параметра T. To сделайте это, дайте

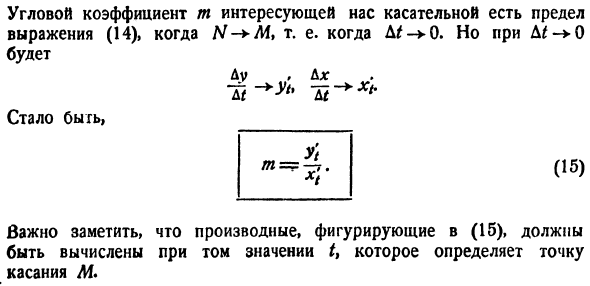
t приращение At и в результате получите ту же самую точку кривой AfCtf-J-A * » Y + AC) (13).Угловой коэффициент Т * Секущий MN равен или равен Важно отметить, что производная, фигурирующая в (15) , должна быть рассчитана для величины t, определяющей контакт M. Угловой коэффициент m интересующего тангенса является

пределом формулы (14) для N — + M, то есть, но так как D * — > 0 Вы будете Работать ДД： (15 )） Так… Образцы. Нарисуйте касательную к кривой + г = Тл-7т(16） Очки*)А!(2). Решение. Координаты точки M определяются из(16). xi = 17, y%=2.In сложение, x = bP—4/, y = 4P-7.So, t = 2 — Это X / = 20, yt = 25, угловой коэффициент Желаемый тангенс. Форма искомого уравнения имеет вид y-2 = 4 (l-17> Замечание.

Приведенная выше строка g:=?( * ), Y =φ (f), функция равна (t), φ (/).Если эти функции не только непрерывны, но и имеют непрерывные производные от y’0, то, как показывает уравнение (15), кривая имеет определенную касательную в каждой точке, и ее положение непрерывно изменяется с изменением контакта.

Кроме того, указанные касательные никогда не будут параллельны оси Oy. Учитывая, что координаты x и y полностью равны, линии x =

.Где f (/j u f ( / ) имеет непрерывную производную、 а В частности, под это определение подпадает линия y = f ( * ), где f (x) имеет непрерывную производную. Где роль параметра T-абсцисса ш=■»+*?> ми- Теперь зададим следующие общие вопросы: пусть

x и y зависят от вспомогательных переменных t, как показано в (13). в первом выражении (13) обозначим t из x, а затем присвоим его 2-му выражению, вы увидите, что y является функцией x, то есть y = f(x).Попробуйте найти производную этой функции. Для этого достаточно вспомнить, что интересующей нас производной является только угловой коэффициент касательной прямой y = / ( * ),

а ее параметрическим уравнением является уравнение (13).Таким образом, она задается формулой(15). Чтобы правильно понять это важное выражение, следует помнить, что точка дифференцирования t справа от (17) является значением параметра, и согласно формуле x = y (t) она соответствует точке дифференцирования x, где Y’x находится. Соотношения(17) легко получить с помощью чисто формальных

вычислений. dypy / ДТ Вау, х]’ Затем попробуйте найти 2-ю производную yx той же функции y = f (x).Это легко сделать, используя формулу (17).То есть он временно представляет y’X с Z. А затем… ** ух-з» (17) Значение (18） Однако, поскольку Z = yx = — m、 / ГМ-ГМ Узнайте, наконец, из (18)и (19) Образцы. Установите вогнутое направление

кривой х =(* + 3Т + л> г = 2Т * — (21） В точке Af (l). Решение. Из (21), x’f = 2t + 3, x? = 2,г = г г! = 12 /.Итак, если t = 1, то это выглядит так:= jc / = 2, y ’ 0, кривая точки M (21) направлена вогнутой поверхностью вверх.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:массив по кривой дополнение CREO 3.0Скачать

Меню видеокурса

Посмотреть или скачать описание уроков базового курса в формате .pdf

Видео:Creo Parametric. Инструмент Протянуть. Протягивание постоянного сеченияСкачать

Часть 1. Базовый курс твердотельного моделирования

Видео:Creo Parametric. Урок - Построение сложных эскизов.Скачать

(Creo Parametric 2.0-8.0)

Урок 1. Знакомство с интерфейсом Creo Parametric 2.0 (15 мин)
Главное меню. Инструментальная лента. Панель быстрого доступа и ее настройка. Навигатор папок. Web-навигатор. Графическое окно.
Команды манипулирования моделью в графическом окне: Вращение, Перемещение, Масштабирование, Прецизионное масштабирование.
Панель управления графикой и ее свойства. Кнопка стандартные виды. На основе всех стандартных видов могут быть созданы их новые ориентации, кроме стандартной ориентации, а также создание пользовательских ориентаций.
Дерево модели. Сопоставление команд «Править» и «Править определение».
Понятие о сессии работы в Creo Parametric. (Все файлы, открытые/созданные в процессе работы с Creo за время сессии, загружаются в оперативную память компьютера и находятся там все время, даже если они были закрыты в Creo. Файлы не будут сохранены на диск, пока Вы их сами не сохраните с помощью соответствующей команды).
Очистка оперативной памяти компьютера в Creo Parametric.
Версии сохраненных файлов. Порядок удаления старых версий файлов.
Основные расширения файлов Creo Parametric. Типы файлов.

Урок 1. Знакомство с интерфейсом Creo Parametric 8.0 (15 мин)
Главное меню. Инструментальная лента. Панель быстрого доступа и ее настройка. Навигатор папок. Web-навигатор. Графическое окно. Демонстрация работы левой и правой кнопок мыши в дереве модели файла открытого в версии Creo Parametric 2.0 и последующая демонстрация этих действий в 8-й версии.
Команды манипулирования моделью в графическом окне: Вращение, Перемещение, Масштабирование, Прецизионное масштабирование.
Панель управления графикой и ее свойства. Кнопка стандартные виды. На основе всех стандартных видов могут быть созданы их новые ориентации, кроме стандартной ориентации, а также могут быть созданы новые ориентации с произвольным наименованием.
Дерево модели. Мини-панель инструментов и ее настройка. Панель контекстного меню и ее настройка. Сопоставление команд «Править» и «Править определение».
Понятие о сессии работы в Creo Parametric. (Все файлы, открытые/созданные в процессе работы с Creo за время сессии, загружаются в оперативную память компьютера и находятся там все время, даже если они были закрыты в Creo. Файлы не будут сохранены на диск, пока Вы их сами не сохраните с помощью соответствующей команды).
Очистка оперативной памяти компьютера в Creo Parametric.
Версии сохраненных файлов. При открытии файла Крео показывает всегда последнюю версию, но при каждом сохранении файла в процессе работы сохраняется его новая версия. Порядок удаления старых версий файлов.
Основные расширения файлов Creo Parametric. Типы файлов.

Урок 2. Начало работы (14 мин).

Многооконный режим работы. Порядок начала работы. Выбор или создание рабочей папки (директории). Установка рабочей директории является необходимым моментом в работе с Creo, так как именно в эту директорию система будет сохранять все созданные за время сессии файлы. Это важно по двум причинам. Во-первых, в этом случае не нарушается ассоциативные связи, а во-вторых, не будет возникать проблем при переносе проекта на другой компьютер. Свойства рабочей папки (директории). Синтаксис названия модели. Выбор шаблона свойств и параметров модели. Первое знакомство с панелью свойств модели. Упражнение по созданию модели заготовки болта. Получение объемного тела и полости при помощи операции «Вытянуть».

Урок 2д. Дополнение к уроку 2 «Начало работы» (4 мин).

Новый способ активации окон при двухоконной работе. Применение внутренних эскизов для создания твердотельной геометрии.

Урок 3. Работа в среде эскизов (15 мин).

Главное меню и инструментальная лента среды эскизов. Дерево слоев. Группа команд создания эскиза. Ограничения (связи) элементов эскиза. Редактирование эскиза. Идентификаторы в эскизе. Наследование идентификаторов. Сильные и слабые размеры. Конфликты размеров. Масштабирование размеров.
Урок 3д. Дополнение к уроку 3 «Работа в среде эскизов» (14 мин).
0 мин 0 сек — Идентификаторы ограничений в Creo Parametric 8.0. Работа с новой кнопкой графической панели «Фильтры показа среды эскиза».
1 мин 20 сек – Нанесение размера длины отрезка и его проекций на оси координат
2 мин 20 сек – Группа команд «Подготовить» на ленте. Кнопка настойка эскиза в среде эскиза, кнопка «Привязки» и кнопка «Вид эскиза».
3 мин 00 сек – Кнопка «Импорт». Назначение и демонстрация работы. До 7-й версии название этой кнопки «Файловая система».
4 мин 30 сек – Отличие набора опорных элементов: ось, точка, система координат от набора: ось, точка, система координат в группе «Создание эскиза».
4 мин 50 сек – Кнопка «Режим конструирования».
5 мин 30 сек – Расширенные сведения о работе с группой команд «Создание эскиза»: касательный отрезок, виды четырехугольников (наклонный, центральный, параллелограмм), виды окружностей, виды дуг (касательная к трем, концентричная, коническая), виды скруглений (круглое и круглое с отсечением, эллиптическое и эллиптическое отсечение), виды фасок.
8 мин 00 сек – Кнопка «Текст». Пример создания текста.
9 мин 00сек – Кнопки «Смещение» и «Утолстить. Примеры применения.
10 мин 00 сек – Кнопка «Угол» и кнопка «Разделить». Примеры применения
11 мин 10 сек – Кнопка «Периметр». Пример расчета периметра фигуры, выделение управляющего размера и его роль
12 мин 00сек – Роль кнопок «Подсветить закрытые концы» и «Закраска замкнутых контуров»

Урок 4. Инструменты «Вытянуть», «Вращение», «Ребро» (16 мин).

Создание модели коленчатого вала. Операция «Вытянуть» в режиме удаления материала. Окно привязок. Создание винта с использованием инструмента «Вращение». Создание базовых плоскостей. Построение прямолинейных и криволинейных ребер жесткости.

Урок 4д. Дополнение к уроку 4 «Ребра жесткости» (8 мин)

Добавлены пример создания ребра жесткости по траектории, а также пример создания кругового ребра профиля.

Урок 5. Инструменты «Протянуть», «Протягивание по спирали», «Плавное сопряжение» (12 мин).

Создание траектории и сечения протягивания и плавного сопряжения.

Урок 6. Безэскизные_фичеры (20 мин).

Встроенные объемные примитивы. Простые и стандартные отверстия. Диалоговая панель безэскизных фичеров. Координаты местоположения отверстий. Расширенные опции создания стандартных отверстий. Виды скруглений. Фаски и виды размерных схем фасок. Построение уклонов. Тонкостенные детали. Ребро траектории.

Урок 7. Создание шестерни с эвольвентным зубом (12 мин).

Панель уравнений. Уравнения эвольвенты. Создание кривой по уравнению. Круговой массив.

Урок 8. Создание опорной геометрии (10 мин).

Панель управления графикой. Панель «Опорная плоскость». Создание дополнительных плоскостей под различными углами к базовым координатным плоскостям и другим дополнительным плоскостям. Создание опорных осей. Создание опорных точек. Создание опорных плоскостей по опорным точкам.

Урок 9. Массивы (12 мин).

Виды массивов. Прямоугольные, концентрические и смешанные массивы. Лидер массива и его члены. Управление размерами и ориентацией членов массива. Одномерные и двухмерные массивы.

Урок 10. Пружины сжатия (6 мин).

Создание пружин сжатия с поджатыми витками на концах и опорными параллельными плоскостями.

Урок 11. Пружины растяжения (9 мин).

Создание зацепов пружин протягиванием по пространственным кривым, полученным проецированием плоской кривой на цилиндрическую поверхность.

Видео:Решить дифф. уравнение и построить интегральные кривыеСкачать

Часть 2. Создание чертежа.

Урок 12. Создание чертежа. Модель (9 мин).

Создание модели детали «Хвостовик штампа». Создание простых и сложных сечений. Штриховка и ее редактирование

Урок 13. Формат чертежа и свойства среды создания чертежа (12 мин).

Выбор формата. Особенности главного меню и интерфейса среды создания чертежа. Создание главного вида и его проекций. Панель свойства чертежа. Создание дополнительных и выносных видов. Редактирование штриховки.

Урок 14. Создание размеров (13 мин).

Создание заданного изометрического вида на чертеже. Создание именованных видов на модели и чертеже. Вкладка главного меню «Аннотации». Панель аннотаций модели. Нанесение размеров. Упорядочивание размеров. Управление размерными и выносными линиями. Нанесение размеров от общей базы. Создание ординатных размеров. Создание размеров на выносном виде.

Урок 15. Создание чертежей. Допуски на размеры (12 мин).

Создание осевых линий. Корректировка длин осей. Создание эскиза в среде чертежа. Создание вспомогательной линии центров отверстий. Панель свойства размера и ее вкладки: Свойства, Изображение, Стиль текста. Вставка символов. Суффиксы и префиксы размерных чисел. Специальные символы для установки нижнего и верхнего допуска. Системы допусков ANSI и ISO. Опции управления системами допусков для линейных и угловых размеров, а также выбор допусков в зависимости от класса точности класса точности.

Урок 16. Создание чертежей. Геометрические допуски (11 мин).

Геометрические допуски, т.е. отклонения и допуски формы и расположения поверхностей. Обозначения баз, создание базовых и контрольных размеров. Создание допуска на концентричность. И части рамки, определяющей допуск на концентричность. Заполнение стандартной рамки допуска на концентричность с указанием символов «По минимуму массы», «По максимуму массы», «Без указания символов».
Нанесение символов шероховатости поверхности с указанием способа обработки поверхности и без указания, с удалением материала (резанием), без удаления материала (штамповкой). Требования к шероховатости неуказанных поверхностей.

Урок 17. Создание чертежей. Текстовые надписи (12 мин).

Создание надписи непосредственно на чертеже или из файла. Редактирование текста. Создание текста заключенного в рамки. Создание текста связанного с элементами чертежа. Надстрочный и подстрочный текст в заметке. Создание заметок с параметрическими данными. Знак амперсанд и пользовательские параметры.

Урок 18. Создание чертежей. Шаблон чертежа (15 мин).

Ячейки углового штампа с постоянными и параметрическими записями. Панель «Параметры модели». Добавление новых параметров, необходимых для заполнения углового штампа чертежа. Панель массовые свойства. Расчет массы детали.

Урок 19. Создание чертежей. Дерево слоев (8,5 мин).

Обзор автоматически созданных слоев. Создание нового слоя. Статус слоя. Полезные свойства функционала слоев. Сохранение статуса. Свойства сохраненного и несохраненного статуса слоя. Связь между слоями модели и чертежа.

Урок 20. Создание чертежей. Таблицы (12 мин).

Вкладка главного меню «Таблица». Создание таблиц. Управление размерами ячеек таблицы. Выделение ячеек, строк и столбцов таблицы. Объединение ячеек. Внесение заметок в таблицу. Редактирование стиля текста. Добавление и удаление строк и столбцов. Создание таблицы координат центров отверстий массива (или других однотипных элементов детали) относительно заданной системы координат.

Урок 21. Сборка с закреплениями (12 мин).

Создание новой сборки. Статус детали в сборке. Типы закреплений. Горячие клавиши манипулирования деталью в сборке. Вспомогательное окно для манипулирования деталью в сборке. Открепление и прикрепление вспомогательного окна в файле config.pro

Урок 22. Создание спецификации (14,5 мин).

Понятие гибкой области данных. Команда добавления гибкой области данных. Системные параметры гибкой области данных. Иерархический список параметров. Порядок заполнения параметрами ячеек таблицы с гибкими областями данных. Атрибуты гибкой области данных. Создание выносок позиций деталей на различных видах. Редактирование выносок. Упорядочивание позиций выносок деталей сборки.

Видео:PTC Creo Parametric. Урок №6. Вращение, протягивание и сопряжениеСкачать

Часть 3. Создание библиотек

Урок 23. Создание библиотек стандартных деталей по типу «с приращениями» (10 мин).

Таблица семейств. Символьное и смысловое отображение размеров базовой (родовой) модели таблицы семейства. Создание шапки таблицы семейства. Выбор условий размножения базовой модели. Создание параметров семейства при помощи уравнений. Управление геометрий членов семейства.

Урок 24. Создание библиотек стандартных деталей с использованием уравнений (13 мин).

Группирование размерных параметров. Ввод уравнений для генерации параметров пользователя. Логический оператор if.

Видео:Уравнения и таблицы семейств в Creo ParametricСкачать

Часть 4. Проектирование механизмов «сверху-вниз» и элементы оптимизации.

Урок 25. Проектирование механизмов «сверху-вниз». Скелетные модели (16 мин).

Создание пространства сборки, подсборки и их структуры. Понятие скелетонах. Неразмещенные компоненты скелетных моделей. Многократные скелеты. Редактор конфигурации и опция multiple_skeletons_allowed. Создание ссылок размещения

Урок 26. Создание деталей на основе скелетных моделей (16,5 мин).

Связи в скелетонах. Скелет движения. Копирование геометрии. Создание твердых тел из скелета движения. Соединения механизма – штифт, ползун. Проверка сборки на движение

Урок 27. Оптимизация коленчатого вала (13 мин).

Цели оптимизации – устранение дисбаланса и минимизация массы. Панель свойства модели. Выбор единиц измерения. Работа с панелью Массовые свойства. Определение координат центра тяжести. Создание системы координат в центре тяжести. Работа в панели измерений. Добавление столбцов в дерево модели. Анализ чувствительности местоположения центра тяжести к изменению различных размеров вала и построение графиков чувствительности. Панель оптимизации. Выбор опций в панели оптимизации.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Часть 5. Углубленный курс создания моделей со сложными поверхностями (Часть 1).

Урок 28. Инструмент «Протянуть». Углубленный курс. Ч.1. (13,5 мин)

Инструмент «Протянуть». Углубленный курс. Ч.1 (Advanced Sweep. Р.1)
Локальная система координат протягиваемого тела. Х-траектория. Протягивание по нормали к первоначальному сечению. Протягивание сечения при постоянном направлении нормали к произвольной плоскости. Протягивание по криволинейной траектории. Построение пространственной кривой пересечением плоских кривых. Протягивание по нормали к проекции пространственной кривой на различные плоскости. Опции «Удлинить до» и «Отсечь»

Урок 29. Инструмент «Протянуть». Углубленный курс. Ч.2 (13 мин).

Построение и редактирование сплайна. Построение объемного тела с криволинейной поверхностью. Протягивание по криволинейной поверхности. Пример создания одно- и многозаходной резьбы с заданным профилем.

Урок 30. Инструмент «Протянуть». Углубленный курс. Ч.3 (10 мин)

Создание уравнений траектории протягивания. Использование встроенной функции trajpar. Протягивание по траектории заданной уравнением меняющегося сечения. Использование встроенной функции evalgraph. Сетка в среде эскиза.

Урок 31. Инструмент «Протянуть». Углубленный курс. Ч.4 (15 мин).

Практика совместного использования функций evalgraph и trajpar:
— для создания кругового паза на цилиндрической заготовке с участками подъема, спуска и площадками выстоя;
— для создания турбинной лопатки.

Урок 32. Косозубое зацепление (11,5 мин).

Протягивание под углом к цилиндрической поверхности. Создание косозубых шестерен

Урок 33. Механизм косозубого зацепления (15,5 мин).

Создание несущего тела (базового элемента). Порядок создания соединения «Штифт». Смысл значения регенерации. Создание сервопривода вращения. Кинематический анализ зубчатого зацепления. Запись файла с анализом. Воспроизведение работы зубчатой пары

Видео:PTC Creo Parametric. Урок №4. Создание эскиза.Скачать

Часть 6. Практика. Создание проекта привода

Урок 34. Проект. Ч.1 (13 мин).

Исходные данные для расчета привода ленточного конвейера. Результаты расчетов. Сборка быстроходного вала. Временное отключение соединения. Сборка тихоходного вала.

Урок 35. Проект. Ч.2 (18,5 мин)

Установка подсборок быстроходного и тихоходного валов. Создание скелетона нижней части корпуса редуктора. Создание твердотельной модели нижней части корпуса редуктора на основе скелетона. Установка неразмещенной модели нижней части корпуса в сборку. Новый вариант создания ребра жесткости по траектории.

Урок 36. Проект. Ч.3 (16 мин).

Создание скелетона верхней части корпуса редуктора. Создание твердотельной модели верхней части корпуса редуктора на основе скелетона. Установка неразмещенной модели верхней части корпуса в сборку. Устройство смотрового окна редуктора

Урок 37. Проект. Ч.4 (15 мин).

Корректировка модели верхней части корпуса. Создание простых отверстий для сборки половин корпуса редуктора. Создание резьбовых отверстий для крепления крышки смотрового окна и фланцев. Выбор членов массива для исключения из конструкции. Установка в сборку крышки смотрового окна. Создание в нижней части корпуса бобышки для установки указателя уровня масла. Создание отверстия для слива масла.

Урок 38. Проект. Ч.5 (14 мин).

Изменение цвета деталей сборки и стиля изображения. Установка в сборку фланцев и указателя уровня масла. Создание интерфейса компонента. Автоматизация установки болтов с использованием интерфейса. Создание сборки привода

Урок 39. Проект. Ч.6 (14,5 мин).

Создание механизма «Зубчатое зацепление». Создание ременной передачи. Создание детали «Ремень». Создание сервоприводов для зубчатой пары и ременной передачи. Воспроизведение работы привода. Вывод результатов кинематического анализа в графическом виде. Создание видеоролика для презентации работы привода

Видео:Профили по кривым EFX CREO 3Скачать

Часть 7. Теория и практика создания моделей со сложными поверхностями (Часть 2)

Урок 40. Уравнения в эскизах (9,5 мин).

Управление размерами элементов эскиза при помощи уравнений. Встроенная функция Solve. Задача о выборе размеров тела или его внутренней полости с заданным объемом

Урок 41. Уравнения опорных кривых (10 мин).

Задание кривых в параметрическом и явном виде: прямые, параболы, синусоида, винтовая линия. Использование кривых для получения поверхностей и оболочек

Урок 42. Сопряжение (10,5 мин).

Сопряжение сечений в параллельных и наклонных плоскостях. Сопряжение фичеров, созданных на основе сечений в непараллельных плоскостях

Урок 43. Сопряжение (14 мин).

Сопряжение фичеров, созданных на основе сечений, имеющих различное число угловых точек в непараллельных плоскостях. Сопряжение с точкой. Вращательное сопряжение. Опции «Нормаль» и «Касательность»

Урок 44. Плавное сопряжение (15,5 мин).

Создание настенного светильника.

Урок 45. Методология User—defined features (19 мин).

User-defined features (UDFs) — элементы пользователя. Создание подчиненных и автономных UDFs с учетом наследственной опорной геометрии и геометрии шаблона. Назначение переменных размеров. Размещение UDFs при создании вариантов детали и новых моделей деталей. Применение методологии UDFs на примере создания шпоночного паза и шлицевого соединения.

📺 Видео

Creo Parametric. Инструмент Изгиб по направляющей. Создание накидного гаечного ключаСкачать

Видеоурок 1 по Creo Parametric 2.0Скачать

Creo Parametric. Протягивание по спирали. Создание болта с реалистичной резьбойСкачать

Часть 1. Расчет основных элементов круговой кривойСкачать

Creo Parametric. Чертеж. Сечения видов в чертежах. Местный, ломаный и ступенчатый разрезыСкачать

PTC Creo. Пользовательский анализСкачать