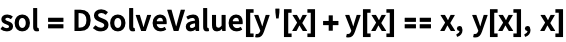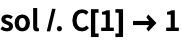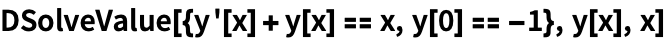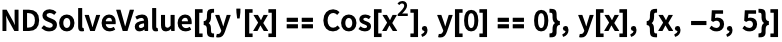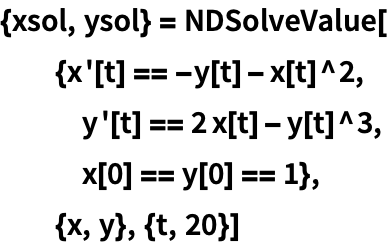Построение графиков дифференциальных уравнений wolfram mathematica

Видео:Видео курс Wolfram Mathematica | Функция Plot | Часть 1/2Скачать

Использование Wolfram Mathematica в решении дифференциальных уравнений

Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского

NovaInfo55, с. 5-9
Опубликовано 20 ноября 2016
Раздел: Физико-математические науки
Просмотров за месяц: 48
CC BY-NC

Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

Аннотация

В статье рассматриваются примеры решения обыкновенных дифференциальных уравнений в системе Wolfram Mathematica.

Видео:Wolfram Mathematica, 1 занятие, осень 2020Скачать

Ключевые слова

Видео:Wolfram Mathematica, 10 занятие, весна 2020Скачать

Текст научной работы

Системы компьютерной математики (Maple, Mathematica, MatLab, Derive и др.) применяются в различных областях науки. Они содержат процедуры для численных и аналитических расчетов, средства программирования, визуализации. В настоящее время пакеты прикладных программ используются не только при решении численных задач, но и при доказательстве теорем. Системы компьютерной математики используются в решении математических проблем в работах Д.С. Воронова, О.П. Гладуновой, Е.С. Корнева, М.В. Куркиной, Е.Д. Родионова, Я.В. Славолюбовой, В.В. Славского, Н.К. Смоленцева, Л.Н. Чибриковой и др.

Система компьютерной математики Wolfram Mathematica является одним из наиболее распространенных программных средств, которое позволяет выполнять численные, символьные вычисления, имеет развитую двумерную и трехмерную графику, а также встроенный язык программирования высокого уровня. Для знакомства с языком программирования Wolfram Language рекомендуется интернет-ресурс Wolfram Language & System «Documentation Center» (http://reference.wolfram.com/language/). Выбирая раздел, можно познакомиться с имеющимися командами для решения задач и с примерами их использования. Примеры использования Mathematica в решении геометрических задач приведены в 4.

Система Mathematica обладает обширными возможностями решения обыкновенных дифференциальных уравнений и их систем в символьном виде. Для этого используется функция DSolve, в алгоритме которой реализовано большинство известных на сегодняшний день аналитических методов.

Пример 1. Решим дифференциальное уравнение и построим график решений при различных значениях постоянной.

Пример 2. Решим уравнение y’=frac

Попытаемся решить уравнение с помощью функции DSolve:

В данном случае функция DSolve не может решить нелинейное уравнение. Поэтому запишем уравнение в виде:

и будем интегрировать обе части уравнения:

Следовательно, общее решение уравнения примет вид

-(-2+y^2)cos y+2ysin y=x-10ln (1-x)+13ln(2-x)+C

Пример 3. Решим дифференциальное уравнение и построим поле направлений и график решения уравнения при различных значениях константы.

Построим таблицу решений, заменив С[1] на a, где a изменяется от -2 до 2 с шагом 0,5:

Отобразим два графика одновременно и покажем, что векторы поля направлений являются касательными к решениям дифференциального уравнения:

Система Wolfram Mathematica используется для решения дифференциальных уравнений не только в математике, но и актуальна в других научных областях. Ее можно применять и в механике, в частности, для решения различных постановок задач, где в качестве математических объектов используются дифференциальные уравнения. В работах [6,7] рассмотрены уравнения движения мембран и акустических сред в виде обыкновенных дифференциальных уравнений. Для их решения может быть использована система компьютерной математики Wolfram Mathematica.

Видео:Математика это не ИсламСкачать

Читайте также

Математическая подготовка студентов в вузе в контексте будущей профессиональной деятельности

Использование прикладных программ при изучении математической статистики

Применение систем компьютерной математики при изучении комплексного анализа

Организация самостоятельной работы студентов в условиях информационно-образовательной среды вуза

Системы компьютерной математики в решении дифференциальных уравнений

Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

Список литературы

1. Букушева А.В. Использование Mathematica для описания геометрии динамических систем // Математика и ее приложения: фундаментальные проблемы науки и техники : сборник трудов всероссийской конференции, Барнаул, 24 — 26 ноября 2015. — Барнаул : Изд-во Алт. ун-та, 2015. С. 248-249.
2. Букушева А.В. Применение Wolfram Language для выделения специальных классов почти контактных метрических структур // Компьютерные науки и информационные технологии : Материалы Междунар. науч. конф. — Саратов : Издат. центр.»Наука», 2016. С. 105-107.
3. Букушева А.В. Использование систем компьютерной математики для решения геометрических задач сложного уровня // Информационные технологии в образовании: Материалы VI Всероссийской научно-практической конференции. – Саратов: ООО «Издательский центр «Наука»». 2014. – С. 76-77.
4. Букушева А.В. Решение учебно-исследовательских задач с использованием систем компьютерной математики // Информационные технологии в образовании: Материалы VII Всеросс. научно-практ. конф. – Саратов: ООО «Издательский центр «Наука»», 2015. С.185-187.
5. Букушева А.В. Учебно-исследовательские задачи в продуктивном обучении будущих бакалавров-математиков // Образовательные технологии. 2016. №2. С. 16-26.
6. Вельмисова А.И. Распространение и отражение гармонических волн в плоском акустическом слое с гибкими стенками в случае разрыва упругих свойств на одной из стенок // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2010. Вып.12. С. 136-140.
7. Вельмисова А.И., Вильде М.В., Кириллова И.В. Распространение и отражение гармонических волн в плоском акустическом слое с кусочно-неоднородными гибкими стенками // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2011. Т.11. №4. С. 68-73.

Видео:Язык Wolfram Mathematica с нуля | #1 Первая программа на wolfram.Скачать

Цитировать

Зинина, А.И. Использование Wolfram Mathematica в решении дифференциальных уравнений / А.И. Зинина. — Текст : электронный // NovaInfo, 2016. — № 55. — С. 5-9. — URL: https://novainfo.ru/article/8754 (дата обращения: 17.02.2022).

Видео:Создание графиков с двумя различными осямиСкачать

Поделиться

Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

Соучредители СМИ: Долганов А.А., Майоров Е.В.

Видео:1. Знакомство с Wolfram Mathematica. "Галопом по Европе" (English subtitles)Скачать

Дифференциальные уравнения

Язык Wolfram позволяет решать обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и уравнения с запаздыванием.

Функция DSolveValue возвращает решение дифференциального уравнения в общем виде:

Out[1]=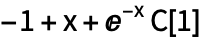

Используем символ /. для замены константы:

Out[2]=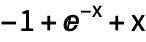

Или добавим начальные условия для получения частного решения:

Out[3]=

Функция NDSolveValue позволяет находить численные решения:

Out[1]=

Объект InterpolatingFunction можно визуализировать без дополнительной обработки:

Out[2]=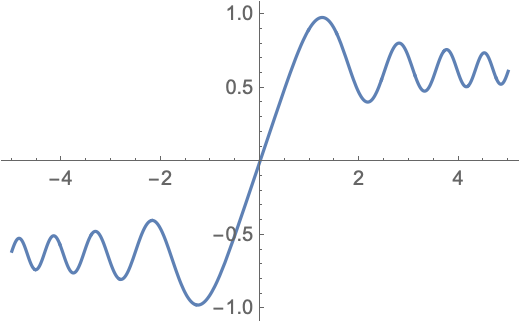

Для решения систем дифференциальных уравнений, необходимо использовать списки для задания уравнений и условий:

(Обратите внимание, что перенос уравнений на новую строку не влияет на результат.)

Out[1]=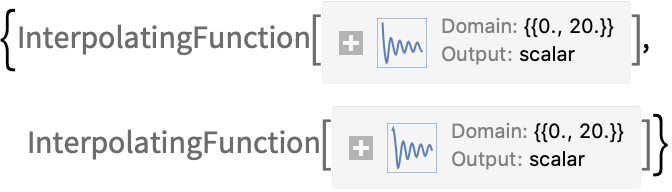

Построим решения системы в виде параметрического графика:

Видео:Wolfram Mathematica, 9 занятие, весна 2020Скачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.

Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.

Чтобы решить дифференциальное уравнение с помощью Wolfram|Alpha достаточно ввести его в систему. ВНИМАНИЕ! Для ввода символа производной используется знак апострофа » ‘ «, но не кавычки (!). Для определенности можно добавить перед уравнением поисковое предписание solve (хотя, во многих случаях, это и не обязательно).

• solve xy’+y=2x

Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.

Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:

Аналогичным образом можно получить решение, например, дифференциального уравнения Бернулли:

• solve 2xy’+y=x^2y^3

• solve y’-2y/x=-x^2y^2

Wolfram|Alpha позволяет также получать решения дифференциальных уравнений второго и высших порядков. Например, так выглядит решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:

• solve y» + 2y’ +y= 54x^2e^(2x)sin(3x)

Или же дифференциального уравнения 3-го порядка: solve y»» = y.

С помощью Wolfram|Alpha возможно получить общее решение дифференциального уравнения, заданного в общем виде:

• solve a*y»(x)+b*y'(x)+c*y(x)=0

Наконец, в некоторых случаях, когда это необходимо,Wolfram|Alpha использует для решения дифференциальных уравнений методы операционного исчисления (преобразование Лапласа):

• solve y»(x)-2y'(x)/x+y(x)=0

Подробное решение этого примера смотрите по этой ссылке.

🌟 Видео

Новое в Wolfram Language | Аналитическое решение уравнений в частных производныхСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Геометрический смысл дифференциального уравненияСкачать

КиЯ 0.10 | Опции функций в Wolfram LanguageСкачать