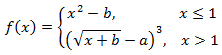Построение графика функции заданной системой уравнений (5 видео)

Построение графика функции заданной системой уравнений

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.

Объединяем уравнения в систему с помощью фигурной скобки:

Содержание

Графический метод
Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
Видео YouTube
Строим график функции, заданный системой уравнений, в EXCEL
Решение (1 ряд данных)
Решение (2 ряда данных)
Решение (3 ряда данных)
Решение системы уравнений графическим методом средствами MS Excel
Основная часть
Заключительный этап урока
🎥 Видео

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки.

Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера.

Пример 1

Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):

Для того чтобы графически решить систему уравнений с двумя переменными нужно:

1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);

Разберем это задание на примере.

Решить графически систему линейных уравнений.

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Пример 2

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы

Пример 4

Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Пример 5

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

Видео YouTube

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Строим график функции, заданный системой уравнений, в EXCEL

history 8 января 2018 г.

Контрольные работы и задания
Диаграммы и графики

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .

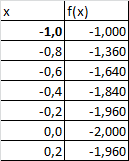
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):

Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

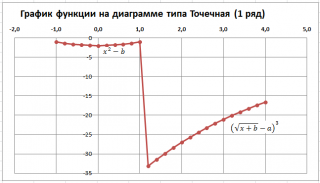
Чтобы построить диаграмму типа Точечная:

выделите любую ячейку таблицы;
во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .

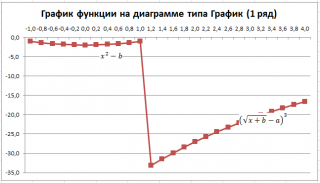
Чтобы построить диаграмму типа График:

выделите любую столбец f(x) вместе с заголовком;
во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .

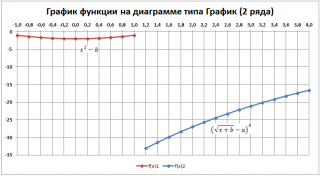
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение (2 ряда данных)

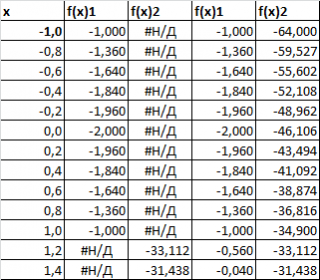
Создадим другую таблицу с исходными данными в файле примера, лист График :

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Видео:Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Решение системы уравнений графическим методом средствами MS Excel

Цели и задачи.

Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
Закрепить навыки создания таблиц и диаграмм.
Научить решать систему уравнений графическим методом, исследовать график функции.

Оборудование урока: компьютеры, мультимедиа проектор.

Программное обеспечение: Windows XP, пакет программ MS Office 2003.

Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.

Запишите в тетради тему урока и укажите дату.

Назовите мне кого из класса сегодня нет.

Давайте вспомним, что такое уравнение, и как его можно решить графически.

Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.

(Учащиеся приводят определения)

Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.

Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).

Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.

Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.

Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.

Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.

Но эту задачу может взять на себя ЭВМ.

Мы воспользуемся возможностями программы MS Excel.

Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Основная часть

Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.

Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.

С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.

И так. Мы запустили программу MS Excel.

Мы хотим разработать таблицу для решения системы уравнений:

Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.

Сформируем начальные данные.

В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.

В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.

Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.

Формулы, которые нам нужно ввести приведены на рисунке.

Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.

Заполните, пожалуйста, в каждой таблице 20-25 строчек.

Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.

Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.

Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.

Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.

Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.

Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.

У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.

Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.

Мы видим, что одно из решений нашей системы уравнений равно -1,5.

Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.

Сколько у вас получилось?

Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.

Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.

Для этого нужно внести изменения в таблицу и расчётные формулы.

Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.

Самостоятельно внесите все необходимые изменения.

Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Заключительный этап урока

Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?

А что легче для вас?

Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.

Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.

Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.