Построение эллипсоида по каноническому уравнению (5 видео)

Построение эллипсоида по каноническому уравнению

8.4. Построение поверхностей

Мы приступаем к изучению формы поверхностей второго порядка, определённых в предыдущем разделе своими каноническими уравнениями. Напомним, что это вторая из двух основных задач аналитической геометрии: зная уравнение поверхности, изучить её геометрические свойства.

Метод, который мы будем применять, называется методом сечений: пересекая поверхность плоскостями, параллельными координатным плоскостям, будем рассматривать линии пересечения и по их виду делать выводы о форме поверхности.

Каноническое уравнение эллипсоида:

Отметим симметрию поверхности: если точка (x, у, z) лежит на эллипсоиде, то и все точки (±x, ±у, ±z) тоже лежат на эллипсоиде. Значит, поверхность симметрична относительно любой из координатных плоскостей. Пересечём эллипсоид плоскостью z = h. Получим линию

Это эллипс, полуоси которого убывают с увеличением |h|. При h = c эллипс превращается в точку, при h > c плоскость z = h не пересекает эллипсоид. Эллипсы получаются и при сечении эллипсоида плоскостями x = h, у = h. Используя эти данные, изображаем поверхность. Числа a, b, c называются полуосями эллипсоида. Если две полуоси равны, то получается эллипсоид вращения. Например, эллипсоид, образованный при вращении эллипса (лежит в плоскости XOZ) вокруг оси OZ. Если a = b = c, то эллипсоид превращается в сферу.

Содержание

Основные поверхности пространства и их построение
Распространенные уравнения плоскостей
Уравнение плоскости в отрезках
Цилиндрические поверхности
Параболические цилиндры
Гиперболические цилиндры
Эллипсоид. Сфера и шар
Коническая поверхность
Эллиптический параболоид
Эллипсоиды
Определение эллипсоида
Плоские сечения эллипсоида
Эллипсоиды вращения
🎥 Видео

Видео:§20 Построение эллипсаСкачать

Основные поверхности пространства и их построение

Данная статья носит справочный характер и по своей структуре очень напоминает материалы о графиках и свойствах элементарных функций. С тем отличием, что вместо «плоских» графиков мы рассмотрим наиболее распространенные пространственные поверхности, а также научимся грамотно их строить от руки. Я довольно долго подбирал программные средства для построения трёхмерных чертежей и нашёл пару неплохих приложений, но, несмотря на всё удобство использования, эти программы плохо решают важный практический вопрос. Дело в том, что в обозримом историческом будущем студенты по-прежнему будут вооружены линейкой с карандашом, и, даже располагая качественным «машинным» чертежом, многие не смогут корректно перенести его на клетчатую бумагу. Поэтому в методичке особое внимание уделено технике ручного построения, и значительная часть иллюстраций страницы представляет собой handmade-продукт.

Чем отличается этот справочный материал от аналогов?

Обладая приличным практическим опытом, я очень хорошо знаю, с какими поверхностями чаще всего приходится иметь дело в реальных задачах высшей математики, и надеюсь, что эта статья поможет вам в кратчайшие сроки пополнить свой багаж соответствующими знаниями и прикладными навыками, которых в 90-95% случаев должно хватить.

Что нужно уметь на данный момент?

Во-первых, необходимо уметь правильно строить пространственную декартову систему координат (см. начало статьи Графики и свойства функций).

Во-вторых, необходимо уметь откладывать точки в этой системе координат; об этом я достаточно подробно рассказал на уроках Уравнениях прямой в пространстве и Треугольная пирамида.

Далее считаем, что все события происходят в прямоугольной системе координат.

Что вы приобретёте после прочтения этой статьи?

~~Бутылку~~ После освоения материалов урока вы научитесь быстро определять тип поверхности по её функции и/или уравнению, представлять, как она расположена в пространстве, и, конечно же, выполнять чертежи. Ничего страшного, если не всё уложится в голове с 1-го прочтения – к любому параграфу по мере надобности всегда можно вернуться позже.

Информация по силам каждому – для её освоения не нужно каких-то сверхзнаний, особого художественного таланта и пространственного зрения.

На практике пространственная поверхность обычно задаётся функцией двух переменных или уравнением вида (константа правой части чаще всего равна нулю либо единице). Первое обозначение больше характерно для математического анализа, второе – для аналитической геометрии. Уравнение , по существу, является неявно заданной функцией 2 переменных, которую в типовых случаях легко привести к виду . Напоминаю простейший пример c первого урока по теме ФНП:

– уравнение плоскости вида .

– функция плоскости в явном виде .

Давайте с неё и начнём:

Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Распространенные уравнения плоскостей

Типовые варианты расположения плоскостей в прямоугольной системе координат детально рассмотрены в самом начале статьи Уравнение плоскости. Тем не менее, ещё раз остановимся на уравнениях, которые имеют огромное значение для практики.

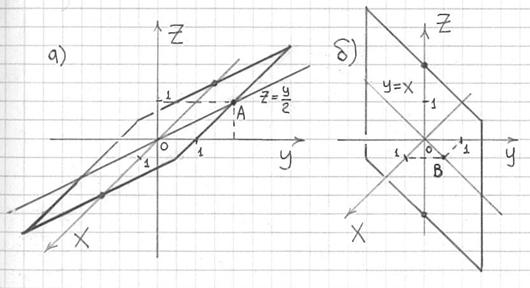
Прежде всего, вы должны на полном автомате узнавать уравнения плоскостей, которые параллельны координатным плоскостям . Фрагменты плоскостей стандартно изображают прямоугольниками, которые в последних двух случаях выглядят, как параллелограммы. По умолчанию размеры можно выбрать любые (в разумных пределах, конечно), при этом желательно, чтобы точка, в которой координатная ось «протыкает» плоскость являлась центром симметрии:

Строго говоря, координатные оси местами следовало изобразить пунктиром, но во избежание путаницы будем пренебрегать данным нюансом.

Тем, кто ещё не успел, настоятельно рекомендую ознакомиться с указанной выше статьёй и понять неформальный смысл этих уравнений. Повторим заодно и соответствующие неравенства:

– (левый чертёж) неравенство задаёт дальнее от нас полупространство, исключая саму плоскость ;

– (средний чертёж) неравенство задаёт правое полупространство, включая плоскость ;

– (правый чертёж) двойное неравенство задаёт «слой», расположенный между плоскостями , включая обе плоскости.

Для самостоятельной разминки:

Изобразить тело, ограниченное плоскостями
Составить систему неравенств, определяющих данное тело.

Из-под грифеля вашего карандаша должен выйти старый знакомый прямоугольный параллелепипед. Не забывайте, что невидимые рёбра и грани нужно прочертить пунктиром. Готовый чертёж в конце урока.

Пожалуйста, НЕ ПРЕНЕБРЕГАЙТЕ учебными задачами, даже если они кажутся слишком простыми. А то может статься, раз пропустили, два пропустили, а затем потратили битый час, вымучивая трёхмерный чертёж в каком-нибудь реальном примере. Кроме того, механическая работа поможет гораздо эффективнее усвоить материал и развить интеллект! Не случайно в детском саду и начальной школе детей загружают рисованием, лепкой, конструкторами и другими заданиями на мелкую моторику пальцев. Простите за отступление, не пропадать же двум моим тетрадям по возрастной психологии =)

Следующую группу плоскостей условно назовём «прямыми пропорциональностями» – это плоскости, проходящие через координатные оси:

1) уравнение вида (здесь и далее ) задаёт плоскость, проходящую через ось ;

2) уравнение вида задаёт плоскость, проходящую через ось ;

3) уравнение вида задаёт плоскость, проходящую через ось .

Хотя формальный признак очевиден (какая переменная отсутствует в уравнении – через ту ось и проходит плоскость), всегда полезно понимать суть происходящих событий:

Построить плоскость

Как лучше осуществить построение? Предлагаю следующий алгоритм:

Сначала перепишем уравнение в виде , из которого хорошо видно, что «игрек» может принимать любые значения. Зафиксируем значение , то есть, будем рассматривать координатную плоскость . Уравнения задают пространственную прямую, лежащую в данной координатной плоскости. Изобразим эту линию на чертеже. Прямая проходит через начало координат, поэтому для её построения достаточно найти одну точку. Пусть . Откладываем точку и проводим прямую.

Теперь возвращаемся к уравнению плоскости . Поскольку «игрек» принимает любые значения, то построенная в плоскости прямая непрерывно «тиражируется» влево и вправо. Именно так и образуется наша плоскость , проходящая через ось . Чтобы завершить чертёж, слева и справа от прямой откладываем две параллельные линии и поперечными горизонтальными отрезками «замыкаем» символический параллелограмм:

Так как условие не накладывало дополнительных ограничений, то фрагмент плоскости можно было изобразить чуть меньших или чуть бОльших размеров.

Ещё раз повторим смысл пространственного линейного неравенства на примере . Как определить полупространство, которое оно задаёт? Берём какую-нибудь точку, не принадлежащую плоскости , например, точку из ближнего к нам полупространства и подставляем её координаты в неравенство:

Получено верное неравенство, значит, неравенство задаёт нижнее (относительно плоскости ) полупространство, при этом сама плоскость не входит в решение.

Построить плоскости
а) ;
б) .

Это задания для самостоятельного построения, в случае затруднений используйте аналогичные рассуждения. Краткие указания и чертежи в конце урока.

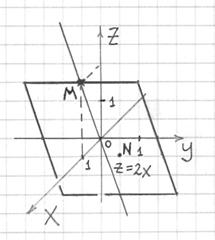
На практике особенно распространены плоскости, параллельные оси . Частный случай, когда плоскость проходит через ось, только что был в пункте «бэ», и сейчас мы разберём более общую задачу:

Построить плоскость

Решение: в уравнение в явном виде не участвует переменная «зет», а значит, плоскость параллельна оси аппликат. Применим ту же технику, что и в предыдущих примерах.

Перепишем уравнение плоскости в виде из которого понятно, что «зет» может принимать любые значения. Зафиксируем и в «родной» плоскости начертим обычную «плоскую» прямую . Для её построения удобно взять опорные точки .

Поскольку «зет» принимает все значения, то построенная прямая непрерывно «размножается» вверх и вниз, образуя тем самым искомую плоскость . Аккуратно оформляем параллелограмм разумной величины:

Готово.

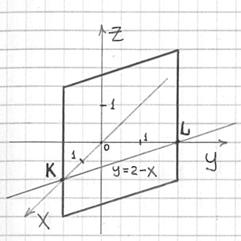
Уравнение плоскости в отрезках

Важнейшая прикладная разновидность. Если все коэффициенты общего уравнения плоскости отличны от нуля, то оно представимо в виде , который называется уравнением плоскости в отрезках. Очевидно, что плоскость пересекает координатные оси в точках , и большое преимущество такого уравнения состоит в лёгкости построения чертежа:

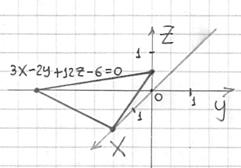
Построить плоскость

Решение: сначала составим уравнение плоскости в отрезках. Перебросим свободный член направо и разделим обе части на 12:

Делаем дроби трёхэтажными:

Именно так! – ведь знаменатели могут оказаться и дробными. Но в данном случае всё разделилось нацело:

Таким образом, плоскость проходит через точки . В целях самоконтроля координаты каждой точки устно подставим в исходное уравнение . После чего выполним чертёж:

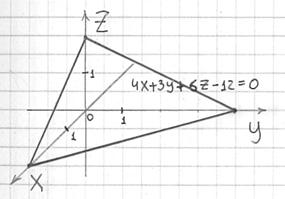
В отличие от предыдущих примеров здесь фрагмент плоскости изображается в виде треугольника, который в общем случае может «прорисоваться» в любом из восьми октантов.

Задание для тренировки:

Построить плоскость

Краткое решение и чертёж в конце урока.

Переходим к другой обширной группе обитателей 3D-мира:

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Цилиндрические поверхности

Или, если короче – цилиндры.

! Примечание: в ряде источников информации под цилиндром понимается исключительно геометрическое тело, а не поверхность!

Следует отметить, что в математике под этими терминами скрывается не совсем то, что обычно подразумевает обыватель, и класс цилиндрических поверхностей не ограничивается чёрным цилиндром на голове:

Построить поверхность, заданную уравнением

…что за дела? Не опечатка ли здесь? Вроде как дано каноническое уравнение эллипса…

Нет, здесь не опечатка и все дела происходят именно в пространстве! Исследуем предложенную поверхность тем же методом, что недавно использовали для плоскостей. Перепишем уравнение в виде , из которого следует, что «зет» принимает любые значения. Зафиксируем и построим в плоскости эллипс . Так как «зет» принимает все значения, то построенный эллипс непрерывно «тиражируется» вверх и вниз. Легко понять, что поверхность бесконечна:

Данная поверхность называется эллиптическим цилиндром. Эллипс (на любой высоте) называется направляющей цилиндра, а параллельные прямые, проходящие через каждую точку эллипса называются образующими цилиндра (которые в прямом смысле слова его и образуют). Ось является осью симметрии поверхности (но не её частью!).

Координаты любой точки, принадлежащей данной поверхности, обязательно удовлетворяют уравнению .

Пространственное неравенство задаёт «внутренность» бесконечной «трубы», включая саму цилиндрическую поверхность, и, соответственно, противоположное неравенство определяет множество точек вне цилиндра.

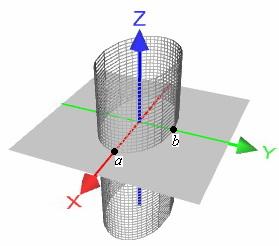
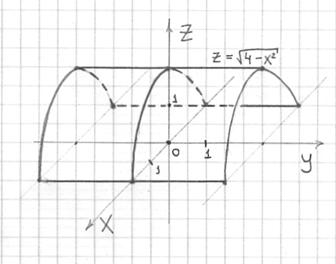
В практических задачах наиболее популярен частный случай, когда направляющей цилиндра является окружность:

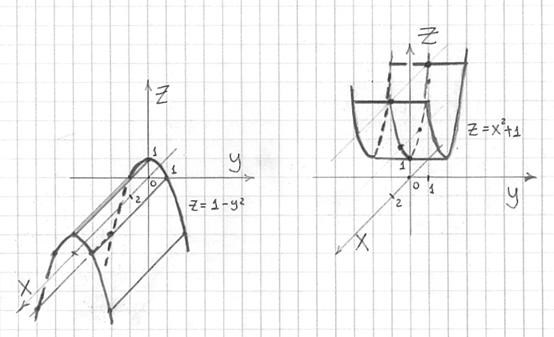
Построить поверхность, заданную уравнением

Бесконечную «трубу» изобразить невозможно, поэтому художества ограничиваются, как правило, «обрезком».

Сначала удобно построить окружность радиуса в плоскости , а затем ещё пару окружностей сверху и снизу. Полученные окружности (направляющие цилиндра) аккуратно соединяем четырьмя параллельными прямыми (образующими цилиндра):

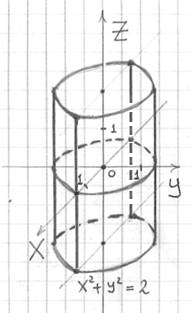
Не забываем использовать пунктир для невидимых нам линий.

Координаты любой точки, принадлежащей данному цилиндру, удовлетворяют уравнению . Координаты любой точки, лежащей строго внутри «трубы», удовлетворяют неравенству , а неравенство задаёт множество точек внешней части. Для лучшего понимания рекомендую рассмотреть несколько конкретных точек пространства и убедиться в этом самостоятельно.

Построить поверхность и найти её проекцию на плоскость

Перепишем уравнение в виде из которого следует, что «икс» принимает любые значения. Зафиксируем и в плоскости изобразим окружность – с центром в начале координат, единичного радиуса. Так как «икс» непрерывно принимает все значения, то построенная окружность порождает круглый цилиндр с осью симметрии . Рисуем ещё одну окружность (направляющую цилиндра) и аккуратно соединяем их прямыми (образующими цилиндра). Местами получились накладки, но что делать, такой уж наклон:

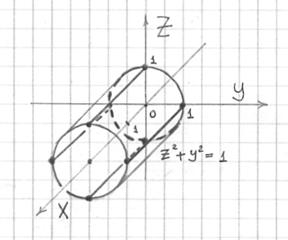
На этот раз я ограничился кусочком цилиндра на промежутке и это не случайно. На практике зачастую и требуется изобразить лишь небольшой фрагмент поверхности.

Тут, к слову, получилось 6 образующих – две дополнительные прямые «закрывают» поверхность с левого верхнего и правого нижнего углов.

Теперь разбираемся с проекцией цилиндра на плоскость . Многие читатели понимают, что такое проекция, но, тем не менее, проведём очередную физкульт-пятиминутку. Пожалуйста, встаньте и склоните голову над чертежом так, чтобы остриё оси смотрело перпендикулярно вам в лоб. То, чем с этого ракурса кажется цилиндр – и есть его проекция на плоскость . А кажется он бесконечной полосой, заключенным между прямыми , включая сами прямые. Данная проекция – это в точности область определения функций (верхний «жёлоб» цилиндра), (нижний «жёлоб»).

Давайте, кстати, проясним ситуацию и с проекциями на другие координатные плоскости. Пусть лучи солнца светят на цилиндр со стороны острия и вдоль оси . Тенью (проекцией) цилиндра на плоскость является аналогичная бесконечная полоса – часть плоскости , ограниченная прямыми ( – любое), включая сами прямые.

А вот проекция на плоскость несколько иная. Если смотреть на цилиндр из острия оси , то он спроецируется в окружность единичного радиуса , с которой мы начинали построение.

Построить поверхность и найти её проекции на координатные плоскости

Это задача для самостоятельного решения. Если условие не очень понятно, возведите обе части в квадрат и проанализируйте результат; выясните, какую именно часть цилиндра задаёт функция . Используйте методику построения, неоднократно применявшуюся выше. Краткое решение, чертёж и комментарии в конце урока.

Эллиптические и другие цилиндрические поверхности могут быть смещены относительно координатных осей, например:

(по знакомым мотивам статьи о линиях 2-го порядка) – цилиндр единичного радиуса с линией симметрии, проходящей через точку параллельно оси . Однако на практике подобные цилиндры попадаются довольно редко, и совсем уж невероятно встретить «косую» относительно координатных осей цилиндрическую поверхность.

Параболические цилиндры

Как следует из названия, направляющей такого цилиндра является парабола.

Построить поверхность и найти её проекции на координатные плоскости.

Не мог удержаться от этого примера =)

Решение: идём проторенной тропой. Перепишем уравнение в виде , из которого следует, что «зет» может принимать любые значения. Зафиксируем и построим обычную параболу на плоскости , предварительно отметив тривиальные опорные точки . Поскольку «зет» принимает все значения, то построенная парабола непрерывно «тиражируется» вверх и вниз до бесконечности. Откладываем такую же параболу, скажем, на высоте (в плоскости) и аккуратно соединяем их параллельными прямыми (образующими цилиндра):

Напоминаю полезный технический приём: если изначально нет уверенности в качестве чертежа, то линии сначала лучше прочертить тонко-тонко карандашом. Затем оцениваем качество эскиза, выясняем участки, где поверхность скрыта от наших глаз, и только потом придаём нажим грифелю.

1) Проекцией цилиндра на плоскость является парабола . Следует отметить, что в данном случае нельзя рассуждать об области определения функции двух переменных – по той причине, что уравнение цилиндра не приводимо к функциональному виду .

2) Проекция цилиндра на плоскость представляет собой полуплоскость , включая ось

3) И, наконец, проекцией цилиндра на плоскость является вся плоскость .

Построить параболические цилиндры:

а) , ограничиться фрагментом поверхности в ближнем полупространстве;

б) на промежутке

В случае затруднений не спешим и рассуждаем по аналогии с предыдущими примерами, благо, технология досконально отработана. Не критично, если поверхности будут получаться немного корявыми – важно правильно отобразить принципиальную картину. Я и сам особо не заморачиваюсь над красотой линий, если получился сносный чертёж «на троечку», обычно не переделываю. В образце решения, кстати, использован ещё один приём, позволяющий улучшить качество чертежа 😉

Гиперболические цилиндры

Направляющими таких цилиндров являются гиперболы. Этот тип поверхностей, по моим наблюдениям, встречается значительно реже, чем предыдущие виды, поэтому я ограничусь единственным схематическим чертежом гиперболического цилиндра :

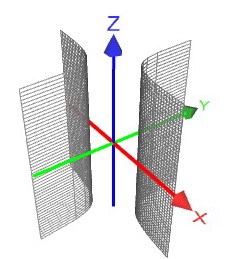
Принцип рассуждения здесь точно такой же – обычная школьная гипербола из плоскости непрерывно «размножается» вверх и вниз до бесконечности.

Рассмотренные цилиндры относятся к так называемым поверхностям 2-го порядка, и сейчас мы продолжим знакомиться с другими представителями этой группы:

Видео:§65 ЭллипсоидСкачать

Эллипсоид. Сфера и шар

Каноническое уравнение эллипсоида в прямоугольной системе координат имеет вид , где – положительные числа (полуоси эллипсоида), которые в общем случае различны. Эллипсоидом называют как поверхность, так и тело, ограниченное данной поверхностью. Тело, как многие догадались, задаётся неравенством и координаты любой внутренней точки (а также любой точки поверхности) обязательно удовлетворяют этому неравенству. Конструкция симметрична относительно координатных осей и координатных плоскостей:

Происхождение термина «эллипсоид» тоже очевидно: если поверхность «разрезать» координатными плоскостями, то в сечениях получатся три различных (в общем случае) эллипса. В зависимости от значений эллипсоид может быть вытянут вдоль любой оси, причём вытянут достаточно далеко.

Если две полуоси совпадают, то данную поверхность/тело называют эллипсоидом вращения. Так, например, эллипсоид получен вращением эллипса вокруг оси (представьте мысленно).

Небольшая задачка для самостоятельного решения:

Построить эллипсоид . Записать уравнение порождающего эллипса и ось, вокруг которой осуществляется его вращение.

Чертёж и краткий комментарий в конце урока.

В случае равенства всех полуосей , эллипсоид вырождается в сферу:
– данное уравнение задаёт сферу с центром в начале координат радиуса .

Тело, ограниченное сферой, называется шаром. Неравенство определяет шар с центром в начале координат радиуса . И, соответственно, противоположному условию удовлетворяют координаты любой внешней точки.

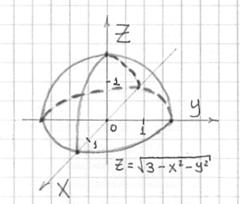
Разделаемся с аппетитным Колобком:

Построить поверхность . Найти функции, задающие верхнюю и нижнюю полусферу, указать их области определения. Записать аналитическое выражение шара, ограниченного данной сферой и проверить, принадлежат ли ему точки

Решение: уравнение задаёт сферу с центром в начале координат радиуса 2. Здесь, как и в примерах с параболическими цилиндрами, выгодно уменьшить масштаб чертежа:

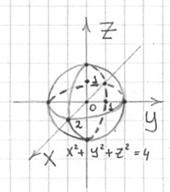
Выразим «зет»:

– функция, задающая верхнюю полусферу;
– функция, задающая нижнюю полусферу.

Областью определения каждой функции является круг с центром в начале координат радиуса 2 (проекция полусфер на плоскость ).

Неравенство определяет шар с центром в начале координат радиуса 2. Подставим координаты точек в данное неравенство:

Получено неверное неравенство, следовательно, точка «дэ» лежит вне шара.

Получено верное неравенство, значит, точка «эф» принадлежит шару, а конкретнее – его границе (сфере).

Материал о сферах и шарах достаточно прост, и я предлагаю вам чисто символическое задание для самостоятельного решения:

Найти область определения функции двух переменных и построить соответствующую поверхность.

Краткое решение и чертёж в конце урока.

Кстати, наша планета, кто не знает, чуть-чуть, но таки не шар.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

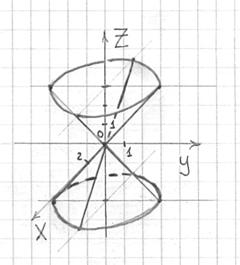
Коническая поверхность

Каноническое уравнение в декартовых координатах задаёт коническую поверхность 2-го порядка или, если короче, конус. Но это опять же не совсем тот конический колпак, который всем знаком со времён далёкого детства.

Форму многих поверхностей удобно исследовать методом сечений, который я потихоньку начал использовать ещё в предыдущих параграфах. Суть метода состоит в том, что мы «рассекаем пациентов» плоскостями (прежде всего, координатными), и получившиеся сечения позволяют нам хорошо понять, как выглядит та или иная поверхность.

Перепишем уравнение в виде и исследуем сечения конуса плоскостями , параллельными плоскости . Подставим в уравнение конической поверхности:

Очевидно, что случаю соответствует уравнение , задающее пару мнимых пересекающихся прямых с единственной действительной точкой пересечения в начале координат. Данная точка называется вершиной конуса.

Если же , то уравнение задаёт эллипсы различных размеров, причём из последнего уравнения хорошо видно, что с увеличением абсолютных значений «цэ большого» полуоси эллипсов неограниченно возрастают. Таким образом, коническая поверхность бесконечна:

Если коническую поверхность «разрезать» произвольной плоскостью (которая проходит через ось ), то в сечении получатся две пересекающиеся в начале координат прямые. Множество таких сечений, собственно, и образует коническую поверхность.
И логично, что каждая из этих прямых называется образующей конуса.

На практике почти всегда приходится иметь дело с конусом вращения, в котором сечения плоскостями представляют собой окружности. И во многих практических задачах типичен следующий «опознавательный» вид уравнения:
– с «зет» в левой части и равными коэффициентами при и .

Как многие догадались, функция задаёт верхнюю часть конуса, а функция – его нижнюю часть.

Распространённая вариация по теме:

Построить поверхность

Решение: уравнение имеет вид и определяет половину конуса, располагающуюся в верхнем полупространстве. Вершина конической поверхности, понятно, расположена в начале координат, но как построить всё остальное?

Возведём обе части исходного уравнения в квадрат:

Далее выберем небольшое положительное значение «зет», например , и найдём линию пересечения этой плоскости с нашей поверхностью:
– окружность радиуса .

Пояснение на всякий случай: подставили в 1-е уравнение

Теперь на высоте изобразим окружность и аккуратно проведём 4 образующие конуса:

Образующие, в принципе, можно было продолжить и выше плоскости .

Не забываем, что уравнение задаёт только верхнюю часть поверхности и поэтому никаких «хвостиков» в нижнем полупространстве быть не должно.

Пожалуй, простейшая коническая поверхность:

Построить коническую поверхность . Записать неравенства, определяющие внутреннюю и внешнюю часть конуса.

В образце решения изображён фрагмент конуса, расположенный между плоскостями . Ну, а с неравенствами, думаю, сообразите самостоятельно. В случае мучительных сомнений всегда можно взять точку (внутри или снаружи конуса) и проверить, удовлетворяют ли её координаты неравенству.

В заключение статьи подробно рассмотрим ещё одну мегапопулярную поверхность:

Видео:ЭллипсСкачать

Эллиптический параболоид

Каноничный эллиптический параболоид в прямоугольной системе задаётся уравнением . Данная поверхность выглядит бесконечной чашей:

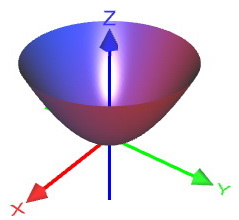
Название «эллиптический параболоид» тоже произошло из результатов исследования сечений. В горизонтальных сечениях плоскостями получаются различные эллипсы:
, в частности, при эллипс вырождается в точку (начало координат), которая называется вершиной эллиптического параболоида.

А вертикальные сечения плоскостями, параллельными оси , представляют собой различные параболы. Например, сечение координатной плоскостью :
– парабола, лежащая в плоскости .
Или сечение плоскостью :
– парабола, лежащая в плоскости .

Отсюда и эллиптический параболоид.

На практике обычно встречается упрощенная версия поверхности с горизонтальными сечениями-окружностями. Перепишем каноническое уравнение в прикладном функциональном виде:
– характерным признаком функции, как и в ситуации с конусом, является равенство коэффициентов при .

Построить поверхность . Записать неравенства, определяющие внутреннюю и внешнюю часть эллиптического параболоида.

Решение: используем ту же методику, что и при построении конической поверхности. Рассмотрим какое-нибудь не очень большое значение «зет», здесь удобно выбрать , и найдём сечение эллиптического параболоида этой плоскостью:
– окружность радиуса 2.

Теперь на высоте изобразим данную окружность и аккуратно соединим её с вершиной (началом координат) двумя параболами. В результате получится такая вот симпатичная чашка:

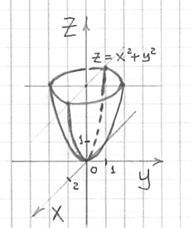
Рассматриваемый частный случай параболоида с горизонтальными сечениями-окружностями также называют параболоидом вращения, поскольку его можно получить вращением параболы вокруг оси

С неравенствами ничего нового. Нетрудно догадаться, что неравенство или, если развернуть запись в более привычном порядке, определяет множество точек внутри чаши (т.к. неравенство строгое, то сама поверхность не входит в решение). И, соответственно, неравенство задаёт множество внешних точек.

По моим наблюдениям, на практике часто встречается эллиптический параболоид вида , который выглядит точно так же, но мигрировал вершиной в точку . Именно такую поверхность мы исследовали с помощью линий уровня в Примере № 14 первого урока темы.

Ещё одно типичное расположение эллиптического параболоида:

Построить поверхность

Решение: если коэффициенты при отрицательны (сразу оба), то чаша параболоида «смотрит вниз». Вершина поверхности расположена в точке . Это понятно не только интуитивно, но и подкрепляется простым аналитическим рассуждением: очевидно, что рассмотрев любую другую пару значений мы уменьшим функцию . Таким образом, в точке достигается максимум функции двух переменных.

В целях построения поверхность удобно «отсечь» плоскостью . Сечение представляет собой:
– окружность радиуса 2.

Выполним чертёж: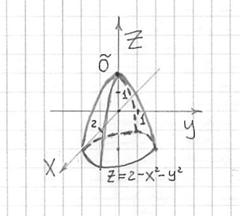

Готово.

Заключительное задание для самостоятельного решения:

Построить эллиптический параболоид

Чертёж в конце урока, который приблизился к своему завершению.

Среди поверхностей 2-го порядка за кадром остались редко встречающиеся на практике:

( ниже перечислены канонические уравнения, в которых – положительные числа)

– гиперболический параболоид («седло»);

– однополостной гиперболоид;

– двуполостной гиперболоид.

Более подробную информацию об этих поверхностях можно почерпнуть в учебнике аналитической геометрии либо другом источнике информации, в частности, в Википедии, на которую проставлены ссылки. Если возникнет необходимость выполнить их построение – используйте метод сечений, он действительно прост и эффективен!

Я бы с радостью всё рассказал, но, во-первых, это нецелесообразно с практической точки зрения, а во-вторых, размер статьи подходит к той опасной грани, после которой посетители сайта будут считать автора не только фанатом, но и начнут всерьёз опасаться за его здоровье. Впрочем, санитары разрешили мне ещё немного посидеть за компьютером =)

А если серьёзно, то этой статьи я опасался чуть ли не с первых дней создания сайта ввиду большого объема работы. Но вот, наконец, клуб любителей функций двух переменных широко распахнул двери, и теперь-то уж мы с вами оттянемся в полный рост =)

Решения и чертежи:

Пример 1: Решение: выполним чертёж: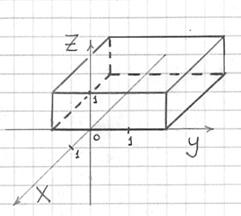

Данное тело определяется системой

Пример 3: Решение: а) Сначала удобно построить прямую , лежащую в плоскости . Используем начало координат, и, например, точку . б) Сначала удобно построить прямую , лежащую в плоскости . Используем начало координат, и, например, точку .

Пример 6: Решение: запишем уравнение плоскости в отрезках:

Выполним чертёж:

Пример 10: Решение: функция задаёт верхнюю часть цилиндра :

Проекция на плоскость : часть данной плоскости, ограниченная «плоскими» прямыми (включая прямые).
Проекция на плоскость : часть данной плоскости, ограниченная прямыми ( – любое), включая сами прямые.
Проекция на плоскость : полуокружность

Пример 12: Чертежи:

Пример 13: Решение: данный эллипсоид получен вращением эллипса (плоскость ) вокруг оси :

Примечание: также можно считать, что вращается эллипс , лежащий в плоскости .

Пример 15: Решение: областью определения данной функции является круг с центром в начале координат радиуса . Функция задаёт полусферу, лежащую в верхнем полупространстве, с центром в начале координат радиуса :

Пример 17: Решение: сечения конуса плоскостями представляют собой окружности . Выполним чертёж:

Неравенство задаёт множество точек, находящихся внутри конуса; неравенство задаёт множество внешних точек.

Пример 20: Решение: вершина параболоида находится в точке . Выполним чертёж:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Видео:Эллипс (часть 1). Каноническое уравнение. Высшая математика.Скачать

Эллипсоиды

Видео:§18 Каноническое уравнение эллипсаСкачать

Определение эллипсоида

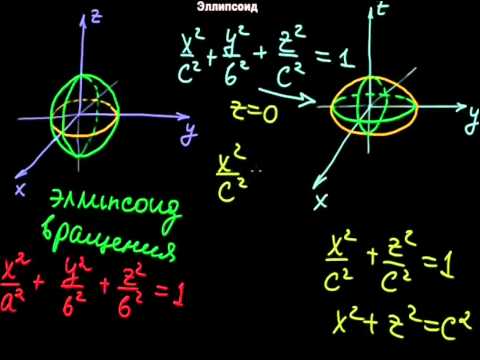
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

где — положительные параметры, удовлетворяющие неравенствам .

Если точка принадлежит эллипсоиду (4.46), то координаты точек при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям , имеют длины соответственно. Если b>c» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAQBAMAAACcpY7MAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAEacB0WkhgcA75ZFRKK9ZmAAAARhJREFUKM9jYKAEJHUQq1L0igGRKhlv45dXg7N47oAppgRcruuE2cl9EUyxaUxGs2vHtgCI0h6oUhPXpgkQpYdhiiKaBBgYZgWfvQw11RWiVPaq6UKIqSrBEBkRNakNDIyLGLicoTrFIUrPBnBehdpXAlbK6GJQW8DAfodBdgPMEvHlIHKvgOV1mNOqCkAOv8MgycBgtZjh7AF4SLqDSBcG9qswlSEglVZg58k2A82A2w5iMV9i4LgGsz0QRNk2gMkCBi8msFcZ0l2ZQe5kvs6QqwDxUUmAMVgNkJvAwKLAekkExevM2gwqAiheN3JgEApg4FytuksHNeRn7VJEDXnGjiJNkIABGyjaGDURkTERTApNQMQOUAQACxo8dxA2UAQAAAAASUVORK5CYII=» />, то число называется большой полуосью, число — средней полуосью, число — малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям , то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств .

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Плоские сечения эллипсоида

Подставляя в уравнение (4.46), получаем уравнение линии пересечения эллипсоида с координатной плоскостью . Это уравнение в плоскости определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.

Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.46), получаем

При c» png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость не пересекает эллипсоид. При уравнение (4.47) имеет нулевое решение . Следовательно, плоскости касаются эллипсоида в его вершинах . При , разделив обе части уравнения (4.47) на 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGMAAAAwBAMAAAD3D9n/AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAmv2BWBABQTDA2LEhcNbL+n8AAAGvSURBVEjHY2CgJughWUeg9VRStQgyrCZVixCDFAmqWcvB1G4StDhpgUgODVJsUQSRUQ0kaGFRAenbwUKCFkYdIMHtXkiClqxlxwMYhJQUSdASNFtag6G9vIaUEFvKpkhqLDawKpOmg21VAjjMSIsWRlXStACtSNrgSpIWYLQ4uS0jSQvnAganQgd8KngC0AQSHRiYp2BXGw5OdxlGBeghlobLdObFO4Hms2lOKiA69J0CGEF+TDAioIXlKpy5moEdHGGEtKR5mUJZHMrQrERIC1ualwzUPmWgP4jRwsDGVgnRwwzSkkCMFiCo3A7TooSwxdkYBEDBHigIB8JwPYUzoFq0EojVcnAGzC9EO2w6SGWGMgOPNlHeZ4B5n00bGi9CDoS0wAKZwSiAcSlQp5KS0gRs6i7CI93LBp4tlgg1gGMqAZuOxFYpaApPMUWINuPLeUwXgqAOZksgMtUmNjBdILkaczpAqg7WJaSpb29g4G4gSUfn5I0MEhyk+IVDmU0pcbNlAQlaghaw7T05cyYp3r9EevBOaiBdSwLJWoQSGKJJ1BIl2ruCRC2p1iJ4ZAESoVYyhvDZkwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, получаем уравнение эллипса полуосями . Следовательно, сечение эллипсоида плоскостью при представляет собой эллипс.

Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Эллипсоиды вращения

Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом ). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при являются окружностями. Следовательно, сечения эллипсоида плоскостями представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси эллипс заданный в плоскости (рис.4.41,а).

Если , то все сечения эллипсоида (4.46) плоскостями при эллипс (рис.4.41,б).

Если все полуоси эллипсоида равны , то он представляет собой сферу радиуса , которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.

Эллипсоид, у которого полуоси попарно различны b>c)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAGAAAAAWBAMAAADNzYTXAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAXynYREhwNFB6DGRUQyCkmkAAAGUSURBVDjLY2AgHbBcIFYlkwOYcsYm51yCTRQsyLYUm9T2t9hEoxKABLsCNimep9hEmQ2AxL4AhG8c4EyJRjDlIoCige0ZkDiBJOahCmPFHYAY0RSArIFxEZCoAWJO49sJYAG4jnvKRWBaBK6D29ySgcEYqOYRkGO1tQ7iE0YPM4j0ubYoiIhIcwJEROuilgADEDE+AVr8ksEPFhnTwToYuwLYF0IEJIvBOljeMr5iYNQTYGB9CQytBoZzCTBnTrcGkqxvGNgfMsB0bACSeY0M2xgY/CAa/BQYuuAem1wNJHjfMsgtgApwmoM06IFd6Adx0rkJrI9h6qdbghPBM4Z5BlD1xRNAlB2YBDoJ5Gm9AN4nyRAHXYd4WughzJGyEC+AlLIxMGpBgvVeQsRLFUhEQAOJ+yn3E0hEwAJp3gVGjQAGcyBLQ4CBp8dycQFqxJ2wuIAacSxrjitAIi4PKBTKIAl2OVw9A+tGMKWEiGhpoAjbayBDWIH4rMMDcgfnUuI1gJM39gyEFTCaQDIe0VkUKfkTDwAVFViuYeRgnwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, называется трехосным (или общим).

1. Плоскости определяют в пространстве основной прямоугольный параллелепипед , внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.

2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.

3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.

В самом деле, если точка принадлежит эллипсоиду, то точки с координатами при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).