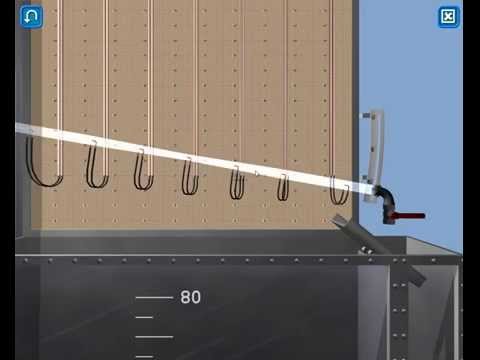
Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.
Что такое идеальная жидкость?
Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.
Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

ПАХТ 4. Лабораторная работа 4 Экспериментальная демонстрация уравнения Бернулли студент группы 419144 Шакиров Б. Р. Проверил
| Название | Лабораторная работа 4 Экспериментальная демонстрация уравнения Бернулли студент группы 419144 Шакиров Б. Р. Проверил |
| Дата | 14.04.2021 |
| Размер | 55.24 Kb. |
| Формат файла |  |
| Имя файла | ПАХТ 4.docx |
| Тип | Лабораторная работа #194624 |
| Подборка по базе: Контрольная работа Материаловедение.docx, ПРАКТИЧЕСКАЯ РАБОТА №1 Конституционное право Ч.1 (ТЕКСТ ЗАДАНИЯ , Самостоятельная работа по теме 1.5..docx, ПИСЬМЕННАЯ РАБОТА №1 БЖД.pdf, Практическая работаТеория вероятностей и математическая статисти, Контрольная работа.docx, Самостоятельная работа по теме 1.3.docx, Информатика лабораторная 1 Вариант 8.docx, Конт работа.docx, Метод_указания к Лабораторным работам (1).doc Министерство высшего образования и науки РФ «Казанский национальный исследовательский технологический университет» Кафедра «Процессы и аппараты химической технологии» («ПАХТ») Лабораторная работа №4 «Экспериментальная демонстрация уравнения Бернулли» студент группы 4191-44 доцент кафедры ПАХТ Казань 2021 1) уяснение физического смысла уравнения Бернулли; 2) определение потерь напора в трубопроводе переменного сечения; 3) ознакомление со способами измерения средней и локальной скоростей движения жидкости. Описание и схема установки: Рис.1. Схема установки 1 – напорный бак, 2 – трубопровод переменного сечения, 3 – мерный бак, 4 – сливной отсек мерного бака, 5, 7, 9 – вентиль, 6 – кран, 8 – патрубок, 10 – пьезометрическая трубка, 11 – трубка Пито 1.Что называется напором? В гидравлике энергия, отнесенная к единице веса жидкости, называется напором и измеряется высотой столба жидкости. 2.В чем заключается смысл уравнения Бернулли? где w – скорость в рассматриваемом сечении элементарной струйки, м/с; р – давление в том же сечении, Па ; z – геометрическая высота 49 расположения этого сечения относительно произвольно выбранной горизонтальной плоскости сравнения О – О, м; ρ – плотность жидкости, кг/м 3 ; g – ускорение силы тяжести, м/с 2 В уравнении Бернулли 3.Как определяют полный и статический напоры? Сумма геометрического и пьезометрического напоров называется статическим напором Полный гидродинамический напор – это сумма геометрического, пьезометрического и скоростного напоров 4.Что представляет собой потерянный напор? Потерянный напор∆hi—j – это та удельная (отнесенная к единице веса) механическая энергия, которая перешла в теплоту при движении жидкости между сечениями i и j трубы? В каком случае потерянный напор можно было бы определить по показаниям пьезометрических трубок? 6.Как измеряется скоростной напор? Какой скорости соответствует полученный таким способом скоростной напор? Трубка Пито и пьезометрическая трубка должны быть установлены так, чтобы центры сечений на входе в эти трубки лежали в исследуемом сечении трубопровода. По разности уровней в них определяют скоростной напор и соответственно местную скорость в точке потока, совпадающей с центром сечения входа в трубку Пито: По величине скоростного напора для каждого сечения вычисляется местная скорость движения жидкости 7.Как определяются средняя и местная скорости течения жидкости? Величина средней скорости в сечениях определяется из уравнения расхода: Где расход По величине скоростного напора для каждого сечения вычисляется местная скорость движения жидкости 8.Что представляет собой диаграмма Бернулли? Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора. Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты z оси трубопровода. 9.Как строится линия полного напора? Линия полного напора идеальной жидкости проводится параллельно оси абсцисс на расстоянии (hпз1+z1) от плоскости сравнения. За счет потерь на трение линия полного напора вязкой жидкости на каждом прямом участке трубы должна иметь некоторый уклон в сторону течения жидкости. Однако на данной экспериментальной установке эти потери очень малы. Поэтому на каждом участке через точки полных напоров в данных сечениях проводятся условно с небольшим наклоном линии полного напора до границ сужений а, b, c. Затем точки пересечения линий полных напоров с границами сужений соединяют отрезками прямых. В сужениях между отдельными участками проис- 55 ходит деформация потока, что приводит к вихреобразованию и к более резкому падению полного напора, чем на прямых участках трубопровода. 10.Как строится линия статического напора? Линия статического напора на прямых участках проводится параллельно соответствующим линиям полного напора, поскольку на прямых участках скорость потока (и скоростные напоры) не изменяется. Как это следует из уравнения Бернулли, в сужениях происходит сначала резкое уменьшение, а затем возрастание статического напора. Так как в местах сужений не осуществляются измерения напоров, линия статического напора в сечениях а, b, c проводится произвольно 11.Как по диаграмме Бернулли определить потерянный напор? Вычесть из значения полного напора в начальном сечении значение полного напора в конечном сечении рассматриваемых участков 12.Приведите примеры и дайте объяснение использованию уравнения Бернулли в технике Уравнение Бернулли широко применяется в технике, как для выполнения гидравлических расчетов, так и для решения ряда практических задач. Одной из таких задач является измерение скорости и расхода жидкости. Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе. Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. На этом же принципе основано измерение скорости полета самолета. Запишем уравнение Бернулли для струйки, которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где υ = 0), получаем Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0, следовательно из предыдущего имеем Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха . Поток воздуха; засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха. Найдем соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) ζв и жиклера ζж (сопротивлением бензотрубки пренебрегаем). З Учитывая, что массовые расходы Обработка экспериментальных данных t = 124 сек V=28
D1=27мм Видео:Закон БернуллиСкачать  Диаграмма уравнения БернуллиГидростатика и гидродинамика Отчет по лабораторным работам Выполнил: студент гр.64301 Проверил: Перский С.Н. Лабораторная работа №1 Тема:”Определение гидростатического давления” Цель: “Освоение способов измерения гидростатического давления” hв— вакуумметрическая высота; g – ускорение свободного падения; ρ – плотность жидкости. Таблица 1: Показания пьезометра П 1 и механического прибора МН 1 Жидкость: Масло ВМГЗ плотность ρ1=860 кг/м 3
Таблица 2. Показания батарейного мановакуумметра и механического прибора Жидкость: Масло гидравлическое Плотность: 860 кг/м 3
g – ускорение свободного падения. Таблица 3. Показания U – образного мановакуумметра и механических приборов.
ЛАБОРАТОРНАЯ РАБОТА №3 Тема:Определение силы давления жидкости на плоские стенки. Цель работы:демонстрация закона Паскаля, приобретение навыков определения силы избыточного давления на плоские горизонтальную и вертикальную стенки.
|




















 =hск – скоростной напор; p/ρg = hпз – пьезометрический напор; z – геометрический напор. Сумма геометрического и пьезометрического напоров называется статическим напором. Следовательно, уравнение Бернулли можно сформулировать следующим образом: сумма геометрического, пьезометрического и скоростного напоров (полный гидродинамический напор) в любом сечении потока невязкой жидкости есть величина постоянная. Из уравнения Бернулли следует, что увеличение какой-либо составляющей полного гидродинамического напора (например, скоростного напора) приводит к уменьшению другой составляющей (например, пьезометрического напора), и наоборот. Таким образом, уравнение Бернулли является математическим выражением закона сохранения и превращения механической энергии применительно к движущейся идеальной жидкости.
=hск – скоростной напор; p/ρg = hпз – пьезометрический напор; z – геометрический напор. Сумма геометрического и пьезометрического напоров называется статическим напором. Следовательно, уравнение Бернулли можно сформулировать следующим образом: сумма геометрического, пьезометрического и скоростного напоров (полный гидродинамический напор) в любом сечении потока невязкой жидкости есть величина постоянная. Из уравнения Бернулли следует, что увеличение какой-либо составляющей полного гидродинамического напора (например, скоростного напора) приводит к уменьшению другой составляющей (например, пьезометрического напора), и наоборот. Таким образом, уравнение Бернулли является математическим выражением закона сохранения и превращения механической энергии применительно к движущейся идеальной жидкости.




 ;
;  , V- объем воды, равный емкости мерного бака, t- – время заполнения мерного бака
, V- объем воды, равный емкости мерного бака, t- – время заполнения мерного бака

 .
. аписав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):
аписав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):

 и
и  , получим
, получим

 ,
, 






 м
м м
м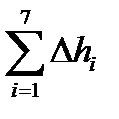
 ,
,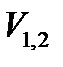 – средняя скорость в соответствующем сечении, см/с;
– средняя скорость в соответствующем сечении, см/с; и
и  – площади живых сечений, см 2 .
– площади живых сечений, см 2 .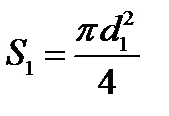 и
и 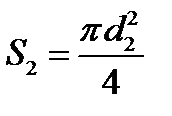
 и
и 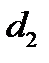 – диаметры сечений трубопровода и узкой части, см.
– диаметры сечений трубопровода и узкой части, см. и
и 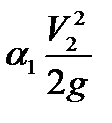 ,
, – коэффициент неравномерности распределения скоростей (кинетический коэффициент Кориолиса) в установленном турбулентном потоке
– коэффициент неравномерности распределения скоростей (кинетический коэффициент Кориолиса) в установленном турбулентном потоке 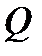 , см 3 /с
, см 3 /с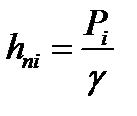
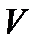 , см/с
, см/с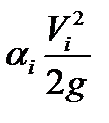 , мм
, мм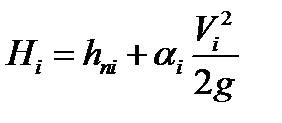

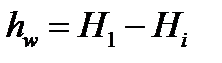 , мм
, мм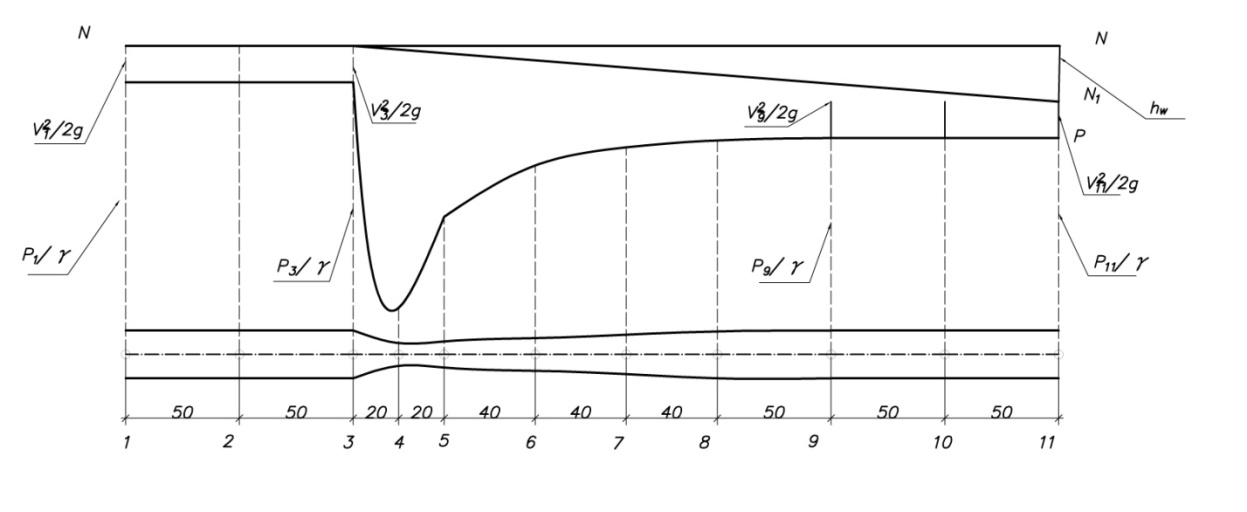
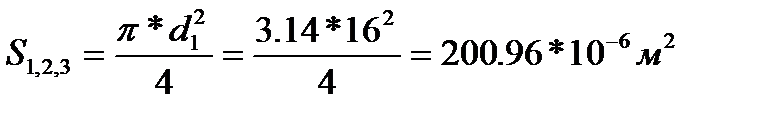


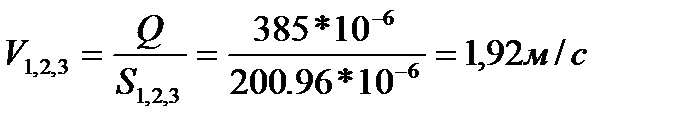


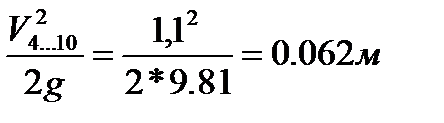
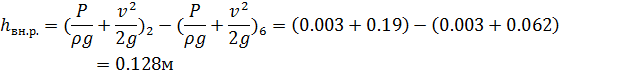
 67
67