Решение уравнений через переход к уравнениям-следствиям может привести к появлению так называемых посторонних корней. В этой статье мы, во-первых, детально разберем, что такое посторонние корни. Во-вторых, поговорим о причинах их возникновения. И в-третьих, на примерах рассмотрим основные способы отсеивания посторонних корней, то есть, проверки корней на предмет наличия среди них посторонних с целью исключения их из ответа.
- Посторонние корни уравнения, определение, примеры
- Причины возможного появления посторонних корней
- Что такое отсеивание посторонних корней?
- Способы отсеивания посторонних корней
- Проверка подстановкой
- По ОДЗ
- По условиям ОДЗ
- Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
- Как решать логарифмические уравнения подробный разбор примеров
- Сложение и вычитание логарифмов.
- Что такое логарифм и как его посчитать
- Два очевидных следствия определения логарифма
- Свойства логарифмов
- Степень можно выносить за знак логарифма
- Логарифм произведения и логарифм частного
- Формула перехода к новому основанию
- Сумма логарифмов. Разница логарифмов
- Логарифмический ноль и логарифмическая единица
- Как решать уравнения с логарифмами: 2 способа с примерами
- Сравнение логарифмов
- Пример Найдите корень уравнения.
- Логарифмы со специальным обозначением
- Десятичный логарифм
- Натуральный логарифм
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Использование свойств логарифмов при решении логарифмических уравнений и неравенств
- math4school.ru
- Ошибки в уравнениях
- Потеря корней
- Посторонние корни
- Ошибки, связанные с заменой переменной
- Ошибки, связанные с использованием модуля
- Подбор корней без обоснования
- Ошибки в логарифмических и показательных уравнениях
- Ошибки в тригонометрических уравнениях
Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Посторонние корни уравнения, определение, примеры
В школьных учебниках по алгебре не дается определение постороннего корня. Там представление о постороннем корне формируется путем описания следующей ситуации: при помощи некоторых преобразований уравнения осуществляется переход от исходного уравнения к уравнению-следствию, находятся корни полученного уравнения-следствия, и осуществляется проверка найденных корней подстановкой в исходное уравнение, которая показывает, что некоторые из найденных корней не являются корнями исходного уравнения, эти корни называют посторонними корнями для исходного уравнения [1, с. 174-175; 2, с. 202; 3, с. 187-188].
Отталкиваясь от этой базы, для себя можно принять такое определение постороннего корня:
Посторонние корни – это корни полученного в результате проведения преобразований уравнения-следствия, не являющиеся корнями исходного уравнения.
Приведем пример. Рассмотрим уравнение 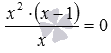
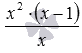
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Причины возможного появления посторонних корней
Если для получения уравнения-следствия не использовать никакие «экзотические» преобразования, а использовать только основные преобразования уравнений, то посторонние корни могут возникнуть лишь по двум причинам:
- из-за расширения ОДЗ и
- из-за возведения обеих частей уравнения в одну и ту же четную степень.
Здесь стоит напомнить, что расширение ОДЗ в результате преобразования уравнения в основном происходит
- При сокращении дробей;
- При замене нулем произведения с одним или несколькими нулевыми множителями;
- При замене нулем дроби с нулевым числителем;
- При использовании некоторых свойств степеней, корней, логарифмов;
- При использовании некоторых тригонометрических формул;
- При умножении обеих частей уравнения на одно и то же выражение, обращающееся в нуль на ОДЗ для этого уравнения;
- При освобождении в процессе решения от знаков логарифмов.
Пример из предыдущего пункта статьи иллюстрирует появление постороннего корня из-за расширения ОДЗ, которое имеет место при переходе от уравнения 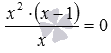
Также приведем пример появления постороннего корня из-за возведения обеих частей уравнения в одну и ту же четную степень. Иррациональное уравнение 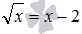
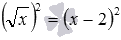
Заметим, что расширение ОДЗ и возведение обеих частей уравнения в одну и ту же четную степень, не всегда приводит к появлению посторонних корней. Например, при переходе от уравнения 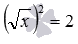
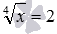
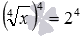
Видео:Логарифмические уравнения. 11 класс.Скачать

Что такое отсеивание посторонних корней?
Термин «отсеивание посторонних корней» лишь с натяжкой можно назвать устоявшимся, он встречается далеко не во всех учебниках алгебры, но является интуитивно понятным, из-за чего обычно и используется. Что понимают под отсеиванием посторонних корней, становится понятно из следующей фразы: «… проверка – обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»)» [1, с.176].
Отсеивание посторонних корней – это обнаружение и отбрасывание посторонних корней.
Теперь можно переходить к способам отсеивания посторонних корней.
Видео:84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Способы отсеивания посторонних корней
Проверка подстановкой
Основной способ отсеивания посторонних корней – это проверка подстановкой. Он позволяет отсеять посторонние корни, которые могли возникнуть и по причине расширения ОДЗ, и по причине возведения обеих частей уравнения в одну и ту же четную степень.
Проверка подстановкой состоит в следующем: найденные корни уравнения-следствия по очереди подставляются в исходное уравнение или в любое равносильное ему уравнение, те из них, которые дают верное числовое равенство, являются корнями исходного уравнения, а те, которые дают неверное числовое равенство или выражение, не имеющее смысла, являются посторонними корнями для исходного уравнения.
Покажем на примере, как проводится отсеивание посторонних корней через подстановку в исходное уравнение.
Решите уравнение
В некоторых случаях отсеивание посторонних корней целесообразнее проводить другими способами. Это относится в основном к тем случаям, когда проверка подстановкой связана со значительными вычислительными трудностями или когда стандартный способ решения уравнений какого-то определенного вида предполагает другой проверки (например, отсеивание посторонних корней при решении дробно-рациональных уравнений проводится по условию не равенства нулю знаменателя дроби). Разберем альтернативные способы отсеивания посторонних корней.
По ОДЗ
В отличие от проверки подстановкой, отсеивание посторонних корней по ОДЗ уместно не всегда. Дело в том, что этот способ позволяет отсеивать лишь посторонние корни, возникающие по причине расширения ОДЗ, и он не гарантирует отсеивание посторонних корней, которые могли возникнуть по другим причинам, например, из-за возведения обеих частей уравнения в одну и ту же четную степень. Более того, не всегда просто отыскать ОДЗ для решаемого уравнения. Тем не менее, способ отсеивания посторонних корней по ОДЗ стоит держать на вооружении, так как часто его использование требует меньших вычислительных работ, чем использование других способов.
Отсеивание посторонних корней по ОДЗ проводится следующим образом: все найденные корни уравнения-следствия проверяются на предмет принадлежности области допустимых значений переменной для исходного уравнения или любого равносильного ему уравнения, те из них, которые принадлежат ОДЗ, являются корнями исходного уравнения, а те из них, которые не принадлежат ОДЗ, являются посторонними корнями для исходного уравнения.
Анализ приведенной информации приводит к выводу, что отсеивание посторонних корней по ОДЗ целесообразно проводить, если единовременно:
- легко находится ОДЗ для исходного уравнения,
- посторонние корни могли возникнуть только по причине расширения ОДЗ,
- проверка подстановкой связана со значительными вычислительными сложностями.
Покажем, как проводится отсеивание посторонних корней, на практике.
Решите логарифмическое уравнение
По условиям ОДЗ
Как мы сказали в предыдущем пункте, если посторонние корни могли возникнуть лишь по причине расширения ОДЗ, то их можно отсеять по ОДЗ для исходного уравнения. Но не всегда просто найти ОДЗ в виде числового множества. В таких случаях можно проводить отсеивание посторонних корней не по ОДЗ, а по условиям, определяющим ОДЗ. Разъясним, как проводится отсеивание посторонних корней по условиям ОДЗ.
Найденные корни по очереди подставляются в условия, определяющие ОДЗ для исходного уравнения или любого равносильного ему уравнения. Те из них, которые удовлетворяют всем условиям, являются корнями уравнения. А те из них, которые не удовлетворяют хотя бы одному условию или дают не имеющее смысла выражение, являются посторонними корнями для исходного уравнения.
Приведем пример отсеивания посторонних корней по условиям ОДЗ.
Решить иррациональное уравнение
Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
Понятно, что отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в одну и ту же четную степень, можно осуществить путем подстановки в исходное уравнение или в любое равносильное ему уравнение. Но такая проверка может быть связана со значительными вычислительными трудностями. На этот случай стоит знать альтернативный способ отсеивания посторонних корней, о котором мы сейчас и поговорим.
Отсеивание посторонних корней, которые могут возникнуть при возведении в одну и ту же четную степень обеих частей иррациональных уравнений вида 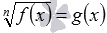
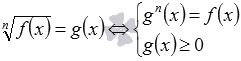
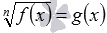
Покажем, как на практике отсеиваются посторонние корни указанным способом.
Решите уравнение
В заключение скажем, что рассмотренный подход является частным случаем более общего подхода к отсеиванию посторонних корней, возникающих при возведении обеих частей уравнения в одну и ту же четную степень. Отсеять посторонние корни, которые могут возникнуть при возведении обеих частей уравнения f(x)=g(x) в одну и ту же четную степень, можно по условию 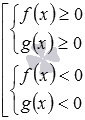
Приведем пример отсеивания посторонних корней предложенным способом. Возьмем уравнение 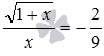
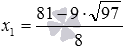

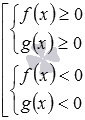
Подстановка в неравенство 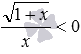
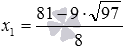
Полученное неравенство верное, так как в числителе положительное число, а в знаменателе – отрицательное, поэтому, отношение этих чисел есть отрицательное число. Значит, 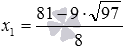
Подстановка в неравенство 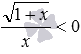

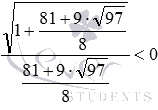

Видео:Учимся решать сложные логарифмические уравненияСкачать

Как решать логарифмические уравнения подробный разбор примеров
Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Сложение и вычитание логарифмов.
Возьмем два логарифма с одинаковыми основаниями: loga x и loga y. Тогда сними возможно выполнять операции сложения и вычитания:
Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов – логарифму частного. Причем это верно если числа а, х и у положительны и а ≠ 1.
Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!
Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.
Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а, x и у положительны и а ≠ 1, то:
Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а, х и у положительны и а ≠ 1, то:
Применим вышеизложенные теоремы для решения примеров:
Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:
так как выражения log2(-8) и log2(-4) вообще не определены (логарифмическая функция у = log2х определена лишь для положительных значений аргументах).
Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x1, x2, . . . ,xn существует тождество :
Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что loga1= 0, следовательно,
А значит имеет место равенство:
Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. 

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Два очевидных следствия определения логарифма
log a 1 = 0 ( a > 0, a ≠ 1 )
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.
Видео:Логарифмические уравнения 🥷🏿Скачать

Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 |  | ||||||||||||||
 |  | ||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | ( формула перехода к новому основанию логарифмов ), | ||||||||||||||
 | |||||||||||||||
 |
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать  Степень можно выносить за знак логарифмаИ вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример: log a ( f ( x ) 2 = 2 log a f ( x ) Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени. Видео:Логарифмическое уравнение / Как решить?Скачать  Логарифм произведения и логарифм частногоlog a b c = log a b − log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ. log a ( f ( x ) g ( x ) ) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля. Преобразуя данное выражение в сумму log a f ( x ) + log a g ( x ) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6). Видео:Логарифмические уравнения. Практическая часть. 11 класс.Скачать  Формула перехода к новому основаниюТот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной. Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8): log a b = 1 log b a ( a > 0, a ≠ 1, b > 0, b ≠ 1 ) Видео:Числовой логарифм. С корнем и в степени.Скачать  Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать: Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя! Видео:Логарифмические уравнения. Практическая часть. 11 класс.Скачать  Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор. Запомните, что логарифм от a по основанию а всегда равен единице: loga a = 1 – это логарифмическая единица. Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1: loga 1 = 0 – логарифмический ноль. Видео:Алгебра 10 класс (Урок№27 - Логарифмические уравнения.)Скачать  Как решать уравнения с логарифмами: 2 способа с примерамиРешить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида: При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку! Давайте посмотрим, как это работает на примере: Воспользуемся определением логарифма и получим: Теперь перед нами простейшее уравнение, решить которое не составит труда: Сделаем проверку. Подставим найденный Х в исходное уравнение: Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ. Поэтому мы покажем еще один способ решения логарифмических уравнений. Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так: Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере. Решим еще раз то же самое уравнение, но теперь этим способом: Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его: Воспользуемся этим свойством в нашем случае, получим: Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений. Разберем другой пример: Теперь делаем проверку: Еще один пример решения логарифмического уравнения:
Теперь подставим х2 = -5 в исходное уравнение: Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать  Сравнение логарифмов
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
|
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
| х 2 – 81 |
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| x = | x · y |
| y |
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений ∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^-6=left(x-3 right)^.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^=t), считают, что ( left(x-3 right)^=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^=t), тогда ( left(x-3 right)^=t^2) с продолжением:
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ = [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _xright)log _x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_sqrt+ 7log_x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
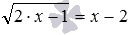
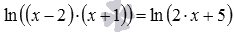
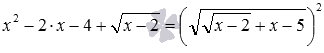
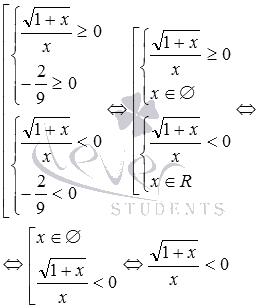
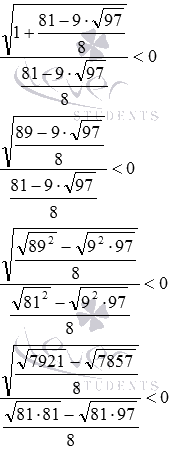

























 Логарифмы с одинаковыми основаниями можно вычитать:
Логарифмы с одинаковыми основаниями можно вычитать: 
 Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
 Вспоминаем определение логарифма и получаем следующее:
Вспоминаем определение логарифма и получаем следующее:  Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
 Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
 В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2. То есть в нашем случае:
То есть в нашем случае:  То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать: Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
 Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:
Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили: Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение: Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:  Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:  Теперь можно зачеркнуть логарифмы и тогда получим:
Теперь можно зачеркнуть логарифмы и тогда получим:  Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней:
Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней: то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
то последнее выражение верно. Следовательно, х = 3 является корнем уравнения. Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:  Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:  Выполнив преобразования правой и левой частей уравнения, мы получили:
Выполнив преобразования правой и левой частей уравнения, мы получили:  Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы: Решим данное квадратное уравнение, найдем дискриминант:
Решим данное квадратное уравнение, найдем дискриминант: Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Верно, следовательно, х1 = 1 является корнем уравнения.
Верно, следовательно, х1 = 1 является корнем уравнения. Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.










 Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.




 Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
 Применяем эти знания и получаем:
Применяем эти знания и получаем:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма: Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:
Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:  Делаем проверку:
Делаем проверку:  Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:
Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим: Верно, следовательно, х = 4 является корнем уравнения.
Верно, следовательно, х = 4 является корнем уравнения.
 Преобразуем правую часть уравнения:
Преобразуем правую часть уравнения:  Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:
Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:  Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы:  Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:


 Перепишем нашу систему:
Перепишем нашу систему:  Перепишем нашу систему: Следовательно, наша система примет следующий вид:
Перепишем нашу систему: Следовательно, наша система примет следующий вид:  Теперь решаем наше уравнение:
Теперь решаем наше уравнение:  Теперь решаем наше уравнение: Справа у нас квадрат суммы:
Теперь решаем наше уравнение: Справа у нас квадрат суммы: Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.





